目录
- 第二门课: 改善深层神经网络:超参数调试、正 则 化 以 及 优 化 (Improving Deep Neural Networks:Hyperparameter tuning, Regularization and Optimization)
- 第三周: 超 参 数 调 试 、 Batch 正 则 化 和 程 序 框 架(Hyperparameter tuning)
- 3.4 归一化网络的激活函数(Normalizing activations in a network)
- 3.5 将 Batch Norm 拟合进神经网络(Fitting Batch Norm into a neural network)
第二门课: 改善深层神经网络:超参数调试、正 则 化 以 及 优 化 (Improving Deep Neural Networks:Hyperparameter tuning, Regularization and Optimization)
第三周: 超 参 数 调 试 、 Batch 正 则 化 和 程 序 框 架(Hyperparameter tuning)
3.4 归一化网络的激活函数(Normalizing activations in a network)
在深度学习兴起后,最重要的一个思想是它的一种算法,叫做 Batch 归一化,由 Sergey loffe和Christian Szegedy 两位研究者创造。Batch归一化会使你的参数搜索问题变得很容易,使神经网络对超参数的选择更加稳定,超参数的范围会更加庞大,工作效果也很好,也会是你的训练更加容易,甚至是深层网络。让我们来看看 Batch 归一化是怎么起作用的吧。

当训练一个模型,比如 logistic 回归时,你也许会记得,归一化输入特征可以加快学习过程。你计算了平均值,从训练集中减去平均值,计算了方差,接着根据方差归一化你的数据集,在之前的视频中我们看到,这是如何把学习问题的轮廓,从很长的东西,变成更圆的东西,更易于算法优化。所以这是有效的,对 logistic 回归和神经网络的归一化输入特征值而言。
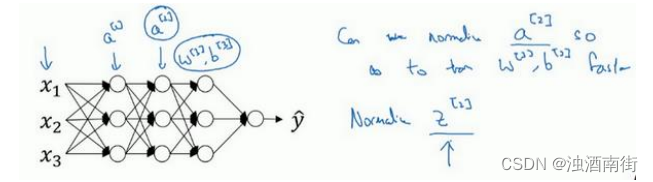
那么更深的模型呢?你不仅输入了特征值𝑥,而且这层有激活值
a
[
1
]
a^{[1]}
a[1],这层有激活值
a
[
2
]
a^{[2]}
a[2]等等。如果你想训练这些参数,比如
w
[
3
]
w^{[3]}
w[3],
b
[
3
]
b^{[3]}
b[3],那归一化
a
[
2
]
a^{[2]}
a[2]的平均值和方差岂不是很好?以便使
w
[
3
]
w^{[3]}
w[3],
b
[
3
]
b^{[3]}
b[3]的训练更有效率。在 logistic 回归的例子中,我们看到了如何归一化
x
1
x_1
x1,
x
2
x_2
x2,
x
3
x_3
x3,会帮助你更有效的训练w和b。
所以问题来了,对任何一个隐藏层而言,我们能否归一化a值,在此例中,比如说 a [ 2 ] a^{[2]} a[2]的值,但可以是任何隐藏层的,以更快的速度训练 w [ 3 ] w^{[3]} w[3], b [ 3 ] b^{[3]} b[3],因为 a [ 2 ] a^{[2]} a[2]是下一层的输入值,所以就会影响 w [ 3 ] w^{[3]} w[3], b [ 3 ] b^{[3]} b[3]的训练。简单来说,这就是 Batch 归一化的作用。尽管严格来说,我们真正归一化的不是 a [ 2 ] a^{[2]} a[2],而是 z [ 2 ] z^{[2]} z[2],深度学习文献中有一些争论,关于在激活函数之前是否应该将值 z [ 2 ] z^{[2]} z[2]归一化,或是否应该在应用激活函数 a [ 2 ] a^{[2]} a[2]后再规范值。实践中,经常做的是归一化 z [ 2 ] z^{[2]} z[2],所以这就是我介绍的版本,我推荐其为默认选择,那下面就是 Batch 归一化的使用方法。
在神经网络中,已知一些中间值,假设你有一些隐藏单元值,从
z
(
1
)
z^{(1)}
z(1)到
z
(
m
)
z^{(m)}
z(m),这些来源于隐藏层,所以这样写会更准确,
即
z
[
l
]
(
i
)
z^{[l](i)}
z[l](i)为隐藏层,𝑖从 1 到𝑚,但这样书写,我要省略𝑙及方括号,以便简化这一行的符号。所以已知这些值,如下,你要计算平均值,强调一下,所有这些都是针对𝑙层,但我省略𝑙及方括号,然后用正如你常用的那个公式计算方差,接着,你会取每个𝑧(𝑖)值,使其规范化,方法如下,减去均值再除以标准偏差,为了使数值稳定,通常将
ϵ
\epsilon
ϵ作为分母,以防防𝜎 = 0的情况。
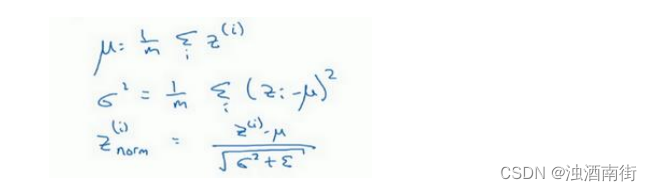
所以现在我们已把这些z值标准化,化为含平均值 0 和标准单位方差,所以𝑧的每一个分量都含有平均值 0 和方差 1,但我们不想让隐藏单元总是含有平均值 0 和方差 1,也许隐藏单元有了不同的分布会有意义,所以我们所要做的就是计算,我们称之为 z ^ ( i ) \hat{z}^{(i)} z^(i), z ^ ( i ) = γ z n o r m ( i ) + β \hat{z}^{(i)} = \gamma z_{norm}^{(i)} +\beta z^(i)=γznorm(i)+β,这里𝛾和𝛽是你模型的学习参数,所以我们使用梯度下降或一些其它类似梯度下降的算法,比如 Momentum 或者 Nesterov,Adam,你会更新𝛾和𝛽,正如更新神经网络的权重一样。
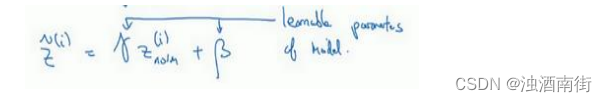
请注意𝛾和𝛽的作用是,你可以随意设置𝑧̃(𝑖)的平均值,事实上,如果
γ
=
σ
2
+
ϵ
\gamma = \sqrt{\sigma^2 + \epsilon}
γ=σ2+ϵ ,如果𝛾等于这个分母项(
z
n
o
r
m
(
i
)
=
z
(
i
)
−
μ
σ
2
+
ϵ
z_{norm}^{(i)} =\frac{z^{(i)} -\mu}{\sqrt{\sigma^2 + \epsilon}}
znorm(i)=σ2+ϵz(i)−μ中的分母),
β
\beta
β等于
μ
\mu
μ,这里的这个值是
z
n
o
r
m
(
i
)
=
z
(
i
)
−
μ
σ
2
+
ϵ
z_{norm}^{(i)} =\frac{z^{(i)} -\mu}{\sqrt{\sigma^2 + \epsilon}}
znorm(i)=σ2+ϵz(i)−μ中的
μ
\mu
μ,那么
γ
z
n
o
r
m
(
i
)
+
β
\gamma z_{norm}^{(i)} + \beta
γznorm(i)+β的作用在于,它会精确转化这个方程,如果这些成立(
γ
=
σ
2
+
ϵ
\gamma = \sqrt{\sigma^2 + \epsilon}
γ=σ2+ϵ,
β
=
μ
\beta =\mu
β=μ),那么
z
^
(
i
)
=
z
(
i
)
\hat{z}^{(i)} = z^{(i)}
z^(i)=z(i)。
通过对𝛾和𝛽合理设定,规范化过程,即这四个等式,从根本来说,只是计算恒等函数,通过赋予𝛾和𝛽其它值,可以使你构造含其它平均值和方差的隐藏单元值。

所以,在网络匹配这个单元的方式,之前可能是用 z ( 1 ) z^{(1)} z(1), z ( 2 ) z^{(2)} z(2)等等,现在则会用 z ^ i \hat{z}^{i} z^i取代 z ( i ) z^{(i)} z(i),方便神经网络中的后续计算。如果你想放回[𝑙],以清楚的表明它位于哪层,你可以把它放这。
所以我希望你学到的是,归一化输入特征X是怎样有助于神经网络中的学习,Batch 归一化的作用是它适用的归一化过程,不只是输入层,甚至同样适用于神经网络中的深度隐藏层。你应用 Batch 归一化了一些隐藏单元值中的平均值和方差,不过训练输入和这些隐藏单元值的一个区别是,你也许不想隐藏单元值必须是平均值 0 和方差 1。

比如,如果你有 sigmoid 激活函数,你不想让你的值总是全部集中在这里,你想使它们有更大的方差,或不是 0 的平均值,以便更好的利用非线性的 sigmoid 函数,而不是使所有的值都集中于这个线性版本中,这就是为什么有了𝛾和𝛽两个参数后,你可以确保所有的
z
(
i
)
z^{(i)}
z(i)值可以是你想赋予的任意值,或者它的作用是保证隐藏的单元已使均值和方差标准化。那里,均值和方差由两参数控制,即𝛾和𝛽,学习算法可以设置为任何值,所以它真正的作用是,使隐藏单元值的均值和方差标准化,即
z
(
i
)
z^{(i)}
z(i)有固定的均值和方差,均值和方差可以是 0 和 1,也可以是其它值,它是由𝛾和𝛽两参数控制的。
我希望你能学会怎样使用 Batch 归一化,至少就神经网络的单一层而言,在下一个视频中,我会教你如何将 Batch 归一化与神经网络甚至是深度神经网络相匹配。对于神经网络许多不同层而言,又该如何使它适用,之后,我会告诉你,Batch 归一化有助于训练神经网络的原因。所以如果觉得 Batch 归一化起作用的原因还显得有点神秘,那跟着我走,在接下来的两个视频中,我们会弄清楚。
3.5 将 Batch Norm 拟合进神经网络(Fitting Batch Norm into a neural network)
你已经看到那些等式,它可以在单一隐藏层进行 Batch 归一化,接下来,让我们看看它是怎样在深度网络训练中拟合的吧。

假设你有一个这样的神经网络,我之前说过,你可以认为每个单元负责计算两件事。第一,它先计算z,然后应用其到激活函数中再计算a,所以我可以认为,每个圆圈代表着两步的计算过程。同样的,对于下一层而言,那就是 z 1 [ 2 ] z_1^{[2]} z1[2]和 z 2 [ 2 ] z_2^{[2]} z2[2]等。所以如果你没有应用 Batch 归一化,你会把输入𝑋拟合到第一隐藏层,然后首先计算 z [ 1 ] z^{[1]} z[1],这是由 w [ 1 ] w^{[1]} w[1]和 b [ 1 ] b^{[1]} b[1]两个参数控制的。接着,通常而言,你会把 z [ 1 ] z^{[1]} z[1]拟合到激活函数以计算 a [ 1 ] a^{[1]} a[1]。但 Batch 归一化的做法是将 z [ 1 ] z^{[1]} z[1]值进行 Batch 归一化,简称 BN,此过程将由 β [ 1 ] \beta^{[1]} β[1]和 γ [ 1 ] \gamma^{[1]} γ[1]两参数控制,这一操作会给你一个新的规范化的 z [ 1 ] z^{[1]} z[1]值( z ^ [ 1 ] \hat{z}^[1] z^[1]),然后将其输入激活函数中得到 a [ 1 ] a^{[1]} a[1],即 a [ 1 ] = g [ 1 ] ( z ^ [ l ] ) a^{[1]} = g^{[1]}(\hat{z}^{[l]}) a[1]=g[1](z^[l])。
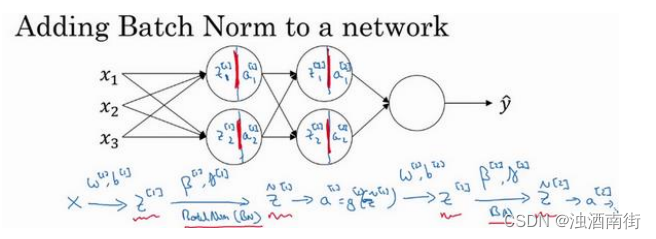
现在,你已在第一层进行了计算,此时 Batch 归一化发生在𝑧的计算和𝑎之间,接下来,你需要应用
a
[
1
]
a^{[1]}
a[1]值来计算
z
[
2
]
z^{[2]}
z[2],此过程是由
w
[
2
]
w^{[2]}
w[2]和
b
[
2
]
b^{[2]}
b[2]控制的。与你在第一层所做的类似,你会将
z
[
2
]
z^{[2]}
z[2]进行 Batch 归一化,现在我们简称 BN,这是由下一层的 Batch 归一化参数所管制的,即
β
[
2
]
\beta^{[2]}
β[2]和
γ
[
2
]
\gamma^{[2]}
γ[2],现在你得到
z
^
[
2
]
\hat{z}^{[2]}
z^[2],再通过激活函数计算出
a
[
2
]
a^{[2]}
a[2]等等。
所以需要强调的是 Batch 归一化是发生在计算𝑧和𝑎之间的。直觉就是,与其应用没有归一化的𝑧值,不如用归一过的 z ^ \hat{z} z^,这是第一层( z ^ [ 1 ] \hat{z}^{[1]} z^[1])。第二层同理,与其应用没有规范过的 z [ 2 ] z^{[2]} z[2]值,不如用经过方差和均值归一后的 z ^ [ 2 ] \hat{z}^{[2]} z^[2]。所以,你网络的参数就会是 w [ 1 ] w^{[1]} w[1], b [ 1 ] b^{[1]} b[1], w [ 2 ] w^{[2]} w[2]和 b [ 2 ] b^{[2]} b[2]等等,我们将要去掉这些参数。但现在,想象参数 w [ 1 ] w^{[1]} w[1], b [ 1 ] b^{[1]} b[1]到 w [ l ] w^{[l]} w[l], b [ l ] b^{[l]} b[l],我们将另一些参数加入到此新网络中 β [ 1 ] \beta^{[1]} β[1], β [ 2 ] \beta^{[2]} β[2], γ [ 1 ] \gamma^{[1]} γ[1], γ [ 2 ] \gamma^{[2]} γ[2]等等。对于应用 Batch 归一化的每一层而言。需要澄清的是,请注意,这里的这些 β \beta β( β [ 1 ] \beta^{[1]} β[1], β [ 2 ] \beta^{[2]} β[2]等等)和超参数 β \beta β没有任何关系,下一张幻灯片中会解释原因,后者是用于 Momentum 或计算各个指数的加权平均值。Adam 论文的作者,在论文里用 β \beta β代表超参数。Batch 归一化论文的作者,则使用 β \beta β代表此参数( β [ 1 ] \beta^{[1]} β[1], β [ 2 ] \beta^{[2]} β[2]等等),但这是两个完全不同的 β \beta β。我在两种情况下都决定使用 β \beta β,以便你阅读那些原创的论文,但 Batch 归一化学习参数 β [ 1 ] \beta^{[1]} β[1], β [ 2 ] \beta^{[2]} β[2]等等和用于 Momentum、Adam、RMSprop 算法中的𝛽不同。

所以现在,这是你算法的新参数,接下来你可以使用想用的任何一种优化算法,比如使用梯度下降法来执行它。
举个例子,对于给定层,你会计算 d β [ l ] d\beta^{[l]} dβ[l],接着更新参数 β \beta β为 β [ l ] \beta^{[l]} β[l] = β [ l ] \beta^{[l]} β[l] − α d β [ l ] \alpha d\beta^{[l]} αdβ[l]。你也可以使用 Adam 或 RMSprop 或 Momentum,以更新参数 β \beta β和𝛾,并不是只应用梯度下降法。
即使在之前的视频中,我已经解释过 Batch 归一化是怎么操作的,计算均值和方差,减去均值,再除以方差,如果它们使用的是深度学习编程框架,通常你不必自己把 Batch 归一化步骤应用于 Batch 归一化层。因此,探究框架,可写成一行代码,比如说,在 TensorFlow框架中,你可以用这个函数(tf.nn.batch_normalization)来实现 Batch 归一化,我们稍后讲解,但实践中,你不必自己操作所有这些具体的细节,但知道它是如何作用的,你可以更好的理解代码的作用。但在深度学习框架中,Batch 归一化的过程,经常是类似一行代码的东西。
所以,到目前为止,我们已经讲了 Batch 归一化,就像你在整个训练站点上训练一样,或就像你正在使用 Batch 梯度下降法。
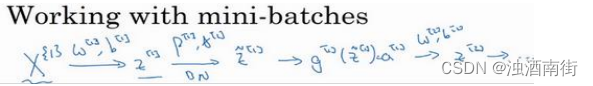
实践中,Batch 归一化通常和训练集的 mini-batch 一起使用。你应用 Batch 归一化的方式就是,你用第一个 mini-batch(X^{{1}}),然后计算 z [ 1 ] z^{[1]} z[1],这和上张幻灯片上我们所做的一样,应用参数 w [ 1 ] w^{[1]} w[1]和 b [ 1 ] b^{[1]} b[1],使用这个 m i n i − b a t c h ( X 1 ) mini-batch(X^{{1}}) mini−batch(X1)。接着,继续第二个 mini-batch(X^{{2}}),接着Batch 归一化会减去均值,除以标准差,由 β [ 1 ] \beta^{[1]} β[1]和 γ [ 1 ] \gamma^{[1]} γ[1]重新缩放,这样就得到了 z ^ [ 1 ] \hat{z}^{[1]} z^[1],而所有的这些都是在第一个 mini-batch 的基础上,你再应用激活函数得到 a [ 1 ] a^{[1]} a[1]。然后用 w [ 2 ] w^{[2]} w[2]和 b [ 2 ] b^{[2]} b[2]计算 z [ 2 ] z^{[2]} z[2],等等,所以你做的这一切都是为了在第一个 mini-batch( X 1 X^{{1}} X1)上进行一步梯度下降法。
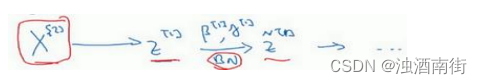
类似的工作,你会在第二个 mini-batch(KaTeX parse error: Expected 'EOF', got '}' at position 7: X^[{2}}̲)上计算
z
[
1
]
z^{[1]}
z[1],然后用 Batch 归一化来计算
z
^
[
1
]
\hat{z}^{[1]}
z^[1],所以 Batch 归一化的此步中,你用第二个 mini-batch(KaTeX parse error: Expected 'EOF', got '}' at position 7: X^[{2}}̲)中的数据使
z
^
[
1
]
\hat{z}^{[1]}
z^[1]归一化,这里的 Batch 归一化步骤也是如此,让我们来看看在第二个 mini-batch(
X
2
X^{{2}}
X2)中的例子,在mini-batch 上计算
z
[
1
]
z^{[1]}
z[1]的均值和方差,重新缩放的
β
\beta
β和
γ
\gamma
γ得到
z
[
1
]
z^{[1]}
z[1],等等。
然后在第三个 mini-batch( X 3 X^{{3}} X3)上同样这样做,继续训练。
现在,我想澄清此参数的一个细节。先前我说过每层的参数是 w [ l ] w^{[l]} w[l]和 b [ l ] b^{[l]} b[l],还有 β [ l ] \beta^{[l]} β[l]和 γ [ l ] \gamma^{[l]} γ[l],请注意计算𝑧的方式如下, z [ l ] z^{[l]} z[l] = w [ l ] a [ l − 1 ] + b [ l ] w^{[l]}a^{[l−1]} + b^{[l]} w[l]a[l−1]+b[l],但 Batch 归一化做的是,它要看这个 mini-batch,先将 z [ l ] z^{[l]} z[l]归一化,结果为均值 0 和标准方差,再由 β \beta β和 γ \gamma γ重缩放,但这意味着,无论 b [ l ] b^{[l]} b[l]的值是多少,都是要被减去的,因为在 Batch 归一化的过程中,你要计算 z [ l ] z^{[l]} z[l]的均值,再减去平均值,在此例中的 mini-batch 中增加任何常数,数值都不会改变,因为加上的任何常数都将会被均值减去所抵消。
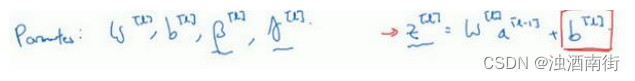
所以,如果你在使用 Batch 归一化,其实你可以消除这个参数( b [ l ] b^{[l]} b[l]),或者你也可以,暂时把它设置为 0,那么,参数变成 z [ l ] z^{[l]} z[l] = w [ l ] a [ l − 1 ] w^{[l]}a^{[l−1]} w[l]a[l−1],然后你计算归一化的 z [ l ] z^{[l]} z[l], z ^ [ l ] \hat{z}^{[l]} z^[l] = γ [ l ] \gamma^{[l]} γ[l] z [ l ] z^{[l]} z[l]+ β [ l ] \beta^{[l]} β[l],你最后会用参数 β [ l ] \beta^{[l]} β[l],以便决定 z ^ [ l ] \hat{z}^{[l]} z^[l]的取值,这就是原因。

所以总结一下,因为 Batch 归一化超过了此层
z
[
l
]
z^{[l]}
z[l]的均值,𝑏[𝑙]这个参数没有意义,所以,你必须去掉它,由
β
[
l
]
\beta^{[l]}
β[l]代替,这是个控制参数,会影响转移或偏置条件。
最后,请记住 z [ l ] z^{[l]} z[l]的维数,因为在这个例子中,维数会是( n [ l ] n^{[l]} n[l], 1), β [ l ] \beta^{[l]} β[l]的尺寸为( n [ l ] n^{[l]} n[l], 1),如果是 l 层隐藏单元的数量,那 β [ l ] \beta^{[l]} β[l]和 γ [ l ] \gamma^{[l]} γ[l]的维度也是( n [ l ] n^{[l]} n[l], 1),因为这是你隐藏层的数量,你有 n [ l ] n^{[l]} n[l]隐藏单元,所以 β [ l ] \beta^{[l]} β[l]和 γ [ l ] \gamma^{[l]} γ[l]用来将每个隐藏层的均值和方差缩放为网络想要的值。

让我们总结一下关于如何用 Batch 归一化来应用梯度下降法,假设你在使用 mini-batch梯度下降法,你运行𝑡 = 1到 batch 数量的 for 循环,你会在 mini-batch
X
t
X^{{t}}
Xt上应用正向 prop,每个隐藏层都应用正向 prop,用 Batch 归一化代替
z
[
l
]
z^{[l]}
z[l]为
z
^
[
l
]
\hat{z}^{[l]}
z^[l]。接下来,它确保在这个 mini-batch 中,𝑧值有归一化的均值和方差,归一化均值和方差后是
z
^
[
l
]
\hat{z}^{[l]}
z^[l],然后,你用反向 prop 计算
d
w
[
l
]
dw^{[l]}
dw[l]和
d
b
[
l
]
db^{[l]}
db[l],及所有 l 层所有的参数,
d
β
[
l
]
d\beta^{[l]}
dβ[l]和
d
γ
[
l
]
d\gamma^{[l]}
dγ[l]。尽管严格来说,因为你要去掉𝑏,这部分其实已经去掉了。最后,你更新这些参数:
w
[
l
]
w^{[l]}
w[l]=
w
[
l
]
−
α
d
w
[
l
]
w^{[l]} − \alpha dw^{[l]}
w[l]−αdw[l],和以前一样,
β
[
l
]
\beta^{[l]}
β[l]=
β
[
l
]
−
α
d
β
[
l
]
\beta^{[l]} −\alpha d\beta^{[l]}
β[l]−αdβ[l],对于𝛾也是如此
γ
[
l
]
\gamma^{[l]}
γ[l]=
γ
[
l
]
−
α
d
γ
[
l
]
\gamma^{[l]} − \alpha d\gamma^{[l]}
γ[l]−αdγ[l]。
如果你已将梯度计算如下,你就可以使用梯度下降法了,这就是我写到这里的,但也适用于有 Momentum、RMSprop、Adam 的梯度下降法。与其使用梯度下降法更新 mini-batch,你可以使用这些其它算法来更新,我们在之前几个星期中的视频中讨论过的,也可以应用其它的一些优化算法来更新由 Batch 归一化添加到算法中的 β \beta β 和 γ \gamma γ参数。

我希望,你能学会如何从头开始应用 Batch 归一化,如果你想的话。如果你使用深度学习编程框架之一,我们之后会谈。希望,你可以直接调用别人的编程框架,这会使 Batch归一化的使用变得很容易。
现在,以防 Batch 归一化仍然看起来有些神秘,尤其是你还不清楚为什么其能如此显著的加速训练,我们进入下一个视频,详细讨论 Batch 归一化为何效果如此显著,它到底在做什么。