目录

1.素数回文

2.活动安排

3.合唱团

---

1.素数回文

链接https://www.nowcoder.com/practice/d638855898fb4d22bc0ae9314fed956f?tpId=290&tqId=39945&ru=/exam/oj

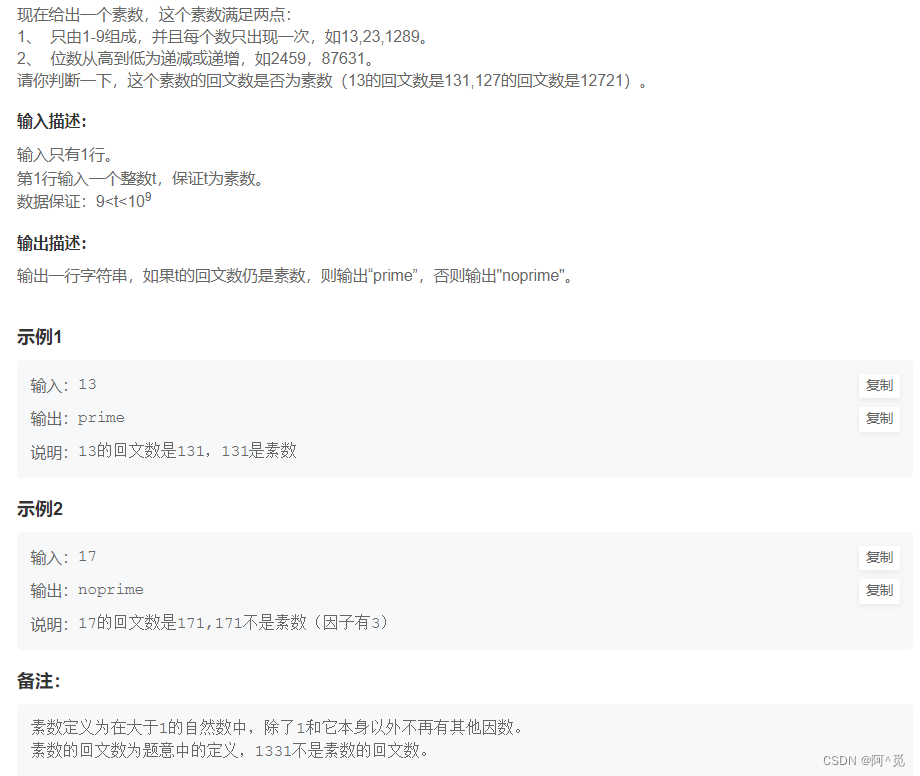
现将其转化为回文数（这里用字符串存储比较方便转化），然后判断是否为素数即可。

stoi函数一定要自己写，库里面的stoi不支持大数据转化，会越界

#include <iostream>
using namespace std;
#define int long long
bool Check(int x)
{
	if (x < 2)
		return false;
	for (int i = 2; i * i <= x; ++i)
		if (x % i == 0)
			return false;
	return true;
}

int my_stoi(string s)
{
	int sum = 0;
	for (int i = s.size() - 1; i >= 0; --i)
		sum = sum * 10 + (s[i] - '0');
	return sum;
}

signed main() {
	string s;
	cin >> s;
	int n = s.size();
	for (int i = n - 2; i >= 0; --i)
		s += s[i];
	int tmp = my_stoi(s);
	if (Check(tmp))
		cout << "prime" << endl;
	else
		cout << "noprime" << endl;
	return 0;
}

2.活动安排

链接https://www.nowcoder.com/practice/16d971e9e42e4f3b9b1e2b8794796a43?tpId=308&tqId=40488&ru=/exam/oj

做一个简单的规划即可：

end存储为目前多久结束活动。

先将活动的开始时间进行排序

然后若 i 的开始时间小于 end，则更新end = min（end，i的结束时间），{取最小值的原因是贪心（要选择尽可能多的活动数量）}

若 i 的开始时间大于或等于 end，直接让活动数 +1。

#include <iostream>
#include <utility>
#include <algorithm>
using namespace std;

typedef pair<int, int> PII;
const int N = 2e5 + 10;
int n;
PII a[N];

int main() {
	cin >> n;
	for (int i = 0; i < n; ++i)
		cin >> a[i].first >> a[i].second;

	sort(a, a + n);
	int ret = 1;
	int end = a[0].second;
	for (int i = 1; i < n; ++i)
	{
		if (a[i].first < end)
		{
			end = min(end, a[i].second);
		}
		else
		{
			ret++;
			end = a[i].second;
		}
	}
	cout << ret << endl;
	return 0;
}

3.合唱团

链接https://www.nowcoder.com/practice/661c49118ca241909add3a11c96408c8?tpId=122&tqId=33652&ru=/exam/oj

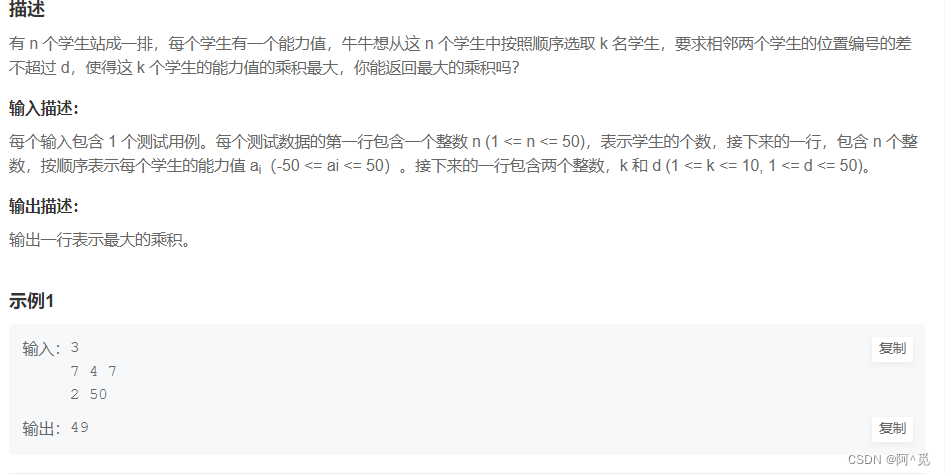
一个巨型复杂的dp问题：

若搞清楚了该题的状态表示，还是可以做一下题目的。

因为状态表示是最后一个人必须，所以我们选取返回值时，需要遍历一遍从 k 到 n。

即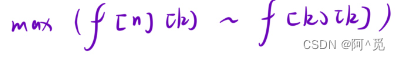

很细节的一个地方是他的初始化，因为你不确定有没有负数，若是默认初始化（0），则会导致一个全为负数的数组中返回 0 ，这样是答案错误。

因此我们可以边填表边初始化。

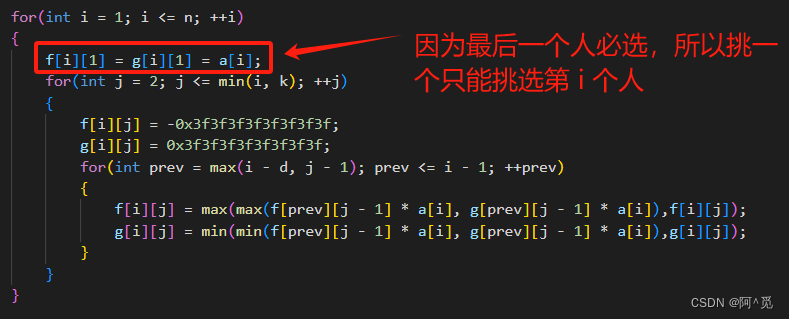
初始化为最小和最大：

#include <iostream>
using namespace std;
#define int long long

const int N = 55, M = 15;
int f[N][M];
int g[N][M];
int a[N];
int n, k, d;

signed main() {
    cin >> n;
    for(int i = 1; i <= n; ++i)
        cin >> a[i];
    cin >> k >> d;

    for(int i = 1; i <= n; ++i)
    {
        f[i][1] = g[i][1] = a[i];
        for(int j = 2; j <= min(i, k); ++j)
        {
            f[i][j] = -0x3f3f3f3f3f3f3f3f;
            g[i][j] = 0x3f3f3f3f3f3f3f3f;
            for(int prev = max(i - d, j - 1); prev <= i - 1; ++prev)
            {
                f[i][j] = max(max(f[prev][j - 1] * a[i], g[prev][j - 1] * a[i]),f[i][j]);
                g[i][j] = min(min(f[prev][j - 1] * a[i], g[prev][j - 1] * a[i]),g[i][j]);               
            }
        }
    }

    int ret = -0x3f3f3f3f3f3f3f3f;
    for(int i = k; i <= n; ++i)
        ret = max(ret, f[i][k]);
    cout << ret << endl;
    return 0;
}