博主主页: 码农派大星.

关注博主带你了解更多数据结构知识

---

1.非递归的前序遍历

1.用栈来实现

2,前序遍历是根左右, 先是根节点入栈,,然后不为空时向左遍历,当为空时就返回向右遍历,右为空时直接出栈,依次循环即可.

public void preOrderNot(TreeNode root){
        Stack<TreeNode> stack = new Stack<>();
         if(root==null){
            return;
        }
        TreeNode cur = root;

        while (cur != null || !stack.isEmpty()){
            while (cur != null){
                stack.push(cur);
                System.out.print(cur.val + " ");
                cur = cur.left;
            }
            TreeNode top = stack.pop();
            cur = top.right;
        }
    }

2.非递归的中序遍历

1和前序遍历不同的是,中序遍历是左根右

2先让左节点入栈,一直往左遍历,直到遇到空时,返回根节点,再向右一直遍历,遇到右为空时,出栈.

public void inOrderNot(TreeNode root) {
        Stack<TreeNode> stack = new Stack<>();
        if(root==null){
            return;
        }
        TreeNode cur = root;
        while (cur != null || !stack.isEmpty()) {
            while (cur != null) {
                stack.push(cur);
                cur = cur.left;
            }
            TreeNode top = stack.pop();
            System.out.print(top.val + " ");
            cur = top.right;
        }
    }

3.非递归的后序遍历

后序遍历是左右根,我们先让左节点入栈,再一直向左遍历,当为空的时候需要peek一下判断右节点是否为空，如果右节点为空则出栈，如果右节点不为空那么遍历右节点.

注意:

当右节点不为空遍历右节点的时候，可能造成死循环，所以我们需要定义一个prev值来表示最后一个被打印的节点。

 public void PostOrderNot(TreeNode root) {
        Stack<TreeNode> stack = new Stack<>();
        TreeNode cur = root;
        TreeNode prev = null;
        while (cur != null || !stack.isEmpty()) {
            while (cur != null) {
                stack.push(cur);
                cur = cur.left;
            }
            TreeNode top = stack.peek();
            if (top.right == null || top.right == prev) {
                //打印当前top 并弹出
                stack.pop();
                System.out.print(top.val + " ");
                prev = top;
            } else {
                cur = top.right;
            }
}

4.根据二叉树创建字符串OJ链接

给你二叉树的根节点 root ，请你采用前序遍历的方式，将二叉树转化为一个由括号和整数组成的字符串，返回构造出的字符串。

空节点使用一对空括号对 "()" 表示，转化后需要省略所有不影响字符串与原始二叉树之间的一对一映射关系的空括号对。

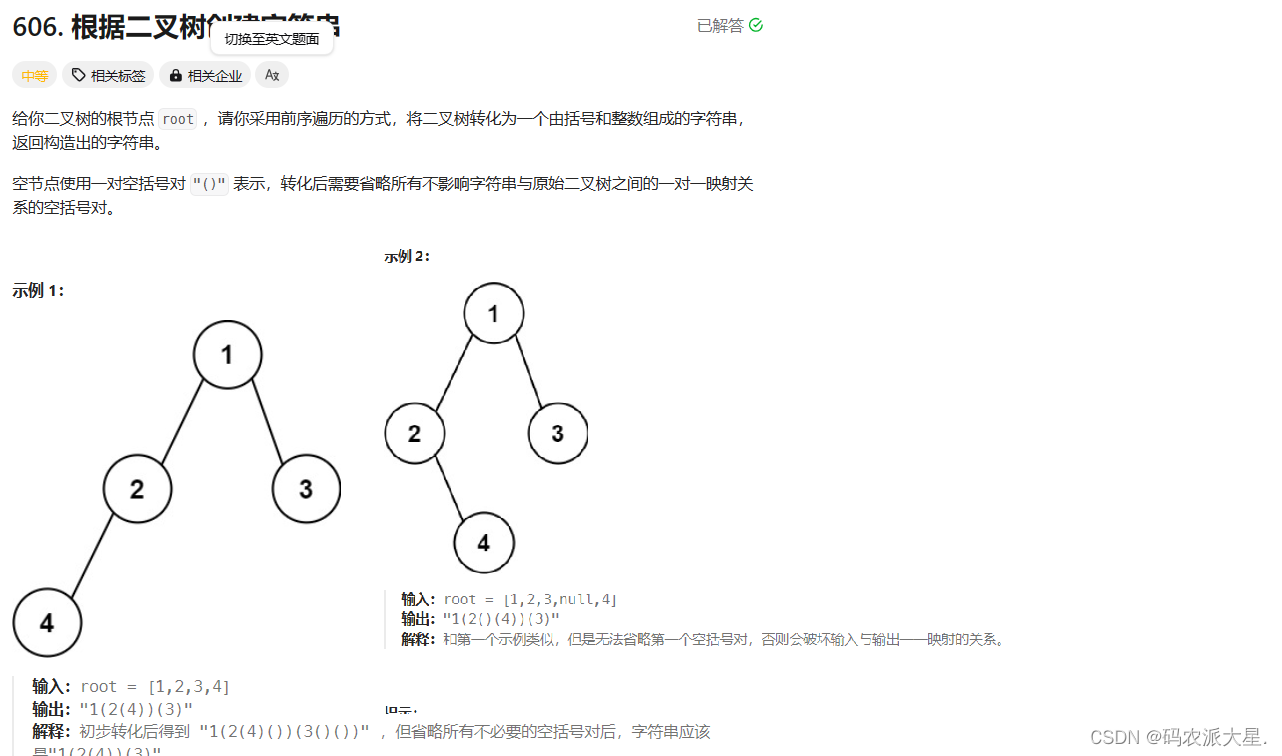
解题:先遍历左 如果左不为空为(root.left),如果为空,判断右是否为空,如果为空(就是左右都为空)什么都不返回,不为空返回()

再处理右树,如果为空什么都不返回,如果不为空返回(root.right)

class Solution {
    public String tree2str(TreeNode root) {
        StringBuilder stringBuilder = new StringBuilder();
        tree2strChild(root,stringBuilder);
        return stringBuilder.toString();
    }
    private void tree2strChild(TreeNode root,StringBuilder stringBuilder){
        if(root == null)return;
        stringBuilder.append(root.val);
        if(root.left != null){
            stringBuilder.append("(");
            tree2strChild(root.left,stringBuilder);
            stringBuilder.append(")");
        }else{
            //左边为空 右也为空
            if(root.right == null){
                return;
            }else{
                stringBuilder.append("()");
            }
        }
        //处理root右树情况
        if(root.right == null){
            return;
        }else{
            stringBuilder.append("(");
            tree2strChild(root.right,stringBuilder);
            stringBuilder.append(")");
        }      
    }
}

 5.根据一棵树的前序遍历与中序遍历构造二叉树OJ链接

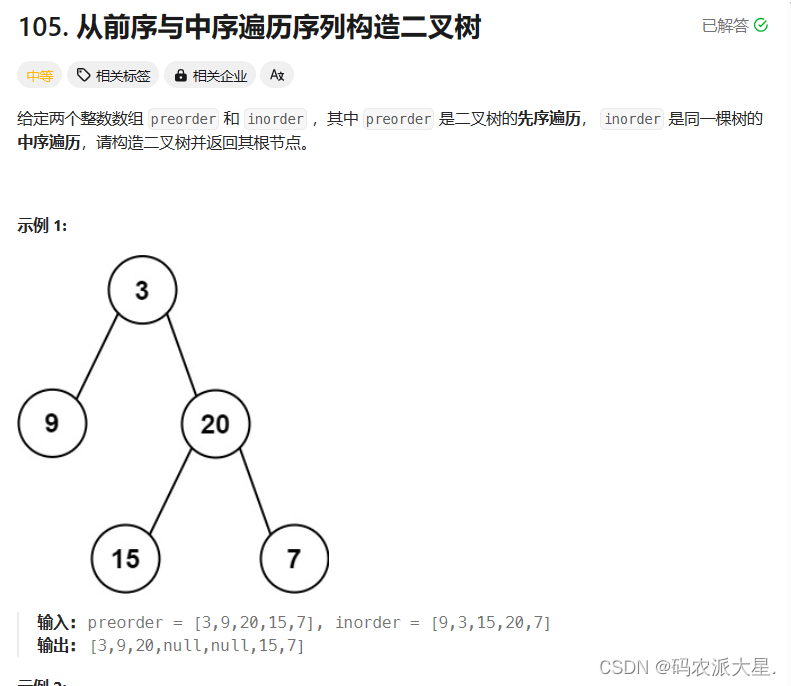
class Solution {
    public int preIndex;
    public TreeNode buildTree(int[] preorder, int[] inorder) {
    return buildTreeChilde(preorder,inorder,0,inorder.length-1);   
    }
 private TreeNode buildTreeChilde(int[] preorder,int[] inorder,int inBegin,int inEnd){
        if(inBegin > inEnd){
            return null;
        }        
        TreeNode root = new TreeNode(preorder[preIndex]);
        int rootIndex = findRootIndex(inorder,inBegin,inEnd,preorder[preIndex]);  
        preIndex++;
        root.left = buildTreeChilde(preorder,inorder,inBegin,rootIndex-1);
        root.right = buildTreeChilde(preorder,inorder,rootIndex+1,inEnd);
        return root;
    }
    private int findRootIndex(int[] inorder,int inBegin,int inEnd,int Key){
        for(int i = inBegin; i<= inEnd;i++){
            if(inorder[i] == Key){
                return i;
            }
        }
        return -1;
    }
}

 6.根据一棵树的中序遍历与后序遍历构造二叉树OJ链接

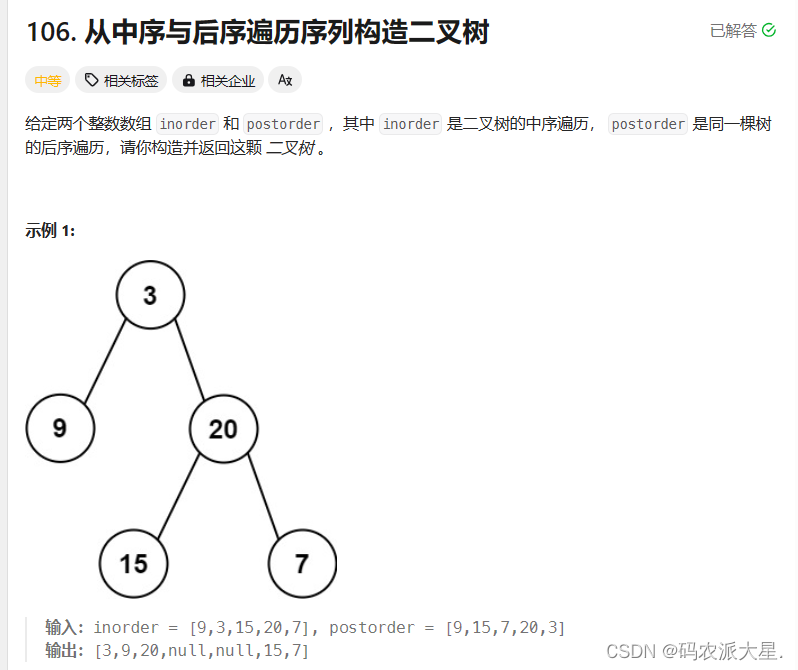
class Solution {
    public int  postIndex = 0;
    public TreeNode buildTree(int[] inorder, int[] postorder) {
        postIndex = postorder.length-1;
        return buildTreeChild(inorder,postorder,0,inorder.length-1);
    }
 private TreeNode buildTreeChild(int[] inorder,int[] postorder,int inBegin,int inEnd){
        if(inBegin > inEnd){
            return null;
        }
        TreeNode root = new TreeNode(postorder[postIndex]);
       int rootIndex = findRootIndex(inorder,inBegin, inEnd,postorder[postIndex]);
        postIndex--;
        root.right = buildTreeChild(inorder,postorder,rootIndex+1,inEnd);
        root.left = buildTreeChild(inorder,postorder,inBegin,rootIndex-1);
        return root;
    }
     private int findRootIndex(int[] inorder,int inBegin,int inEnd,int Key){
        for(int i = inBegin; i<= inEnd;i++){
            if(inorder[i] == Key){
                return i;
            }
        }
        return -1;
    }
}