参考论文

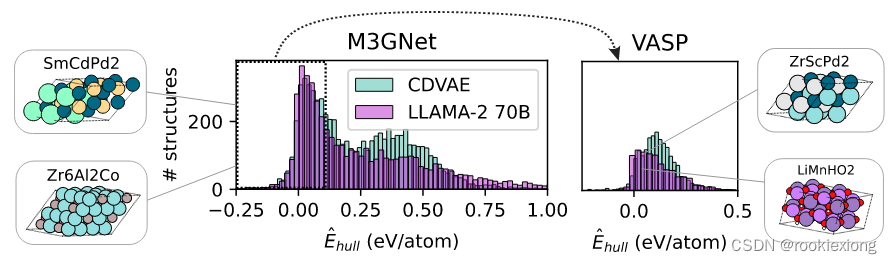
基于二进制文件的 C 语言编译器特征提取及识别

本实验使用 B2M 算法将可执行文件转为灰度图像，可执行文件转为灰度图的流程如图 4-3 所示。将 可执行文件每 8 位读取为一个无符号的的整型常量，一个可执行文件得到一个一维向量， 之后按照固定的宽和高将一维向量转成一个二维向量。该二维向量中每个元素的取值范围都在 0-255 ，正好对应灰度图像的一个像素点，将该二维数组可视化为一张灰度图像， 其中 0 表示黑色， 255 表示白色。

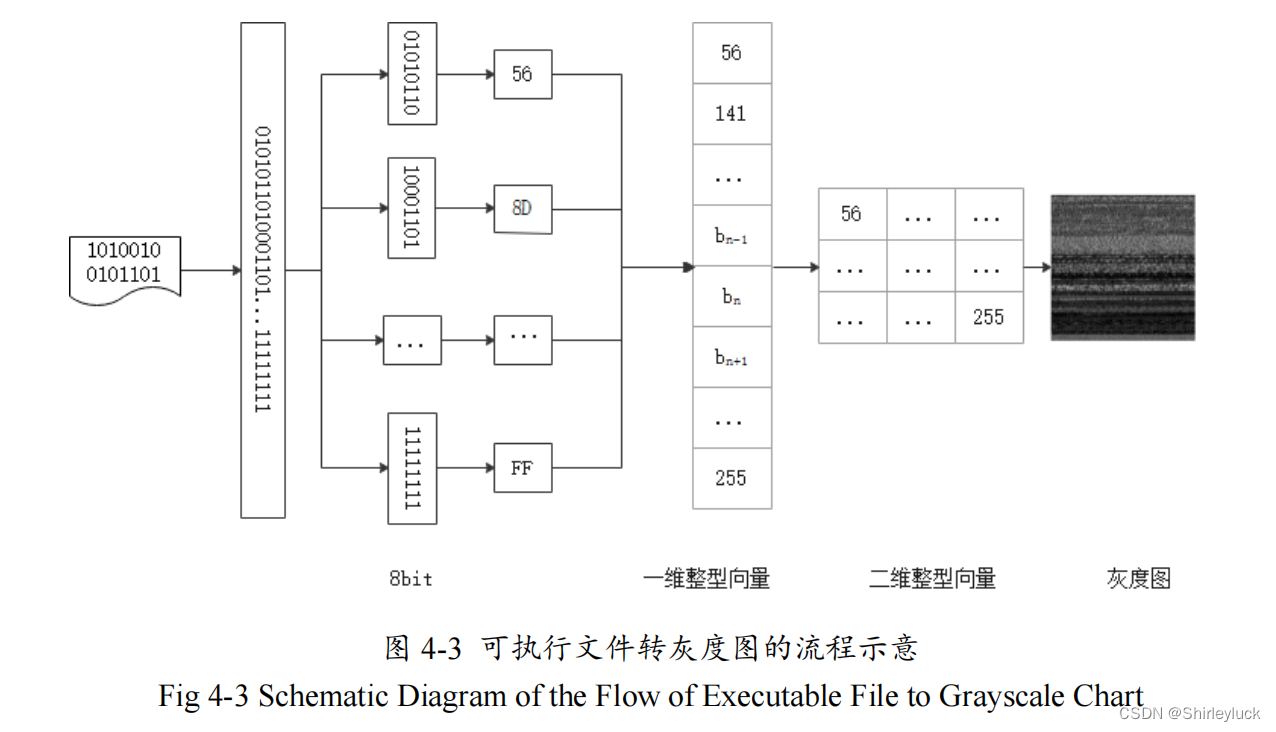
这个使用B2M 算法将可执行文件转为灰度图像的步骤主要视为了进行之后提取 GLCM 特征和 LBP 特征。

其中，生成图像的宽度会因不同文件的大小有最优宽度

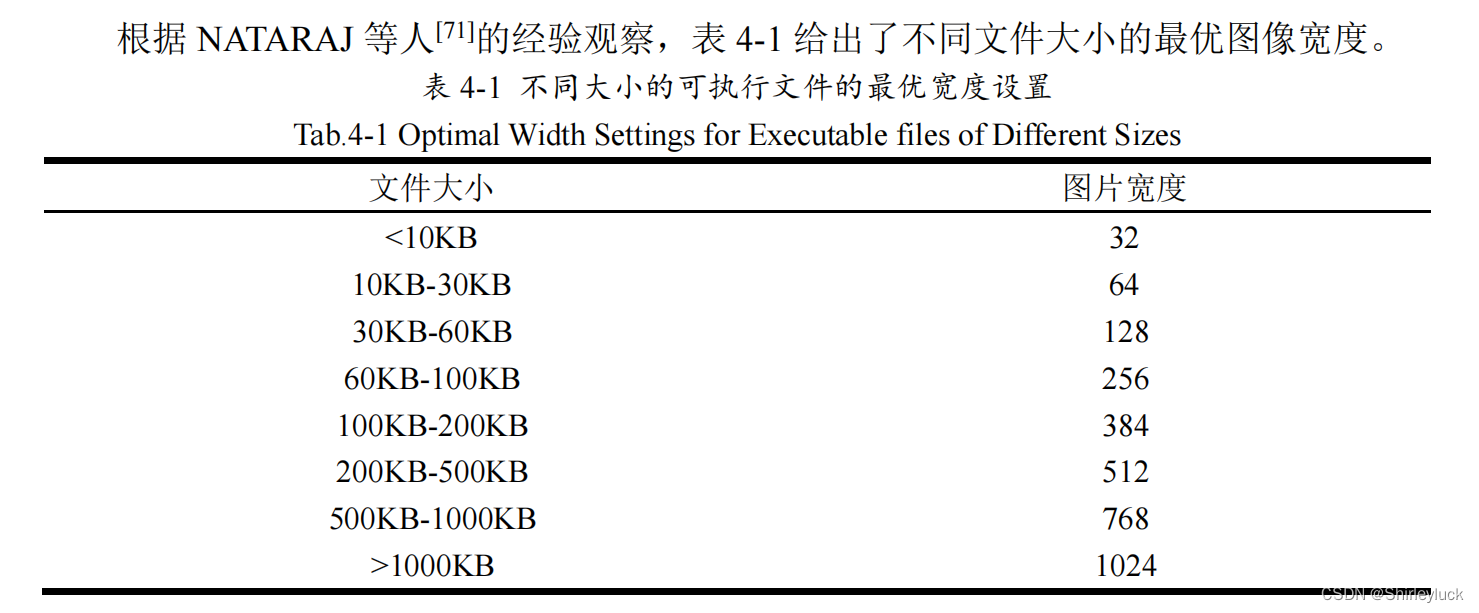
 示例：

我的exe文件大小事135kb所以宽度就设置成384了。

import numpy as np
import matplotlib.pyplot as plt

# 读取二进制文件
def read_binary_file(filename):
    with open(filename, 'rb') as f:
        data = f.read()
    return data

# 将数据转换为无符号整型数组
def binary_to_uint8_array(data):
    return np.frombuffer(data, dtype=np.uint8)

# 将一维数组转换为二维矩阵
def array_to_2d_matrix(array, width):
    # 计算高度
    height = int(np.ceil(len(array) / width))
    # 如果数组长度不是宽度的整数倍，填充数组
    padded_length = height * width
    padded_array = np.pad(array, (0, padded_length - len(array)), 'constant', constant_values=0)
    # 转换为二维矩阵
    matrix = padded_array.reshape((height, width))
    return matrix

# 保存灰度图像
def save_gray_image(matrix, save_path):
    plt.imshow(matrix, cmap='gray', vmin=0, vmax=255)
    plt.title("Gray Image")
    plt.axis('off')  # 隐藏坐标轴
    plt.savefig(save_path, bbox_inches='tight', pad_inches=0)
    plt.close()
    print(f"Image saved at {save_path}")

# 主函数
def binary_to_image(filename, save_path, width):
    data = read_binary_file(filename)
    uint8_array = binary_to_uint8_array(data)
    matrix = array_to_2d_matrix(uint8_array, width)
    save_gray_image(matrix, save_path)

# 调用主函数并传入二进制文件名、保存路径和宽度
binary_to_image('math1111.exe', 'test2.png', width=384)

生成的图像：

5.21

本来的程序是处理单张图片，现在需要处理比较多，所以把程序拓展到了处理整个文件夹中的exe文件，并把处理后的图片以原exe文件＋ 特殊备注（看个人需求）放到同一文件夹。同时根据原来exe文件的大小设置图片的宽度。

 

import os
import numpy as np
import matplotlib.pyplot as plt

# 读取二进制文件
def read_binary_file(filename):
    with open(filename, 'rb') as f:
        data = f.read()
    return data

# 将数据转换为无符号整型数组
def binary_to_uint8_array(data):
    return np.frombuffer(data, dtype=np.uint8)

# 将一维数组转换为二维矩阵
def array_to_2d_matrix(array, width):
    # 计算高度
    height = int(np.ceil(len(array) / width))
    # 如果数组长度不是宽度的整数倍，填充数组
    padded_length = height * width
    padded_array = np.pad(array, (0, padded_length - len(array)), 'constant', constant_values=0)
    # 转换为二维矩阵
    matrix = padded_array.reshape((height, width))
    return matrix

# 保存灰度图像
def save_gray_image(matrix, save_path):
    plt.imshow(matrix, cmap='gray', vmin=0, vmax=255)
    plt.title("Gray Image")
    plt.axis('off')  # 隐藏坐标轴
    plt.savefig(save_path, bbox_inches='tight', pad_inches=0)
    plt.close()
    print(f"Image saved at {save_path}")

# 处理单个文件并保存图像
def binary_to_image(filename, save_path, width):
    data = read_binary_file(filename)
    uint8_array = binary_to_uint8_array(data)
    matrix = array_to_2d_matrix(uint8_array, width)
    save_gray_image(matrix, save_path)

# 根据文件大小确定图像宽度
def determine_width(file_size):
    if file_size < 10 * 1024:
        return 32
    elif file_size < 30 * 1024:
        return 64
    elif file_size < 60 * 1024:
        return 128
    elif file_size < 100 * 1024:
        return 256
    elif file_size < 200 * 1024:
        return 384
    elif file_size < 500 * 1024:
        return 512
    elif file_size < 1000 * 1024:
        return 768
    else:
        return 1024

# 处理文件夹中的所有文件
def process_folder(folder_path, save_dir):
    if not os.path.exists(save_dir):
        os.makedirs(save_dir)
    for filename in os.listdir(folder_path):
        file_path = os.path.join(folder_path, filename)
        if os.path.isfile(file_path):  # 只处理文件，忽略子目录
            file_size = os.path.getsize(file_path)
            width = determine_width(file_size)
            base_name = os.path.splitext(os.path.basename(file_path))[0]
            new_name = f"{base_name}_10.3.0.png"
            save_path = os.path.join(save_dir, new_name)
            binary_to_image(file_path, save_path, width)

# 文件夹路径
folder_path = r'C:\Users\19427\Desktop\5.1.0'
save_directory = r'C:\Users\19427\Desktop\5.1.0\output_images'

# 调用函数处理文件夹
process_folder(folder_path, save_directory)