题目：

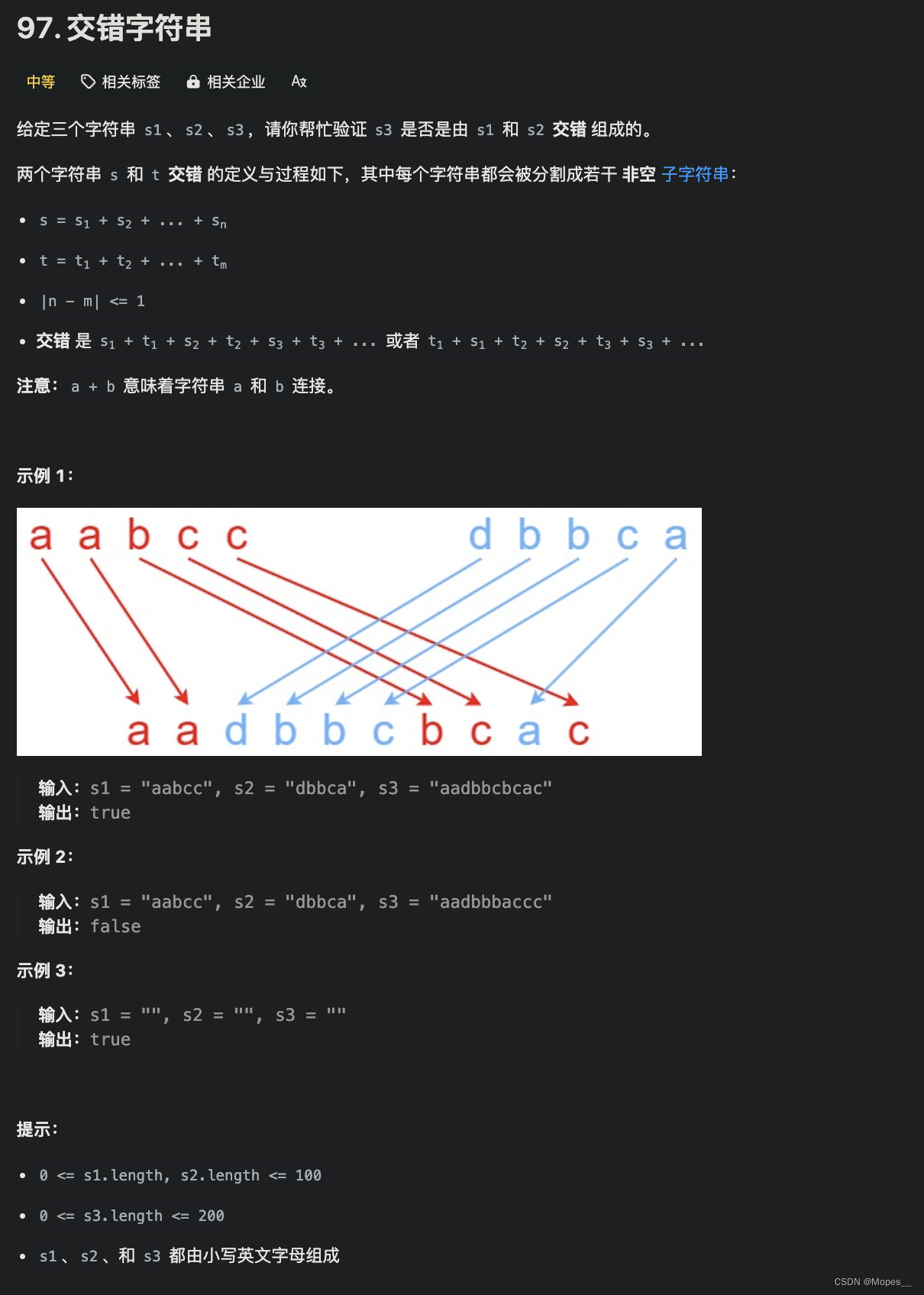
题解：

class Solution:
    def isInterleave(self, s1: str, s2: str, s3: str) -> bool:
        n1 = len(s1)
        n2 = len(s2)
        if len(s3) != n1 + n2: return False
        dp = [[False] * (n2 + 1) for _ in range(n1 + 1)]  # dp[i][j]表示s1[0:i)和s2[0:j)是否能够构成s3[0:i+j)
        # 边界处理
        dp[0][0] = True    
        for j in range(1, n2 + 1):
            dp[0][j] = dp[0][j-1] and (s2[j-1] == s3[j-1])  # 首行数据，i=0时s1[0:0)为空字符串；判断由仅由s2[0:j)是否可构s3[0:j)
        for i in range(1, n1 + 1):
            dp[i][0] = dp[i-1][0] and (s1[i-1] == s3[i-1])  # 首列数据，j=0时s2[0:0)为空字符串；判断由仅由s1[0:i)是否可构s3[0:i)
        # 状态转移：dp[i][j] = (dp[i-1][j] && s1[i-1] == s3[i+j-1]) || (dp[i][j - 1] && s2[j-1] == s3[i+j-1])
        for i in range(1, n1 + 1):
            for j in range(1, n2 + 1):
                # dp[i][j]状态转移，看新的字符s3[i+j-1]是否能够与s1或s2对应的字符匹配
                # 如果s1提供这个新字符s1[i-1]，就要看dp[i-1][j]示s1[0:i-1)和s2[0:j)是否能够构成s3[0:i+j-1)
                # 如果s2提供这个新字符s2[j-1]，就要看dp[i][j-1]示s1[0:i)和s2[0:j-1)是否能够构成s3[0:i+j-1)
                p = i + j - 1
                dp[i][j] = (dp[i-1][j] and s1[i-1] == s3[p]) or (dp[i][j - 1] and s2[j-1] == s3[p])
        return dp[n1][n2]