2.14 弹性网（Elastic Net）

Elastic Net是一种使用L1和L2作为正则化矩阵的线性回归模型，这种组合用于只有很少的权重非零的稀疏模型。
当多个特征和另一个特征相关时，弹性网络非常有用，Lasso倾向于随机选择其中一个，而弹性网络更倾向于选择两个。
在实践中，Lasso和Ridge之间权衡的一个优势是它允许在循环过程中继承了Ridge的稳定性。

1.代价函数：

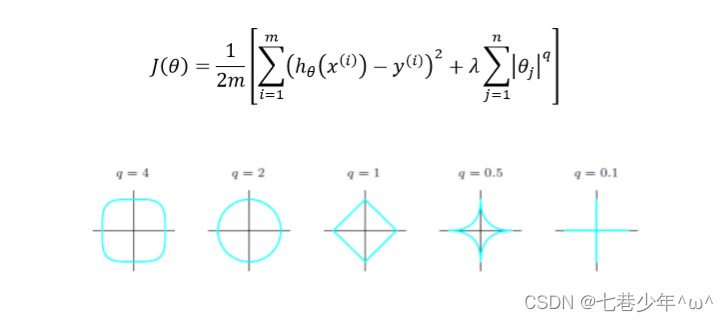
在这里插入图片描述

q=2时，岭回归，q=1时，LASSO回归，q不同所对应的图像不同，常用的是q=1或q=2
q值不同所对应的图像不同，常用的是q=1，q=2

2.弹性网中正则项的完整形式：

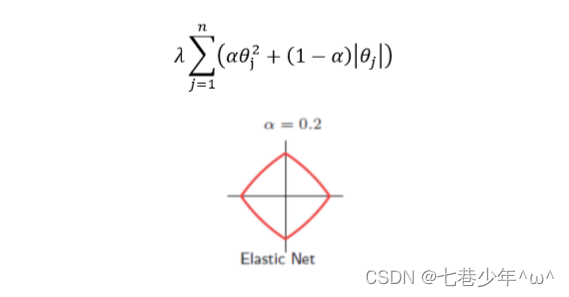
在这里插入图片描述

弹性网结合了岭回归和LASSO的特点，结果更精准一点
当α=0.2时，岭回归占0.2，LASSO占0.8

3.实战2：sklearn—弹性网：

1).CSV中的数据：

longley.csv

2).代码

import numpy as np
from numpy import genfromtxt
from sklearn import linear_model

# 导入数据
data = genfromtxt('D:\\Data\\longley.csv', delimiter=',')

# 数据切片
x_data = data[1:, 2:]
y_data = data[1:, 1]

# 加载模型
model = linear_model.ElasticNetCV()

# 拟合线性模型
model.fit(x_data, y_data)

# 弹性网系数
coeff = model.alpha_
print('弹性网系数:', coeff)

# 相关系数
rcoeff = model.coef_
print('相关系数:', rcoeff)

# 预测值
pred = model.predict(x_data[2, np.newaxis])
print('第二行的预测数据:', pred, '实际数据:88.2')