一、拟合度概念
在所有的模型优化问题中,最基础的也是最核心的问题,就是关于模型拟合程度的探讨与优化。根据此前的讨论,模型如果能很好的捕捉总体规律,就能够有较好的未知数据的预测效果。但限制模型捕捉总体规律的原因主要有两点:
- 其一,样本数据本身没有很好地反映总体规律
如果样本数据本身无法很好的反应总体规律,那建模的过程就算捕捉到了规律可能也无法适用于未知数据。举个极端的例子,在进行反欺诈检测时,如果要基于并未出现过欺诈案例的历史数据来进行建模,那模型就将面临无规律可捕捉的窘境,当然,确切的说,是无可用规律可捕捉;或者,当扰动项过大时,噪声也将一定程度上掩盖真实规律。 - 其二,样本数据能反应总体规律,但模型没有很好地捕捉到数据规律
如果数据能反应总体规律而模型效果不佳,则核心原因就在模型本身了。此前介绍过,机器学习模型评估主要依据模型在测试集上的表现,如果测试集效果不好,则我们认为模型还有待提升,但导致模型在测试集上效果不好的原因其实也主要有两点,其一是模型没捕捉到训练集上数据的规律,其二则是模型过分捕捉训练集上的数据规律,导致模型捕获了大量训练集独有的、无法适用于总体的规律(局部规律),而测试集也是从总体中来,这些规律也不适用于测试集。前一种情况我们称模型为欠拟合,后一种情况我们称模型为过拟合。
总结:
- 模型欠拟合:训练误差和测试误差均较大。模型没捕捉到训练集上数据的规律
- 模型过拟合:训练集上误差较小,但测试集上误差较大。模型过分捕捉训练集上的数据规律,导致模型捕获了大量训练集独有的、无法适用于总体的规律(局部规律)。过拟合产生的根本原因,还是样本之间有“误差”,或者不同批次的数据规律不完全一致。
二、模型欠拟合问题
1、模型欠拟合
# 导入自定义包
form mycode import *
# 一、数据加载与处理
# 设置随机数种子
import torch
torch.manual_seed(420)
# 创建最高项为2的多项式回归数据集 y = 2*x1^2 - x2^2
features, labels = tensorGenReg(w=[2, -1], bias=False, deg=2)
# 绘制图像查看数据分布
plt.subplot(121)
plt.scatter(features[:, 0], labels) # 2*x1^2
plt.subplot(122)
plt.scatter(features[:, 1], labels) # - x2^2

# 二、数据重载
# 进行数据集切分与加载 bs=10 rate=0.7
train_loader, test_loader = split_loader(features, labels)
# 三、网络架构与参数设置
class LR_class(nn.Module): # 没有激活函数
def __init__(self, in_features=2, out_features=1): # 定义模型的点线结构
super(LR_class, self).__init__()
self.linear = nn.Linear(in_features, out_features)
def forward(self, x): # 定义模型的正向传播规则
out = self.linear(x)
return out
# 四、实际训练流程
# 实例化模型
LR = LR_class()
train_l = [] # 列表容器,存储训练误差
test_l = [] # 列表容器,存储测试误差
num_epochs = 20
# 执行循环
for epochs in range(num_epochs):
fit(net = LR,
criterion = nn.MSELoss(),
optimizer = optim.SGD(LR.parameters(), lr = 0.03),
batchdata = train_loader,
epochs = epochs)
train_l.append(mse_cal(train_loader, LR).detach().numpy())
test_l.append(mse_cal(test_loader, LR).detach().numpy())
# 五、可视化结果显示
# 绘制图像,查看MSE变化情况
plt.plot(list(range(num_epochs)), train_l, label='train_mse')
plt.plot(list(range(num_epochs)), test_l, label='test_mse')
plt.legend(loc = 1)
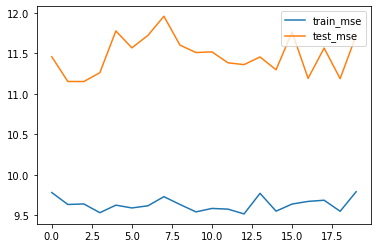
- 结果分析:
训练误差和测试误差均较大,模型存在欠拟合情况,考虑增加模型复杂程度。
2、提高模型复杂度
增加模型的线性层
# 三、网络架构与参数设置
class LR_class1(nn.Module):
def __init__(self, in_features=2, n_hidden=4, out_features=1):
super(LR_class1, self).__init__()
self.linear1 = nn.Linear(in_features, n_hidden)
self.linear2 = nn.Linear(n_hidden, out_features)
def forward(self, x):
z1 = self.linear1(x)
out = self.linear2(z1)
return out
# 四、实际训练流程
# 实例化模型
LR = LR_class()
train_l = [] # 列表容器,存储训练误差
test_l = [] # 列表容器,存储测试误差
num_epochs = 20
# 执行循环
for epochs in range(num_epochs):
fit(net = LR,
criterion = nn.MSELoss(),
optimizer = optim.SGD(LR.parameters(), lr = 0.03),
batchdata = train_loader,
epochs = epochs)
train_l.append(mse_cal(train_loader, LR).detach().numpy())
test_l.append(mse_cal(test_loader, LR).detach().numpy())
# 五、可视化结果显示
# 绘制图像,查看MSE变化情况
plt.plot(list(range(num_epochs)), train_l, label='train_mse')
plt.plot(list(range(num_epochs)), test_l, label='test_mse')
plt.legend(loc = 1)
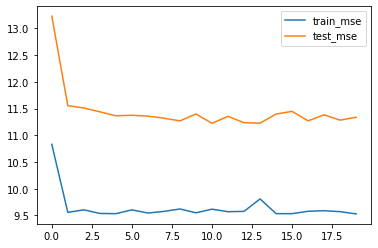
结果分析:结果没有显著提升,但模型稳定性却有所提升。对于叠加线性层的神经网络模型来说,由于模型只是对数据仿射变换,因此并不能满足拟合高次项的目的。也就是说,在增加模型复杂度的过程中,首先需要激活函数的配合,然后再是增加模型的层数和每层的神经元个数。
3、激活函数性能对比
# 三、网络架构与参数设置
# Sigmoid激活函数
class Sigmoid_class1(nn.Module):
def __init__(self, in_features=2, n_hidden=4, out_features=1, bias = True):
super(Sigmoid_class1, self).__init__()
self.linear1 = nn.Linear(in_features, n_hidden, bias=bias)
self.linear2 = nn.Linear(n_hidden, out_features, bias=bias)
def forward(self, x):
z1 = self.linear1(x)
p1 = torch.sigmoid(z1) # sigmoid
out = self.linear2(p1)
return out
# tanh激活函数
class tanh_class1(nn.Module):
def __init__(self, in_features=2, n_hidden=4, out_features=1, bias = True):
super(tanh_class1, self).__init__()
self.linear1 = nn.Linear(in_features, n_hidden, bias=bias)
self.linear2 = nn.Linear(n_hidden, out_features, bias=bias)
def forward(self, x):
z1 = self.linear1(x)
p1 = torch.tanh(z1) # tanh
out = self.linear2(p1)
return out
# ReLU激活函数
class ReLU_class1(nn.Module):
def __init__(self, in_features=2, n_hidden=4, out_features=1, bias = True):
super(ReLU_class1, self).__init__()
self.linear1 = nn.Linear(in_features, n_hidden, bias=bias)
self.linear2 = nn.Linear(n_hidden, out_features, bias=bias)
def forward(self, x):
z1 = self.linear1(x)
p1 = torch.relu(z1) # relu
out = self.linear2(p1)
return out
# 四、实际训练流程
# 实例化模型
LR = LR_class()
LR1 = LR_class1()
sigmoid_model1 = Sigmoid_class1()
tanh_model1 = tanh_class1()
relu_model1 = ReLU_class1()
model_l = [LR1, sigmoid_model1, tanh_model1, relu_model1] # 将实例化后模型放在一个列表容器中
name_l = ['LR1', 'sigmoid_model1', 'tanh_model1', 'relu_model1']
# 参数定义
num_epochs = 30
lr = 0.03
# 记录损失函数结果
mse_train = torch.zeros(len(model_l), num_epochs)
mse_test = torch.zeros(len(model_l), num_epochs)
# 训练模型
for epochs in range(num_epochs):
for i, model in enumerate(model_l):
fit(net = model,
criterion = nn.MSELoss(),
optimizer = optim.SGD(model.parameters(), lr = lr),
batchdata = train_loader,
epochs = epochs)
mse_train[i][epochs] = mse_cal(train_loader, model).detach()
mse_test[i][epochs] = mse_cal(test_loader, model).detach()
# 五、可视化结果显示
# 训练误差
for i, name in enumerate(name_l):
plt.plot(list(range(num_epochs)), mse_train[i], label=name)
plt.legend(loc = 1)
plt.title('mse_train')
# 测试误差
for i, name in enumerate(name_l):
plt.plot(list(range(num_epochs)), mse_test[i], label=name)
plt.legend(loc = 1)
plt.title('mse_test')
# 训练误差和测试误差
for i, name in enumerate(name_l):
plt.plot(list(range(num_epochs)), mse_test[i], label=name+'_train')
plt.plot(list(range(num_epochs)), mse_train[i], label=name+'_test')
plt.legend(loc = 1)
plt.title('mse_train_test')
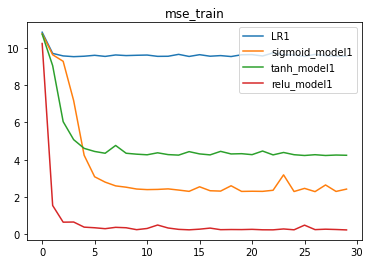
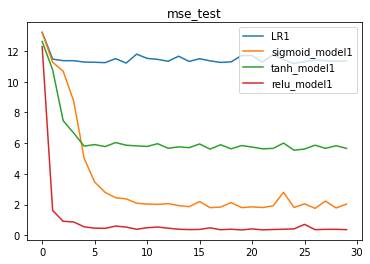
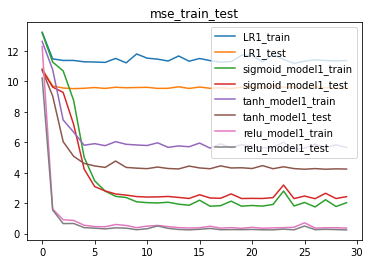
结果分析:从当前的实验能够看出,相比其他激活函数,ReLU激活函数效果明显更好。
效果:relu > sigmoid > tanh > linear
4、探索模型复杂度与激活函数
4.1 增加隐藏层的层数和激活函数relu
# 三、网络架构与参数设置
class ReLU_class2(nn.Module):
def __init__(self, in_features=2, n_hidden_1=4, n_hidden_2=4, out_features=1, bias=True):
super(ReLU_class2, self).__init__()
self.linear1 = nn.Linear(in_features, n_hidden_1, bias=bias)
self.linear2 = nn.Linear(n_hidden_1, n_hidden_2, bias=bias)
self.linear3 = nn.Linear(n_hidden_2, out_features, bias=bias)
def forward(self, x):
z1 = self.linear1(x)
p1 = torch.relu(z1)
z2 = self.linear2(p1)
p2 = torch.relu(z2)
out = self.linear3(p2)
return out
# 四、实际训练流程
# 实例化模型
relu_model1 = ReLU_class1()
relu_model2 = ReLU_class2()
# 模型列表容器
model_l = [relu_model1, relu_model2]
name_l = ['relu_model1', 'relu_model2']
# 核心参数
num_epochs = 20
lr = 0.03
# 记录损失函数结果
mse_train = torch.zeros(len(model_l), num_epochs)
mse_test = torch.zeros(len(model_l), num_epochs)
# 训练模型
for epochs in range(num_epochs):
for i, model in enumerate(model_l):
fit(net = model,
criterion = nn.MSELoss(),
optimizer = optim.SGD(model.parameters(), lr = lr),
batchdata = train_loader,
epochs = epochs)
mse_train[i][epochs] = mse_cal(train_loader, model).detach()
mse_test[i][epochs] = mse_cal(test_loader, model).detach()
# 五、可视化结果显示
# 训练误差
for i, name in enumerate(name_l):
plt.plot(list(range(num_epochs)), mse_train[i], label=name)
plt.legend(loc = 1)
plt.title('mse_train')
# 测试误差
for i, name in enumerate(name_l):
plt.plot(list(range(num_epochs)), mse_test[i], label=name)
plt.legend(loc = 1)
plt.title('mse_test')
# 训练误差和测试误差
for i, name in enumerate(name_l):
plt.plot(list(range(num_epochs)), mse_test[i], label=name+'_train')
plt.plot(list(range(num_epochs)), mse_train[i], label=name+'_test')
plt.legend(loc = 1)
plt.title('mse_train_test')
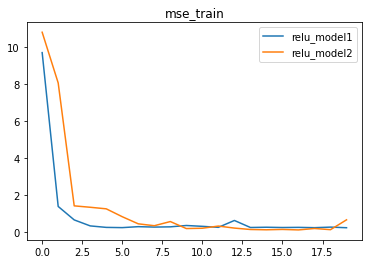
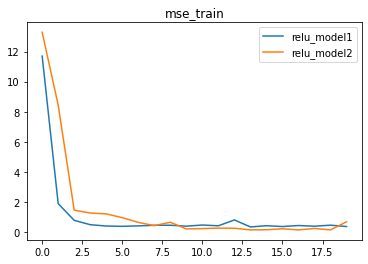
我们发现,模型效果并没有明显提升,反而出现了更多的波动,迭代收敛速度也有所下降。模型效果无法提升是不是因为模型还不够复杂,如果继续尝试添加隐藏层会有什么效果?
4.2 ReLU激活函数在堆叠过程中的表现
# 三、网络架构与参数设置
# 构建三个隐藏层的神经网络
class ReLU_class3(nn.Module):
def __init__(self, in_features=2, n_hidden1=4, n_hidden2=4, n_hidden3=4, out_features=1, bias=True):
super(ReLU_class3, self).__init__()
self.linear1 = nn.Linear(in_features, n_hidden1, bias=bias)
self.linear2 = nn.Linear(n_hidden1, n_hidden2, bias=bias)
self.linear3 = nn.Linear(n_hidden2, n_hidden3, bias=bias)
self.linear4 = nn.Linear(n_hidden3, out_features, bias=bias)
def forward(self, x):
z1 = self.linear1(x)
p1 = torch.relu(z1)
z2 = self.linear2(p1)
p2 = torch.relu(z2)
z3 = self.linear3(p2)
p3 = torch.relu(z3)
out = self.linear4(p3)
return out
# 构建四个隐藏层的神经网络
class ReLU_class4(nn.Module):
def __init__(self, in_features=2, n_hidden1=4, n_hidden2=4, n_hidden3=4, n_hidden4=4, out_features=1, bias=True):
super(ReLU_class4, self).__init__()
self.linear1 = nn.Linear(in_features, n_hidden1, bias=bias)
self.linear2 = nn.Linear(n_hidden1, n_hidden2, bias=bias)
self.linear3 = nn.Linear(n_hidden2, n_hidden3, bias=bias)
self.linear4 = nn.Linear(n_hidden3, n_hidden4, bias=bias)
self.linear5 = nn.Linear(n_hidden4, out_features, bias=bias)
def forward(self, x):
z1 = self.linear1(x)
p1 = torch.relu(z1)
z2 = self.linear2(p1)
p2 = torch.relu(z2)
z3 = self.linear3(p2)
p3 = torch.relu(z3)
z4 = self.linear4(p3)
p4 = torch.relu(z4)
out = self.linear5(p4)
return out
# 四、实际训练流程
# 实例化模型
relu_model1 = ReLU_class1()
relu_model2 = ReLU_class2()
relu_model3 = ReLU_class3()
relu_model4 = ReLU_class4()
# 模型列表容器
model_l = [relu_model1, relu_model2, relu_model3, relu_model4]
name_l = ['relu_model1', 'relu_model2', 'relu_model3', 'relu_model4']
# 核心参数
num_epochs = 20
lr = 0.03
# 记录损失函数结果
mse_train = torch.zeros(len(model_l), num_epochs)
mse_test = torch.zeros(len(model_l), num_epochs)
# 训练模型
for epochs in range(num_epochs):
for i, model in enumerate(model_l):
fit(net = model,
criterion = nn.MSELoss(),
optimizer = optim.SGD(model.parameters(), lr = lr),
batchdata = train_loader,
epochs = epochs)
mse_train[i][epochs] = mse_cal(train_loader, model).detach()
mse_test[i][epochs] = mse_cal(test_loader, model).detach()
# 五、可视化结果显示
# 训练误差
for i, name in enumerate(name_l):
plt.plot(list(range(num_epochs)), mse_train[i], label=name)
plt.legend(loc = 1)
plt.title('mse_train')
# 测试误差
for i, name in enumerate(name_l):
plt.plot(list(range(num_epochs)), mse_test[i], label=name)
plt.legend(loc = 1)
plt.title('mse_test')
# 训练误差和测试误差
for i, name in enumerate(name_l):
plt.plot(list(range(num_epochs)), mse_test[i], label=name+'_train')
plt.plot(list(range(num_epochs)), mse_train[i], label=name+'_test')
plt.legend(loc = 1)
plt.title('mse_train_test')
relu结果
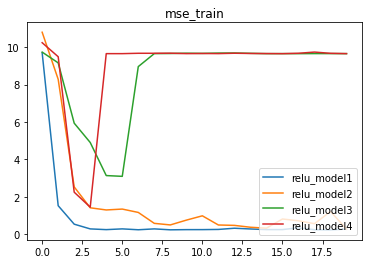

我们发现,在堆叠ReLU激活函数的过程中,模型效果并没有朝向预想的方向发展,MSE不仅没有越来越低,model3和model4甚至出现了模型失效的情况!
这充分的说明,在当前技术手段下,模型构建并非越复杂越好。同时我们能够清晰的看到,伴随模型复杂度增加,模型收敛速度变慢、收敛过程波动增加、甚至有可能出现模型失效的情况。
但同时我们又知道,深度学习本身就是一种构建复杂模型的方法,并且其核心价值就在于使用深度神经网络处理海量数据。从根本上来说,当前实验复杂模型出现问题并不是算法理论本身出了问题,而是我们缺乏了解决这些问题的“技术手段”,只有掌握了这些“技术手段”之后,才能真正构建运行高效、泛化能力强的模型。而这些技术手段,就是模型优化方法。其实这也从侧面说明了优化算法的重要性。
4.3 Sigmoid激活函数在堆叠过程中的表现
# 三、网络架构与参数设置
class Sigmoid_class2(nn.Module):
def __init__(self, in_features=2, n_hidden1=4, n_hidden2=4, out_features=1):
super(Sigmoid_class2, self).__init__()
self.linear1 = nn.Linear(in_features, n_hidden1)
self.linear2 = nn.Linear(n_hidden1, n_hidden2)
self.linear3 = nn.Linear(n_hidden2, out_features)
def forward(self, x):
z1 = self.linear1(x)
p1 = torch.sigmoid(z1)
z2 = self.linear2(p1)
p2 = torch.sigmoid(z2)
out = self.linear3(p2)
return out
class Sigmoid_class3(nn.Module):
def __init__(self, in_features=2, n_hidden1=4, n_hidden2=4, n_hidden3=4, out_features=1):
super(Sigmoid_class3, self).__init__()
self.linear1 = nn.Linear(in_features, n_hidden1)
self.linear2 = nn.Linear(n_hidden1, n_hidden2)
self.linear3 = nn.Linear(n_hidden2, n_hidden3)
self.linear4 = nn.Linear(n_hidden3, out_features)
def forward(self, x):
z1 = self.linear1(x)
p1 = torch.sigmoid(z1)
z2 = self.linear2(p1)
p2 = torch.sigmoid(z2)
z3 = self.linear3(p2)
p3 = torch.sigmoid(z3)
out = self.linear4(p3)
return out
class Sigmoid_class4(nn.Module):
def __init__(self, in_features=2, n_hidden1=4, n_hidden2=4, n_hidden3=4, n_hidden4=4, out_features=1):
super(Sigmoid_class4, self).__init__()
self.linear1 = nn.Linear(in_features, n_hidden1)
self.linear2 = nn.Linear(n_hidden1, n_hidden2)
self.linear3 = nn.Linear(n_hidden2, n_hidden3)
self.linear4 = nn.Linear(n_hidden3, n_hidden4)
self.linear5 = nn.Linear(n_hidden4, out_features)
def forward(self, x):
z1 = self.linear1(x)
p1 = torch.sigmoid(z1)
z2 = self.linear2(p1)
p2 = torch.sigmoid(z2)
z3 = self.linear3(p2)
p3 = torch.sigmoid(z3)
z4 = self.linear4(p3)
p4 = torch.sigmoid(z4)
out = self.linear5(p4)
return out
# 四、实际训练流程
# 实例化模型
sigmoid_model1 = Sigmoid_class1()
sigmoid_model2 = Sigmoid_class2()
sigmoid_model3 = Sigmoid_class3()
sigmoid_model4 = Sigmoid_class4()
# 模型列表容器
model_l = [sigmoid_model1, sigmoid_model2, sigmoid_model3, sigmoid_model4]
name_l = ['sigmoid_model1', 'sigmoid_model2', 'sigmoid_model3', 'sigmoid_model4']
# 核心参数
num_epochs = 50
lr = 0.03
# 记录损失函数结果
mse_train = torch.zeros(len(model_l), num_epochs)
mse_test = torch.zeros(len(model_l), num_epochs)
# 训练模型
for epochs in range(num_epochs):
for i, model in enumerate(model_l):
fit(net = model,
criterion = nn.MSELoss(),
optimizer = optim.SGD(model.parameters(), lr = lr),
batchdata = train_loader,
epochs = epochs)
mse_train[i][epochs] = mse_cal(train_loader, model).detach()
mse_test[i][epochs] = mse_cal(test_loader, model).detach()
# 五、可视化结果显示
# 训练误差
for i, name in enumerate(name_l):
plt.plot(list(range(num_epochs)), mse_train[i], label=name)
plt.legend(loc = 1)
plt.title('mse_train')
# 测试误差
for i, name in enumerate(name_l):
plt.plot(list(range(num_epochs)), mse_test[i], label=name)
plt.legend(loc = 1)
plt.title('mse_test')
# 训练误差和测试误差
for i, name in enumerate(name_l):
plt.plot(list(range(num_epochs)), mse_test[i], label=name+'_train')
plt.plot(list(range(num_epochs)), mse_train[i], label=name+'_test')
plt.legend(loc = 1)
plt.title('mse_train_test')
sigmoid结果
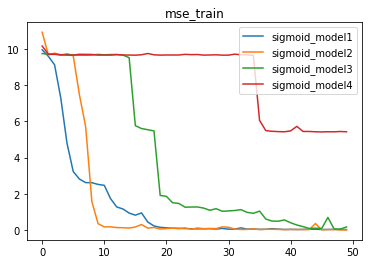
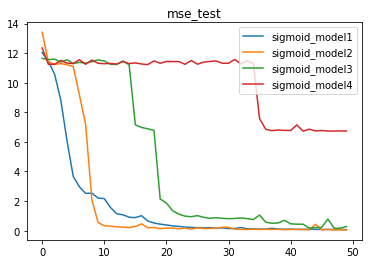
sigmoid激活函数的简单叠加也出现了很多问题,虽然没有像ReLU叠加一样出现大幅MSE升高的情况,但仔细观察,不难发现,对于model1、model2、model3来说,伴随模型复杂增加,模型效果没有提升,但收敛速度却下降的很严重,而model4更是没有收敛到其他几个模型的MSE,问题不小。不过相比ReLU激活函数,整体收敛过程确实稍显稳定,而Sigmoid也是老牌激活函数,在2000年以前,是最主流的激活函数。
此处Sigmoid激活函数堆叠后出现的问题,本质上就是梯度消失所导致的问题。
4.4 tanh激活函数在堆叠过程中的表现
# 三、网络架构与参数设置
class tanh_class2(nn.Module):
def __init__(self, in_features=2, n_hidden1=4, n_hidden2=4, out_features=1):
super(tanh_class2, self).__init__()
self.linear1 = nn.Linear(in_features, n_hidden1)
self.linear2 = nn.Linear(n_hidden1, n_hidden2)
self.linear3 = nn.Linear(n_hidden2, out_features)
def forward(self, x):
z1 = self.linear1(x)
p1 = torch.tanh(z1)
z2 = self.linear2(p1)
p2 = torch.tanh(z2)
out = self.linear3(p2)
return out
class tanh_class3(nn.Module):
def __init__(self, in_features=2, n_hidden1=4, n_hidden2=4, n_hidden3=4, out_features=1):
super(tanh_class3, self).__init__()
self.linear1 = nn.Linear(in_features, n_hidden1)
self.linear2 = nn.Linear(n_hidden1, n_hidden2)
self.linear3 = nn.Linear(n_hidden2, n_hidden3)
self.linear4 = nn.Linear(n_hidden3, out_features)
def forward(self, x):
z1 = self.linear1(x)
p1 = torch.tanh(z1)
z2 = self.linear2(p1)
p2 = torch.tanh(z2)
z3 = self.linear3(p2)
p3 = torch.tanh(z3)
out = self.linear4(p3)
return out
class tanh_class4(nn.Module):
def __init__(self, in_features=2, n_hidden1=4, n_hidden2=4, n_hidden3=4, n_hidden4=4, out_features=1):
super(tanh_class4, self).__init__()
self.linear1 = nn.Linear(in_features, n_hidden1)
self.linear2 = nn.Linear(n_hidden1, n_hidden2)
self.linear3 = nn.Linear(n_hidden2, n_hidden3)
self.linear4 = nn.Linear(n_hidden3, n_hidden4)
self.linear5 = nn.Linear(n_hidden4, out_features)
def forward(self, x):
z1 = self.linear1(x)
p1 = torch.tanh(z1)
z2 = self.linear2(p1)
p2 = torch.tanh(z2)
z3 = self.linear3(p2)
p3 = torch.tanh(z3)
z4 = self.linear4(p3)
p4 = torch.tanh(z4)
out = self.linear5(p4)
return out
# 四、实际训练流程
# 实例化模型
tanh_model1 = tanh_class1()
tanh_model2 = tanh_class2()
tanh_model3 = tanh_class3()
tanh_model4 = tanh_class4()
# 模型列表容器
model_l = [tanh_model1, tanh_model2, tanh_model3, tanh_model4]
name_l = ['tanh_model1', 'tanh_model2', 'tanh_model3', 'tanh_model4']
# 核心参数
num_epochs = 50
lr = 0.03
# 记录损失函数结果
mse_train = torch.zeros(len(model_l), num_epochs)
mse_test = torch.zeros(len(model_l), num_epochs)
# 训练模型
for epochs in range(num_epochs):
for i, model in enumerate(model_l):
fit(net = model,
criterion = nn.MSELoss(),
optimizer = optim.SGD(model.parameters(), lr = lr),
batchdata = train_loader,
epochs = epochs)
mse_train[i][epochs] = mse_cal(train_loader, model).detach()
mse_test[i][epochs] = mse_cal(test_loader, model).detach()
# 五、可视化结果显示
# 训练误差
for i, name in enumerate(name_l):
plt.plot(list(range(num_epochs)), mse_train[i], label=name)
plt.legend(loc = 1)
plt.title('mse_train')
# 测试误差
for i, name in enumerate(name_l):
plt.plot(list(range(num_epochs)), mse_test[i], label=name)
plt.legend(loc = 1)
plt.title('mse_test')
# 训练误差和测试误差
for i, name in enumerate(name_l):
plt.plot(list(range(num_epochs)), mse_test[i], label=name+'_train')
plt.plot(list(range(num_epochs)), mse_train[i], label=name+'_test')
plt.legend(loc = 1)
plt.title('mse_train_test')
tanh结果

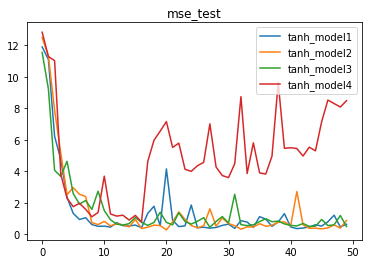
tanh激活函数叠加效果中规中矩,在model1到model2的过程效果明显向好,MSE基本一致、收敛速度基本一致、但收敛过程稳定性较好,也证明模型结果较为可信,而model3、model4则表现出了和前面两种激活函数在叠加过程中所出现的类似的问题,当然对于tanh来说,最明显的问题是出现了剧烈波动,甚至出现了“跳跃点”。
此处tanh激活函数堆叠所导致的迭代过程剧烈波动的问题,也被称为迭代不平稳,需要优化迭代过程来解决。
5、模型复杂度和不同激活函数的讨论
- 模型复杂度的讨论
我们发现,在堆叠ReLU激活函数的过程中,模型效果并没有朝向预想的方向发展,MSE不仅没有越来越低,model3和model4甚至出现了模型失效的情况!
这充分的说明,在当前技术手段下,模型构建并非越复杂越好。同时我们能够清晰的看到,伴随模型复杂度增加,模型收敛速度变慢、收敛过程波动增加、甚至有可能出现模型失效的情况。
但同时我们又知道,深度学习本身就是一种构建复杂模型的方法,并且其核心价值就在于使用深度神经网络处理海量数据。从根本上来说,当前实验复杂模型出现问题并不是算法理论本身出了问题,而是我们缺乏了解决这些问题的“技术手段”,只有掌握了这些“技术手段”之后,才能真正构建运行高效、泛化能力强的模型。而这些技术手段,就是模型优化方法。其实这也从侧面说明了优化算法的重要性。
- 不同激活函数存在的问题
不同激活函数在深层次神经网络运行时存在的不同问题
- ReLU激活函数叠加后出现的模型失效问题,也就是Dead ReLU Problem。
- Sigmoid激活函数堆叠后出现的问题,本质上就是梯度消失所导致的问题。
- tanh激活函数堆叠所导致的迭代过程剧烈波动的问题,也被称为迭代不平稳,需要优化迭代过程来解决。
三、神经网络结构选择策略
1、层数选择
- 三层以内:模型效果会随着层数增加而增加;
- 三层至六层:随着层数的增加,模型迭代的稳定性会受到影响,并且这种影响是随着层数增加“指数级”增加的,此时我们就需要采用一些优化方法对输入数据、激活函数、损失函数和迭代过程进行优化,一般来说在六层以内的神经网络在通用的优化算法配合下,是能够收敛至一个较好的结果的;
- 六层以上:在模型超过六层之后,优化方法在一定程度上仍然能够辅助模型训练,但此时保障模型正常训练的更为核心的影响因素,就变成了数据量本身和算力。
- 神经网络模型要迭代收敛至一个稳定的结果,所需的epoch是随着神经网络层数增加而增加的,也就是说神经网络模型越复杂,收敛所需迭代的轮数就越多,此时所需的算力也就越多。而另一方面,伴随着模型复杂度增加,训练所需的数据量也会增加,如果是复杂模型应用于小量样本数据,则极有可能会出现“过拟合”的问题从而影响模型的泛化能力。当然,伴随着模型复杂度提升、所需训练数据增加,对模型优化所采用的优化算法也会更加复杂。也就是说,六层以内神经网络应对六层以上的神经网络模型,我们需要更多的算力支持、更多的数据量、以及更加复杂的优化手段支持。
2、神经元的个数
- 输入层的神经元个数就是特征个数
- 输出层神经元个数,如果是回归类问题或者是逻辑回归解决二分类问题,输出层就只有一个神经元,而如果是多分类问题,输出层神经元个数就是类别总数。
- 隐藏层神经元个数,可以按照最多不超过输入特征的2-4倍进行设置,当然默认连接方式是全连接,每一个隐藏层可以设置相同数量的神经元。其实对于神经元个数设置来说,后期是有调整空间的,哪怕模型创建过程神经元数量有些“饱和”,我们后期我们可以通过丢弃法(优化方法的一种)对隐藏层神经元个数和连接方式进行修改。对于某些非结构化数据来说,隐藏层神经元个数也会根据数据情况来进行设置,如神经元数量和图像关键点数量匹配等。
3、激活函数使用的单一性
同时,对于激活函数的交叉使用,我们需要知道,通常来说,是不会出现多种激活函数应用于一个神经网络中的情况的。主要原因并不是因为模型效果就一定会变差,而是如果几种激活函数效果类似,那么交叉使用几种激活函数其实效果和使用一种激活函数区别不大,而如果几种激活函数效果差异非常明显,那么这几种激活函数的堆加就会使得模型变得非常不可控。此前的实验让我们深刻体会优化算法的必要性,但目前工业界所掌握的、针对激活函数的优化算法都是针对某一种激活函数来使用的,激活函数的交叉使用会令这些优化算法失效。因此,尽管机器学习模型是“效果为王”,但在基础理论没有进一步突破之前,不推荐在一个神经网路中使用多种激活函数。