paper:Re-parameterizing Your Optimizers rather than Architectures
offcial implementation:https://github.com/dingxiaoh/repoptimizers
背景
神经网络的结构设计是将先验知识融入模型中。例如将特征转换建模成残差相加的形式(\(y=f(x)+x\))效果优于普通形式(\(y=f(x)\)),ResNet通过shortcut结构将这种先验知识融入到模型中。作者发现,尽管我们不断地将对模型的最新理解融入到模型结构设计中,但训练时采用的都是通用的优化器比如SGD和AdamW等,即没有将先验知识融入到optimizer中,这些优化器都是model-agnostic的。
本文的创新点
本文提出了一种称为“梯度重参数化”(Gradient Re-parameterization)的新方法,该方法根据模型特定的超参数修改梯度,从而创建出一种新的重参数优化器(RepOptimizer),从而可以直接在优化过程中利用模型特定的先验知识,而不仅仅依赖于架构设计。
本文的主要创新如下
1. 梯度重参数化(SR)
- 这种方法根据模型特定的超参数修改梯度,在优化过程中整合模型特定的先验知识,然后再更新模型参数。
- 与传统的优化器不同,GR不会在训练过程中引入额外的参数或统计量,而是根据从模型结构中得到的超参数调整训练动态。
2. 重参数化优化器(RepOptimizer)
- 利用GR整合结构先验知识到优化过程中。
- 通过一个VGG风格的模型RepOpt-VGG来展示,简单模型使用RepOptimizer训练后,可以达到或超过那些设计精良的复杂模型的性能。
3. 与结构重参数化的比较
- 重参数优化器在训练过程中不需要额外的前向/后向计算或内存开销,而诸如RepVGG的方法在训练时需要添加额外的结构并在训练后进行转换。
- 这种效率对于提高训练和推理速度特别有利,使RepOpt-VGG在计算资源有限或需要快速模型迭代的应用场景中成为实际选择。
4. 量化优化性
- RepOpt-VGG克服了量化问题。在使用简单的INT8后训练量化(PTQ)时,RepVGG在ImageNet上的准确率显著下降,而RepOpt-VGG没有经过结构转换,因此更加友好量化。
方法介绍
RepOptimizer的核心是我们想要利用的先验知识。在RepOpt-VGG中,这种先验知识是:模型的性能可以通过将按不同权重加权的多个分支的输入和输出相加来提高。这种简单的知识带来了多种结构设计,比如ResNet简单地将residual block的输入输出相加。RepVGG也有相同的想法,但使用了不同的实现。本文选择了RepVGG的结构设计(3x3 conv + 1x1 conv + identity mapping)来进行改进。
接下来就是如何将结构先验融入到RepOptimizer中。作者注意到关于上述先验知识的一个有趣现象:在一种特殊情况下,当每个分支只包含一个线性可训练的算子和一个可选的常量缩放系数,如果缩放系数的值设置的合理,模型的性能仍然会提高。作者将这种linear block称为Constant-Scale Linear Addition(CSLA)。作者发现我们可以通过将梯度乘以一些由constant scales得到的常数乘数,用单个算子替换一个CSLA block并实现相同的训练dynamics(即在给定相同的训练数据后,它们经过任意数量的训练迭代后,总是产生相同的输出)。我们将这种乘数称为Grad Mult。梯度与Grad Mult相乘可以看作GR的一个具体实现。

接下来我们给出CSLA=GR的证明过程。
CSLA表示每个分支只包含一个具有可训练参数的线性可微算子(例如conv、FC、scaling layer)且不包含训练时的非线性比如BN或dropout。用SGD训练一个CSLA等价于用修改后的梯度训练一个单独的算子。
我们从一个简单的情况开始,其中CSLA block有两个分支,每个分支是一个kernel大小相同的卷积和一个常量缩放系数。我们用 \(\alpha_A,\alpha_B\) 表示这两个常量,\(W^{(A)},W^{(B)}\) 表示两个卷积核,\(X,Y\) 分别表示输入和输出。则CSLA的计算过程可以表示为 \(Y_{CSLA}=\alpha_A(X*W^{(A)})+\alpha_B(X*W^{(B)})\),其中 \(*\) 表示卷积。对于GR,我们直接训练参数为 \(W'\) 的目标结构,则 \(Y_{GR}=X*W'\)。假设目标函数是 \(L\),训练迭代次数为 \(i\),一个特定卷积核 \(W\) 的梯度为 \(\frac{\partial L}{\partial W} \),\(F(\frac{\partial L}{\partial W'} )\) 表示GR对应梯度的任意变换。
因此需要证明的是存在一个只由 \(\alpha_A,\alpha_B\) 决定的变换 \(F\),使得用 \(F(\frac{\partial L}{\partial W'} )\) 更新 \(W'\) 可以确保下式成立

根据卷积的叠加性和齐次性等价于确保下式成立

在第0个iteration,正确的初始化可以确保等式成立。假设 \(W^{(A)(0)},W^{(B)(0)}\) 是任意初始化的值,初始条件是

从而有

接下来我们用数学归纳法来证明,对 \(W'\) 的梯度进行适当的变换,等式恒成立。设学习率为 \(\lambda\),权重按下式更新

在更新了CSLA block后我们有

我们使用 \(F(\frac{\partial L}{\partial W'} )\) 来更新 \(W'\)
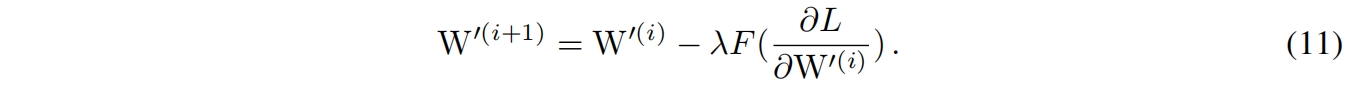
假设等式在iteration \(i(i\ge0)\) 成立,根据式(6)(10)(11),我们必须确保

对式(6)求偏导,我们有

最终我们就有了

在式(8)初始条件成立下,当 \(\alpha_AW^{(A)(i)}+\alpha_BW^{(B)(i)}=W'(i)\),根据式(14)我们有 \(\alpha_AW^{(A)(i+1)}+\alpha_BW^{(B)(i+1)}=W'(i+1)\),根据数学归纳法,任意 \(i\ge0\) 都成立。至此证明完成。
总结一下,我们用于更新对应GR的算子的梯度应该被简单地用一个常数因子进行缩放,即 \((\alpha^2_{A}+\alpha^2_B)\)。根据我们的定义,这正是我们想要构造具有恒定尺度的Grad Mult的公式。
在实际训练中,\(i\) 表示训练iteration,只要遵循下面两条规则,我们就能确保 \(\mathrm{Y}_{C S L A}^{(i)}=\mathrm{Y}_{G R}^{(i)}, \forall i \geq 0\)
Rule of Initialization:\(W'\) 应该初始化为 \(\mathrm{W}^{\prime(0)} \leftarrow \alpha_A \mathrm{~W}^{(A)(0)}+\alpha_B \mathrm{~W}^{(B)(0)}\)。
Rule of Iteration:当CSLA用普通的SGD(momentum是可选的)进行更新时,对应的GR的梯度应该乘以 \((\alpha^2_{A}+\alpha^2_B)\)。即下式

有了CSLA=GR,我们首先通过设计CSLA的结构来设计和描述RepOptimizer的行为。。对于RepOpt-VGG,我们用一个常量的channel-wise缩放来替代原本RepVGG block中3x3和1x1卷积后的BN,并用一个可训练的channel-wise缩放替代identity分支中的BN,以此来实例化CSLA。我们这样做的原因是CSLA的每个分支中不能有超过一个线性可训练的算子。
当不同分支卷积核的大小不一样时,Grad Mult是一个张量,应该用对应位置的scale来计算梯度。以对应这样的一个CSLA block用Grad Mult训练单个3x3卷积为例 ,\(C\) 是通道数,\(\mathbf{s}, \mathbf{t} \in \mathbb{R}^C\) 分别是3x3和1x1卷积层后的常量channel-wise缩放尺度,则Grad Mult矩阵 \(M^{C\times C\times 3\times 3}\) 按下式构建

其中 \(p=2\) 和 \(q=2\) 意味着3x3卷积核的中心和1x1分支有关(就像RepVGG block将1x1卷积融合到3x3卷积的中心点一样)。由于可训练的channel-wise scaling可以看作一个1x1深度卷积后跟一个常量缩放因子1,我们将Grad Mult对角线位置的值设为1。
与RepVGG等常见的SR形式相比,CSLA block训练阶段没有像BN这样的非线性算子也没有连续的可训练算子,并且也可以通过常用的SR技术转换为等价的结构从而得到相同的推理结果。但是推理时的等价并不意味着训练时的等价,因为转换后的结构会有不同的training dynamics,在更新后打破等价性。此外,必须强调的是CSLA结构是假想的,它只是用于描述和可视化RepOptimizer的中间工具,但我们实际上并没有训练它,因为直接用GR训练目标结构得到的结果在数学上时相等的。
Hyper-Search
关于常量 \(\mathbf{s}\) 和 \(\mathbf{t}\),作者提出了一种新的方法将优化器的超参和一个辅助模型的可训练参数联系起来,称为Hyper-Search(HS)。给定一个RepOptimizer,我们将其对应的CSLA模型中的常量scales用可训练的scales代替来构建一个辅助的Hyper-Search模型并在一个小的搜索数据集上训练(比如CIFAR-100)。HS受到了DARTS的启发,即可训练参数的最终值是模型期望它们成为的值,所以可训练scale的最终值就是在想象的CSLA模型中我们希望得到的常量值。通过CSLA=GR,CSLA模型中的期望常数正是我们构建RepOptimizer的所需要的Grad Mult。
Train with RepOptimizer
在HS后,我们用搜索得到的常量 \(\mathbf{s}\) 和 \(\mathbf{t}\) 来构建Grad Mult并保存在内存中。在目标数据集上训练目标模型时,在每个iteration后RepOptimizer将Grad Mult与对应算子的梯度相乘。
实验结果
在HS过程中,trainable scales根据网络层的深度进行初始化,具体初始化为 \(\sqrt{\frac{2}{l}}\),背后的直觉是让更深的网络层在初始化时表现的更像identity mapping来促进训练。
为了公平比较,RepOpt-VGG采用了和RepVGG相同的简单架构,除了第一个stride=2的3x3 conv,我们将多个3x3 conv分成四个stage,每个stage的第一层stride=2,最后再添加一个global average pooling层和一个FC层。每个stage的层数和通道数如表1所示

RepOpt-VGG和RepVGG的结果对比如表2所示,可以得到以下观察结果:1)RepOpt-VGG占用的内存更少,训练速度更快。在使用各自最大的batch size时RepOpt-VGG-B1比RepVGG-B1快了1.8x。2)随着batch size的增大,每个模型的性能都会提高,这可能是因为BN的稳定性更高。这也强调了RepOptimizer的内存效率更高可以允许更大的batch size。3)RepOpt-VGG的准确性与RepVGG非常match,表明在训练效率和准确性之间有明显更好的平衡。

HS阶段是在CIFAR-100数据集上训练的,然后迁移到ImageNet,这表明RepOptimizer可能是model-specific但是dataset-agnostic。作者进一步研究了在ImageNet和Caltech256数据集上进行hyper-search并用Caltech256作为另一个目标数据集,结果如下

从表5我们可以得到如下观察:1)在目标数据集上搜索到的RepOptimizer超参并不比在不同数据集上搜索到的超参的效果更好。通过在ImageNet上进行搜索和训练,最终的准确率为78.43%,与CIFAR搜索到的RepOptimizer的结果非常吻合。需要注意的事,在ImageNet上搜索并不意味着在ImageNet上训练相同的模型两次,因为第二次训练只继承了HS模型训练得到的scales到RepOptimizer中,而不是其他训练参数。2)对于不同的超参数源,RepOptimizer在目标数据集上的结果相似,这表明RepOptimizer是与数据集无关的。
有趣的是,搜索数据集上的精度并不能反映目标数据集上的精度。由于RepOpt-VGG是针对ImageNet设计的,它有5个stride=2的降采样层,在CIFAR-100上训练其对应的HS模型似乎是不合理的,因为CIFAR-100数据集的图片分辨率为32x32,这意味和最后两个stage中的卷积是在2x2和1x1的feature map上进行的。如表6所示,和预期的一样,HS模型在CIFAR-100上的精度只有54.53%,但搜索到的RepOptimizer在ImageNet上的效果很好。当我们降低CIFAR-100上HS模型的降采样率,HS模型的精度有所提高,但目标模型上对应的RepOpt-VGG模型的精度也降低了。这作为另外一个证据也表明了搜索到的常量是针对模型的model-specific,因此RepOptimizer也是model-specific的。原始模型的降采样ratio为32x,但修改stride后使一个不同的HS模型的降采样率为16x,在这个HS模型上搜索得到的常量在原始降采样率为32x模型上的效果并不好。

最后,作者还比较了RepOpt-VGG和RepVGG量化的效果,如表8所示。可以看到对结构重参数化模型进行量化后精度下降严重只有54.55%,而RepOpt-VGG量化后精度只下降了2.5%。作者表明结构转换(BN融合和分支相加)导致了不利于量化的参数分布,而RepOptimizer则没有这个问题,因为它本身就没有结构上的转换。

代码解析
1. 当mode为hs或csla时,block为LinearAddBlock,当csla时LinearAddBlock中的两个scale为常量。即hs时两个scale是可训练的,当hs结束后训练target网络时直接用搜索得到的两个scale,此时两个scale是常量。
2. LinearAddBlock是2个或3个分支,3x3 conv + scale,1x1 conv + scale,当输入和输出通道相等且stride=1时,第3个identity分支是一个scale。
3. 当mode='target'时,即训练目标网络,block为RealVGGBlock,其中包括3x3 conv + bn + relu。
4. 在LinearAddBlock和RealVGGBlock中,都有非线性操作bn和relu,只不过在LinearAddBlock的3个分支中没有非线性操作,在RealVGGBlock用一个3x3 conv来代替3个分支,两者后面都接了bn+relu。
LinearAddBlock代码如下,其中scale_conv、scale_1x1和scale_identity表示三个scale常量。在hyper-search阶段,scale_conv和scale_1x1是可训练的变量,在训练目标网络时它们是常量来源自hs训练得到的值。而scale_identity一直都是可训练的变量。此外,scale_conv、scale_1x1的初始化为 \(\sqrt{\frac{2}{l}}\),其中 \(l\) 是block所在的网路层,越深初始化值越小,而scale_identity初始化为1。
# A CSLA block is a LinearAddBlock with is_csla=True
class LinearAddBlock(nn.Module):
def __init__(self, in_channels, out_channels, stride=1, use_post_se=False, is_csla=False, conv_scale_init=None):
super(LinearAddBlock, self).__init__()
self.in_channels = in_channels
self.relu = nn.ReLU()
self.conv = nn.Conv2d(in_channels=in_channels, out_channels=out_channels, kernel_size=3, stride=stride, padding=1, bias=False)
self.scale_conv = ScaleLayer(num_features=out_channels, use_bias=False, scale_init=conv_scale_init)
self.conv_1x1 = nn.Conv2d(in_channels=in_channels, out_channels=out_channels, kernel_size=1, stride=stride, padding=0, bias=False)
self.scale_1x1 = ScaleLayer(num_features=out_channels, use_bias=False, scale_init=conv_scale_init)
if in_channels == out_channels and stride == 1:
self.scale_identity = ScaleLayer(num_features=out_channels, use_bias=False, scale_init=1.0)
self.bn = nn.BatchNorm2d(out_channels)
if is_csla: # Make them constant
self.scale_1x1.requires_grad_(False)
self.scale_conv.requires_grad_(False)
if use_post_se:
self.post_se = SEBlock(out_channels, internal_neurons=out_channels // 4)
else:
self.post_se = nn.Identity()
def forward(self, inputs):
out = self.scale_conv(self.conv(inputs)) + self.scale_1x1(self.conv_1x1(inputs))
if hasattr(self, 'scale_identity'):
out += self.scale_identity(inputs)
out = self.post_se(self.relu(self.bn(out)))
return outRealVGGBlock是训练目标网络时的block,其中用conv替换了LinearAddBlock中的conv、conv_1x1和scale_identity,剩下的bn、relu、se都是一样的。
class RealVGGBlock(nn.Module):
def __init__(self, in_channels, out_channels, stride=1, use_post_se=False):
super(RealVGGBlock, self).__init__()
self.relu = nn.ReLU()
self.conv = nn.Conv2d(in_channels=in_channels, out_channels=out_channels, kernel_size=3, stride=stride, padding=1, bias=False)
self.bn = nn.BatchNorm2d(out_channels)
if use_post_se:
self.post_se = SEBlock(out_channels, internal_neurons=out_channels // 4)
else:
self.post_se = nn.Identity()
def forward(self, inputs):
out = self.post_se(self.relu(self.bn(self.conv(inputs))))
return out在训练目标网络时,我们要用到hs得到的scale常量,代码如下。其中scales_path是hs训练得到的pth权重文件的路径,在函数extract_scales中可以看到这里提取的就是上面LinearAddBlock中的scale_identity、scale_1x1、scale_conv的值。
def extract_scales(model):
blocks = extract_blocks_into_list(model)
scales = []
for b in blocks:
assert isinstance(b, LinearAddBlock)
if hasattr(b, 'scale_identity'):
scales.append((b.scale_identity.weight.detach(), b.scale_1x1.weight.detach(), b.scale_conv.weight.detach()))
else:
scales.append((b.scale_1x1.weight.detach(), b.scale_conv.weight.detach()))
print('extract scales: ', scales[-1][-2].mean(), scales[-1][-1].mean())
return scales
def extract_RepOptVGG_scales_from_pth(num_blocks, width_multiplier, scales_path):
trained_hs_model = RepOptVGG(num_blocks=num_blocks, num_classes=100, width_multiplier=width_multiplier, mode='hs')
weights = torch.load(scales_path, map_location='cpu')
if 'model' in weights:
weights = weights['model']
if 'state_dict' in weights:
weights = weights['state_dict']
for ignore_key in ['linear.weight', 'linear.bias']:
if ignore_key in weights:
weights.pop(ignore_key)
scales = extract_scales(trained_hs_model)
print('check: before loading scales ', scales[-2][-1].mean(), scales[-2][-2].mean())
trained_hs_model.load_state_dict(weights, strict=False)
scales = extract_scales(trained_hs_model)
print('========================================== loading scales from', scales_path)
print('check: after loading scales ', scales[-2][-1].mean(), scales[-2][-2].mean())
return scale在构建好目标网络并从hs阶段训练的权重中提取出所需要的常量scale值后,还需要进行两步,第一步是按式(7)23初始化目标网络的权重,第二步就是重构optimizer,其中需要根据hs搜索得到的scale值来计算Grad Mult tensor,然后在每个optimizer().step()乘以Grad Mult。代码如下
def build_RepOptVGG_SGD_optimizer(model, scales, lr, momentum=0.9, weight_decay=4e-5):
from optimizer import set_weight_decay
handler = RepOptVGGHandler(model, scales, reinit=True, update_rule='sgd')
handler.reinitialize()
params = set_weight_decay(model)
optimizer = RepOptimizerSGD(handler.generate_grad_mults(), params, lr=lr,
momentum=momentum, weight_decay=weight_decay, nesterov=True)
return optimizer其中RepOptVGGHandler定义了初始化目标网络权重函数reinitialize()和计算Grad Mult tensor的函数generate_grad_mults()。
class RepOptVGGHandler(RepOptimizerHandler):
# scales is a list, scales[i] is a triple (scale_identity.weight, scale_1x1.weight, scale_conv.weight) or
# a two-tuple (scale_1x1.weight, scale_conv.weight) (if the block has no scale_identity)
def __init__(self, model, scales,
reinit=True, use_identity_scales_for_reinit=True,
cpu_mode=False,
update_rule='sgd'):
blocks = extract_blocks_into_list(model)
convs = [b.conv for b in blocks]
assert update_rule in ['sgd', 'adamw'] # Currently supports two update functions
self.update_rule = update_rule
self.model = model
self.scales = scales
self.convs = convs
self.reinit = reinit
self.use_identity_scales_for_reinit = use_identity_scales_for_reinit
self.cpu_mode = cpu_mode
def reinitialize(self):
if self.reinit:
for m in self.model.modules():
if isinstance(m, nn.BatchNorm2d):
gamma_init = m.weight.mean()
if gamma_init == 1.0:
print('Checked. This is training from scratch.')
else:
raise Warning('========================== Warning! Is this really training from scratch? =================')
print('##################### Re-initialize #############')
for scale, conv3x3 in zip(self.scales, self.convs):
in_channels = conv3x3.in_channels
out_channels = conv3x3.out_channels
kernel_1x1 = nn.Conv2d(in_channels, out_channels, 1)
if len(scale) == 2:
conv3x3.weight.data = conv3x3.weight * scale[1].view(-1, 1, 1, 1) \
+ F.pad(kernel_1x1.weight, [1, 1, 1, 1]) * scale[0].view(-1, 1, 1, 1)
else:
assert len(scale) == 3
assert in_channels == out_channels
identity = torch.eye(out_channels).reshape(out_channels, out_channels, 1, 1)
conv3x3.weight.data = conv3x3.weight * scale[2].view(-1, 1, 1, 1) + F.pad(kernel_1x1.weight,
[1, 1, 1, 1]) * scale[1].view(-1, 1, 1, 1)
if self.use_identity_scales_for_reinit: # You may initialize the imaginary CSLA block with the trained identity_scale values. Makes almost no difference.
identity_scale_weight = scale[0]
conv3x3.weight.data += F.pad(identity * identity_scale_weight.view(-1, 1, 1, 1), [1, 1, 1, 1])
else:
conv3x3.weight.data += F.pad(identity, [1, 1, 1, 1])
else:
raise Warning('========================== Warning! Re-init disabled. Guess you are doing an ablation study? =================')
def generate_grad_mults(self):
grad_mult_map = {}
if self.update_rule == 'sgd':
power = 2
else:
power = 1
for scales, conv3x3 in zip(self.scales, self.convs):
para = conv3x3.weight
if len(scales) == 2:
mask = torch.ones_like(para) * (scales[1] ** power).view(-1, 1, 1, 1)
mask[:, :, 1:2, 1:2] += torch.ones(para.shape[0], para.shape[1], 1, 1) * (scales[0] ** power).view(-1, 1, 1, 1)
else:
mask = torch.ones_like(para) * (scales[2] ** power).view(-1, 1, 1, 1)
mask[:, :, 1:2, 1:2] += torch.ones(para.shape[0], para.shape[1], 1, 1) * (scales[1] ** power).view(-1, 1, 1, 1)
ids = np.arange(para.shape[1])
assert para.shape[1] == para.shape[0]
mask[ids, ids, 1:2, 1:2] += 1.0
if self.cpu_mode:
grad_mult_map[para] = mask
else:
grad_mult_map[para] = mask.cuda()
return grad_mult_map而RepOptimizerSGD继承了torch.optim.sgd.SGD,并在更新权重时原本的梯度乘以grad_mult。
class RepOptimizerSGD(SGD):
def __init__(self,
grad_mult_map,
params,
lr, momentum=0, dampening=0,
weight_decay=0, nesterov=False):
super(RepOptimizerSGD, self).__init__(params, lr, momentum, dampening=dampening, weight_decay=weight_decay, nesterov=nesterov)
self.grad_mult_map = grad_mult_map
print('============ Grad Mults generated. There are ', len(self.grad_mult_map))
def step(self, closure=None):
loss = None
if closure is not None:
loss = closure()
for group in self.param_groups:
weight_decay = group['weight_decay']
momentum = group['momentum']
dampening = group['dampening']
nesterov = group['nesterov']
for p in group['params']:
if p.grad is None:
continue
if p in self.grad_mult_map:
d_p = p.grad.data * self.grad_mult_map[p] # Note: multiply here
else:
d_p = p.grad.data
if weight_decay != 0:
d_p.add_(p.data, alpha=weight_decay)
if momentum != 0:
param_state = self.state[p]
if 'momentum_buffer' not in param_state:
buf = param_state['momentum_buffer'] = torch.clone(d_p).detach()
else:
buf = param_state['momentum_buffer']
buf.mul_(momentum).add_(d_p, alpha=1 - dampening)
if nesterov:
d_p = d_p + buf * momentum # d_p.add(buf, momentum)
else:
d_p = buf
p.data.add_(d_p, alpha=-group['lr'])
return loss