LeetCode题练习与总结：从前序与中序遍历序列构造二叉树--105

news2024/11/19 19:23:59

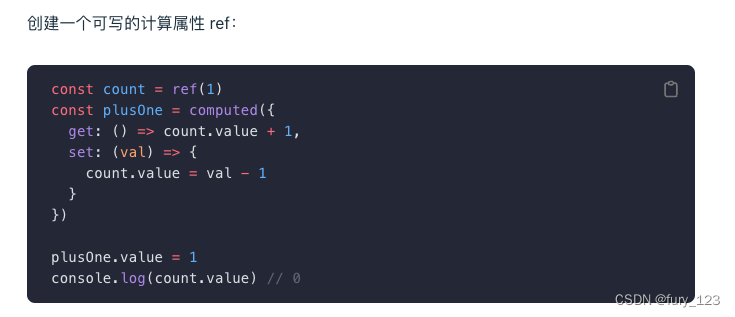
一、题目描述

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例 1:

输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

示例 2:

输入: preorder = [-1], inorder = [-1]
输出: [-1]

提示:

1 <= preorder.length <= 3000
inorder.length == preorder.length
-3000 <= preorder[i], inorder[i] <= 3000
preorder 和 inorder 均 无重复 元素
inorder 均出现在 preorder
preorder 保证为二叉树的前序遍历序列
inorder 保证为二叉树的中序遍历序列

二、解题思路

这个问题是关于如何根据给定的先序遍历和中序遍历数组来重建二叉树。我们可以使用递归方法来解决这个问题。

算法步骤：

首先，在先序遍历数组preorder中找到根节点的值。
然后，在inorder数组中找到根节点的值，并以此为界将inorder数组分为左右两部分。
递归地构造左子树和右子树。
左子树的preorder数组为preorder数组中根节点后面的所有值，左子树的inorder数组为inorder数组中左子树部分的所有值。
右子树的preorder数组为preorder数组中根节点后面的所有值，右子树的inorder数组为inorder数组中右子树部分的所有值。
重复上述步骤，直到所有节点都被处理。

三、具体代码

class Solution {
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        if (preorder == null || inorder == null) {
            return null;
        }
        return helper(preorder, 0, preorder.length - 1, inorder, 0, inorder.length - 1);
    }

    private TreeNode helper(int[] preorder, int preorderStart, int preorderEnd, int[] inorder, int inorderStart, int inorderEnd) {
        if (preorderStart > preorderEnd || inorderStart > inorderEnd) {
            return null;
        }
        int rootVal = preorder[preorderStart];
        TreeNode root = new TreeNode(rootVal);
        int index = inorderStart;
        while (index <= inorderEnd && inorder[index] != rootVal) {
            index++;
        }
        int leftSubtreeSize = index - inorderStart;
        int rightSubtreeSize = inorderEnd - index;
        root.left = helper(preorder, preorderStart + 1, preorderStart + leftSubtreeSize, inorder, inorderStart, index - 1);
        root.right = helper(preorder, preorderStart + leftSubtreeSize + 1, preorderEnd, inorder, index + 1, inorderEnd);
        return root;
    }
}

四、时间复杂度和空间复杂度

1. 时间复杂度

helper 函数对于每个节点都会被调用一次，其中 n 是树中节点的数量。
在 helper 函数内部，对于每个节点，我们都会进行一次数组查找（index 循环），这需要 O(1) 的时间。
因此，总的时间复杂度是 O(n)。

2. 空间复杂度

空间复杂度主要取决于递归调用栈的深度，这通常与树的高度 h 有关。
在最坏的情况下，树是完全不平衡的，例如每个节点都只有左子节点或者只有右子节点，此时树的高度等于节点的数量，空间复杂度为 O(n)。
在最好的情况下，树是完全平衡的，此时树的高度为 log(n)，空间复杂度为 O(log(n))。
因此，空间复杂度在 O(log(n)) 到 O(n) 之间，取决于树的形状。

综上所述，代码的时间复杂度是 O(n)，空间复杂度在 O(log(n)) 到 O(n) 之间，取决于树的形状。

五、总结知识点

递归：代码使用了递归的方法来构建二叉树。递归是一种分而治之的算法技巧，将复杂问题分解为更小的子问题，并逐个解决。
二叉树：代码操作的是二叉树数据结构，这是一种每个节点最多有两个子节点的树形结构。
先序遍历和中序遍历：先序遍历是指根节点、左子树、右子树的顺序，中序遍历是指左子树、根节点、右子树的顺序。这两个遍历顺序是构建二叉树的关键信息来源。
数组操作：代码中使用了数组操作来找到根节点在先序和中序遍历中的位置，并以此构建左右子树。
函数返回值：buildTree 函数返回构建的二叉树的根节点，而 helper 函数返回当前节点的子节点。
节点定义：代码中使用了 TreeNode 类来定义二叉树的节点，每个节点包含一个整数值和指向左右子节点的引用。
递归的基本情况：递归函数通常有一个基本情况（base case），即递归退出的条件。在这个问题中，基本情况是当 preorderStart > preorderEnd 或 inorderStart > inorderEnd 时，表示没有更多的节点可以处理，此时返回 null。
类型转换：在递归调用中，buildTree 函数的返回值被隐式转换为 TreeNode 类型。
递归调用栈：递归函数的调用会形成调用栈，用于存储每一层递归调用的局部变量和返回地址。
树的高度与深度：在二叉树中，根节点的深度为1，每个子节点的深度是其父节点深度加1。树的高度是从根节点到最远叶子节点的最长路径上的节点数。