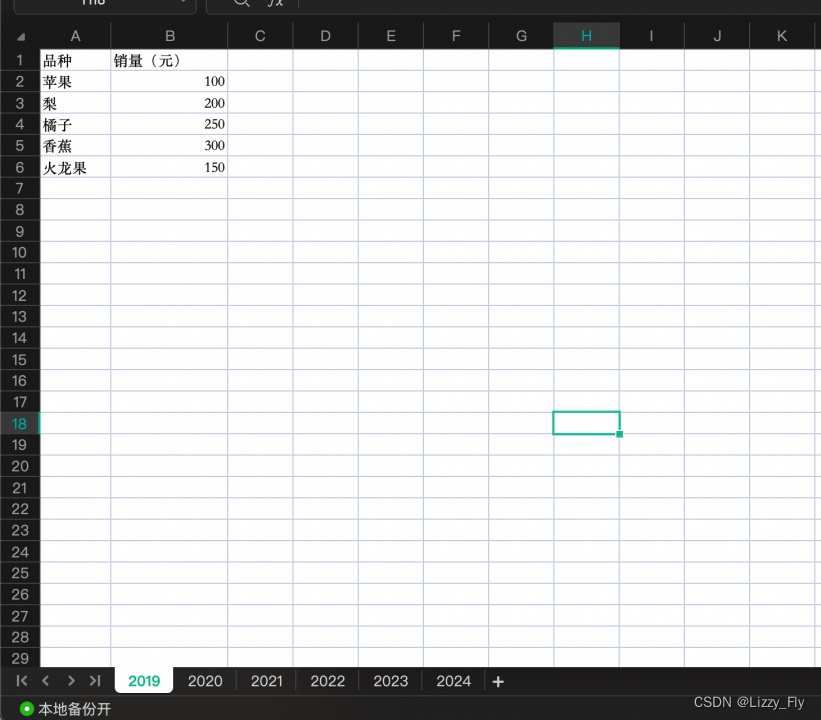
一个水果销量表,Excel包含多个年份sheet,需要提取某个品种的水果每年的销量,看看几个AI的分析结果吧
1、文心一言3.5(不支持Excel)
不支持上传Excel文件

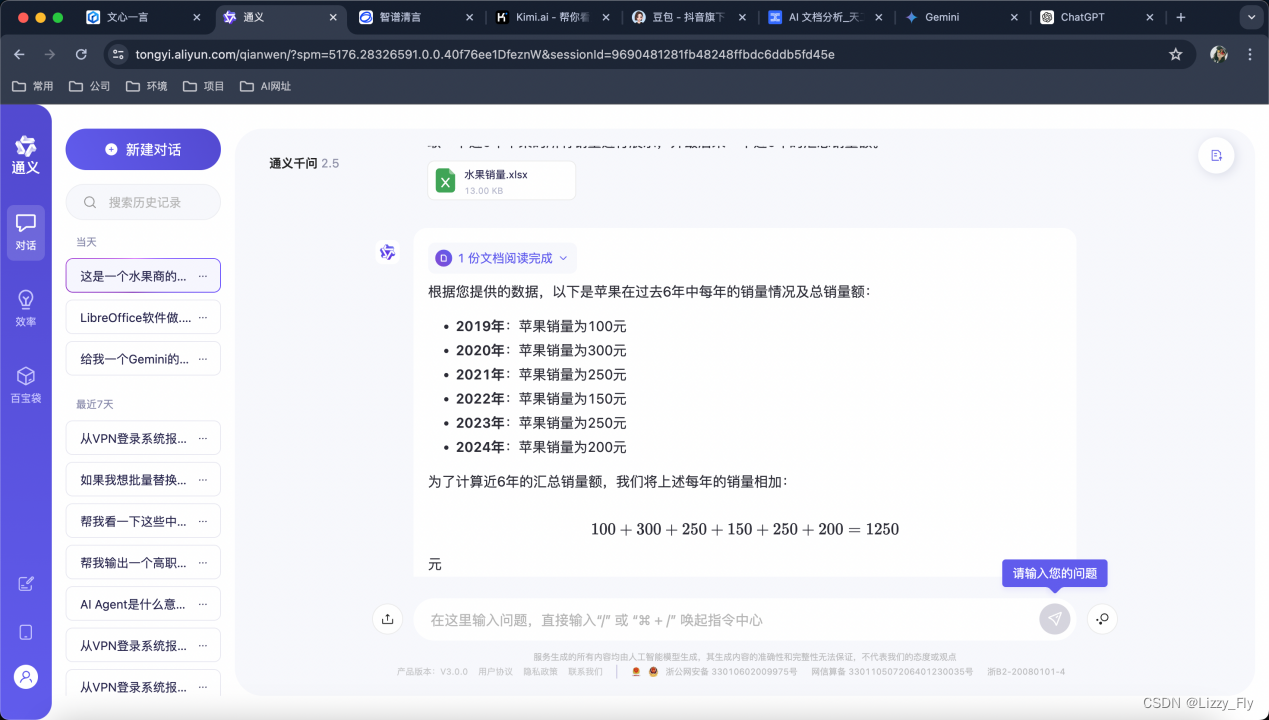
2、 通义千问2.5(完成★)
顺利完成分析,但没有后续分析推荐
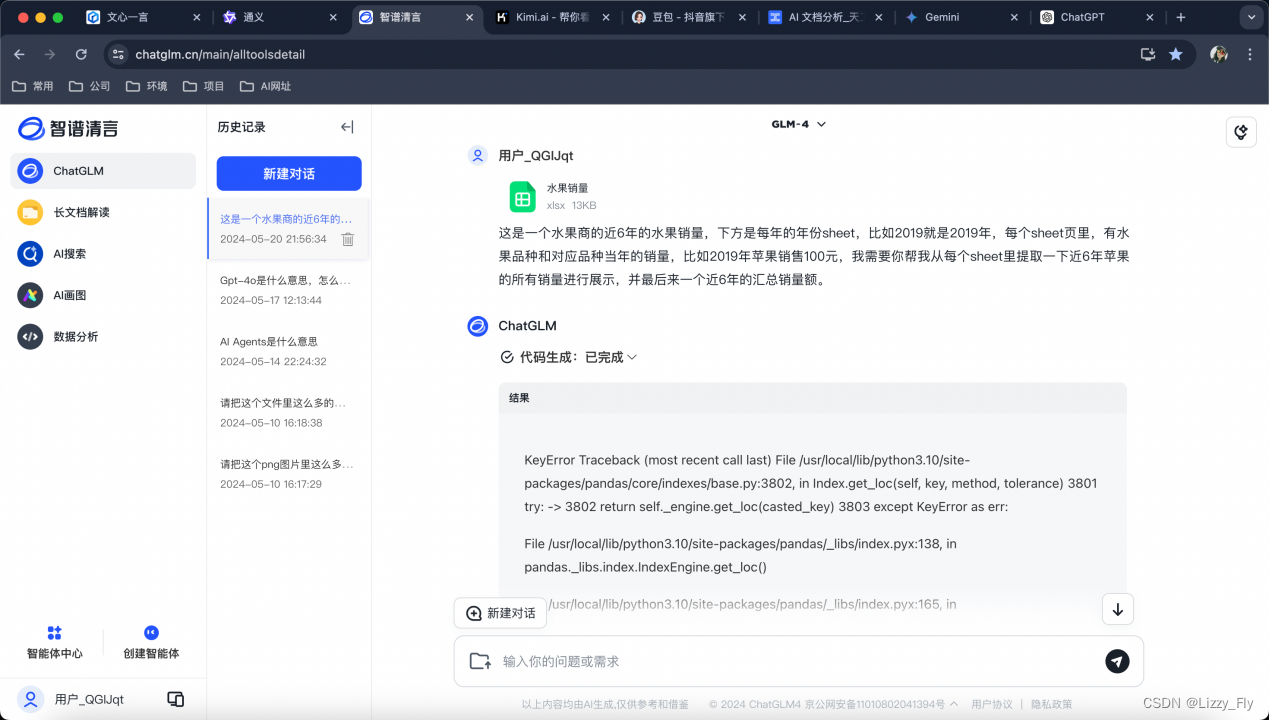
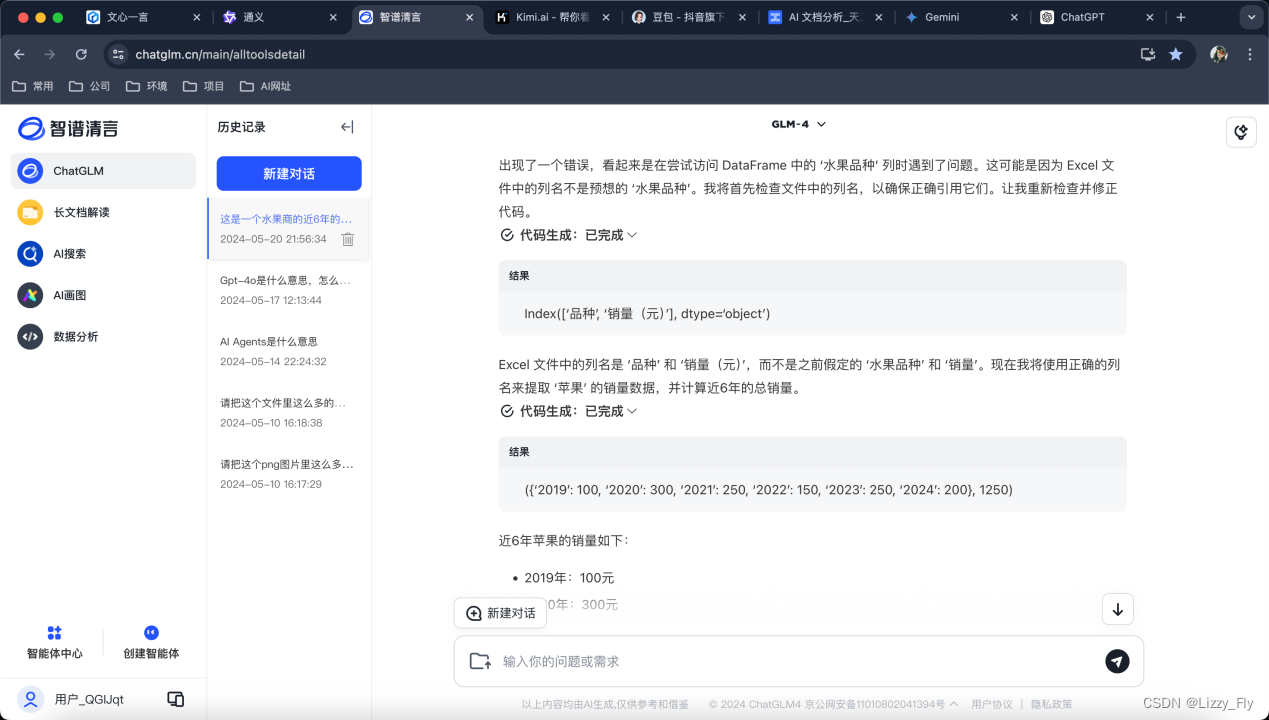
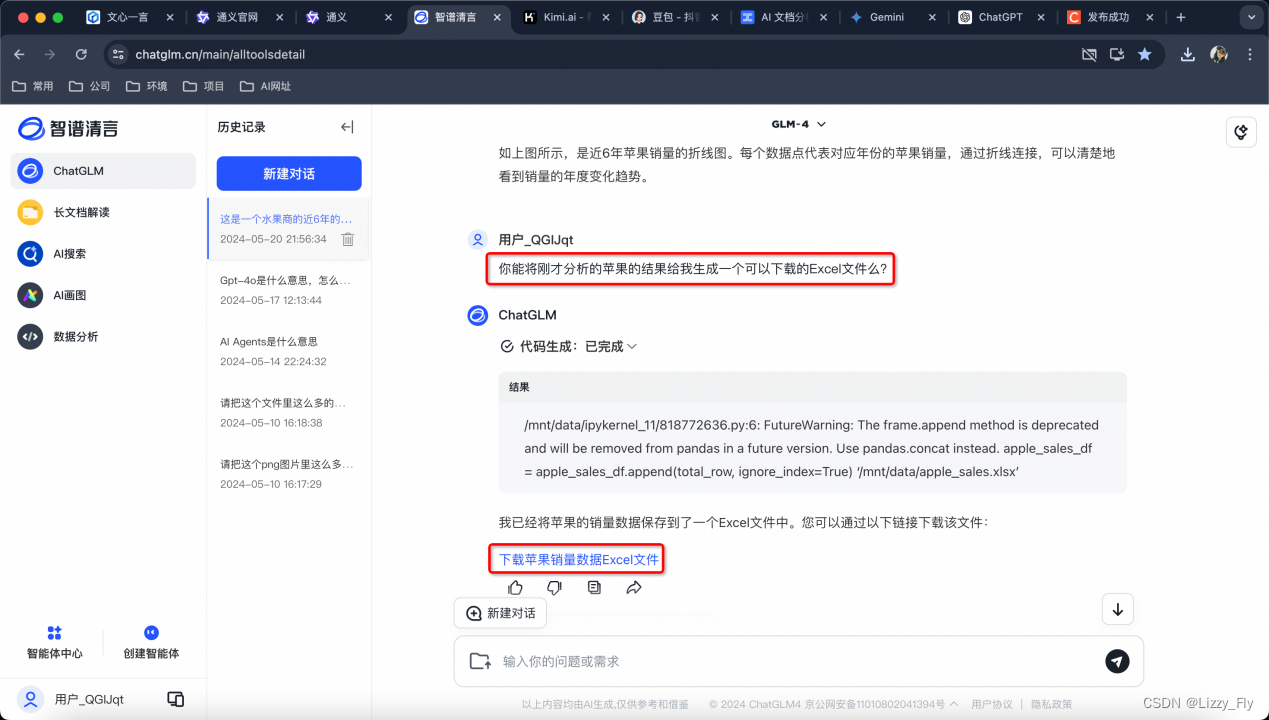
3、智谱清言GML-4(优质★★★★★)
最优质的输出结果,完全能提取展示数据,并有后续推荐和图表生成
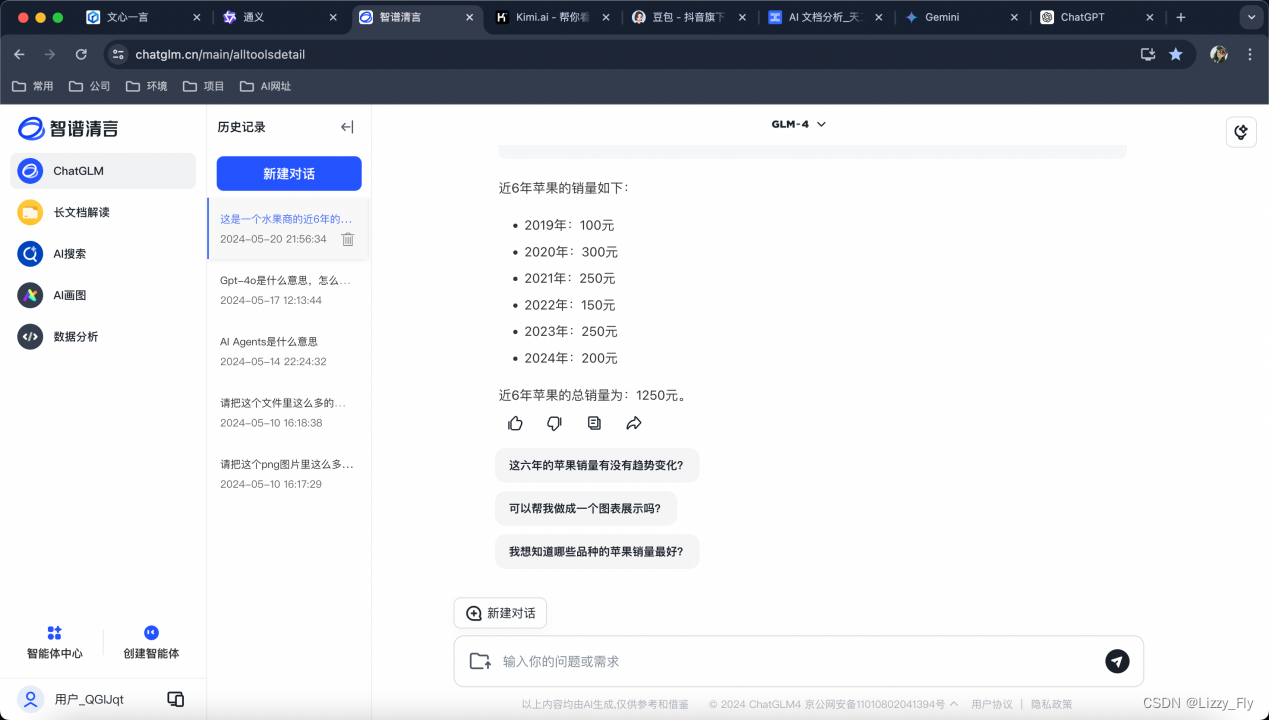
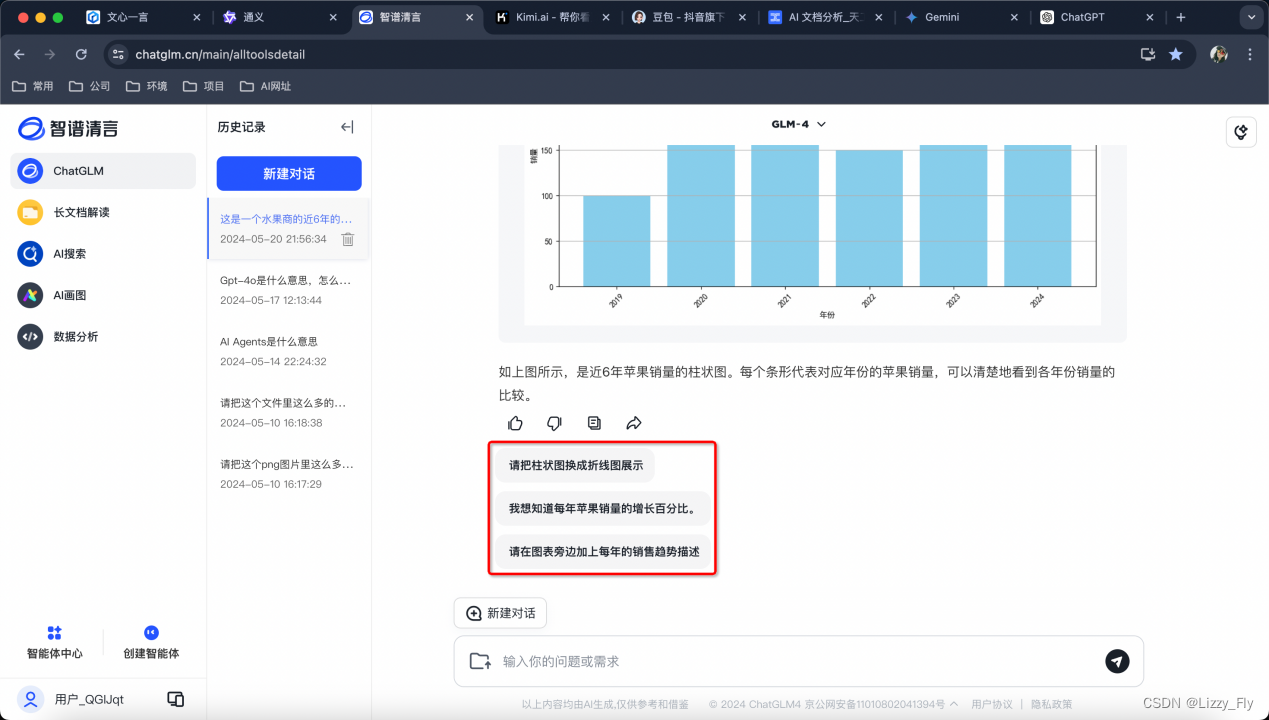
还有各类续写提示
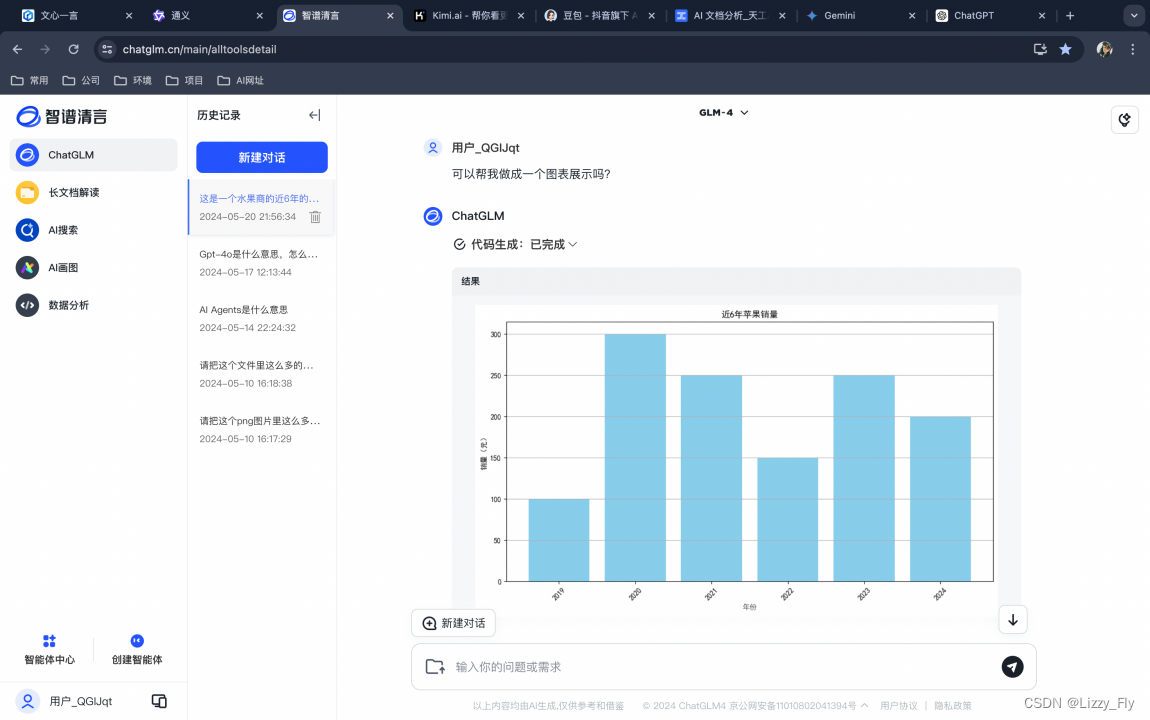
可以做图表展示
Excel分析者的福音
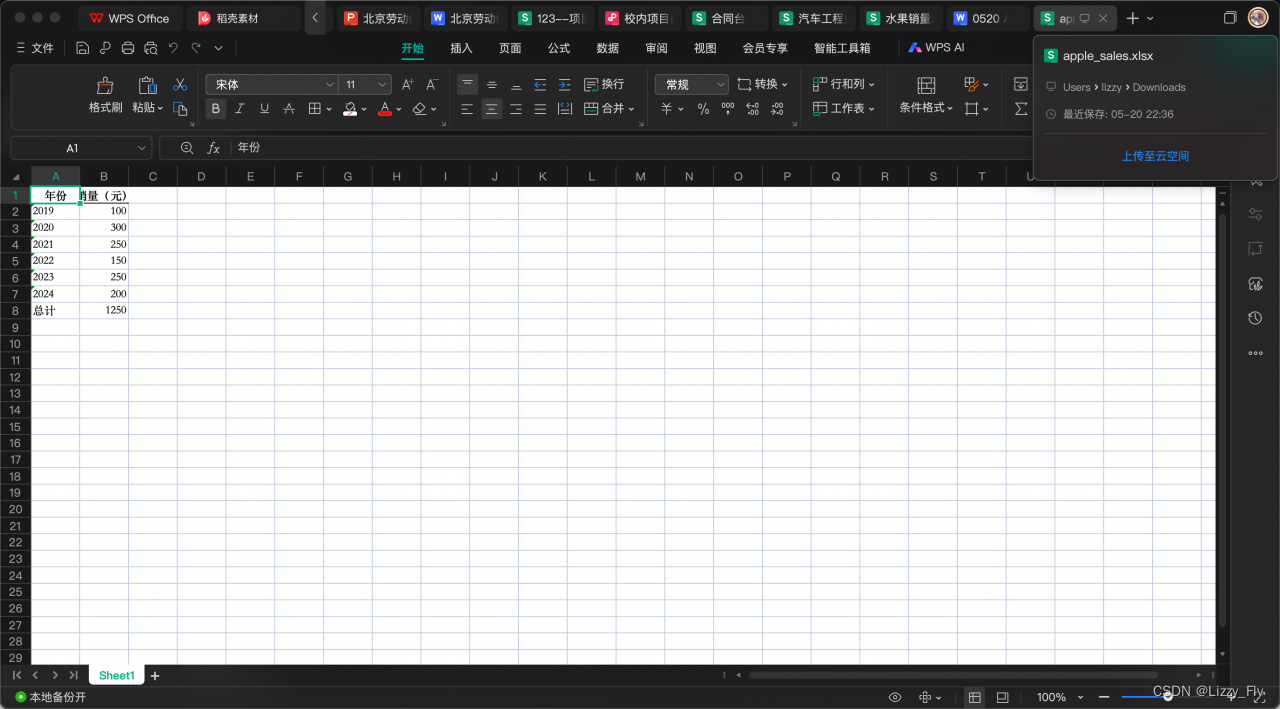
并且针对分析结果可以生成可下载的Excel文件
4、Kimi(离谱:支持Excel,却不能分析sheet)
无法解读Excel文件,但文件上传里支持xlsx

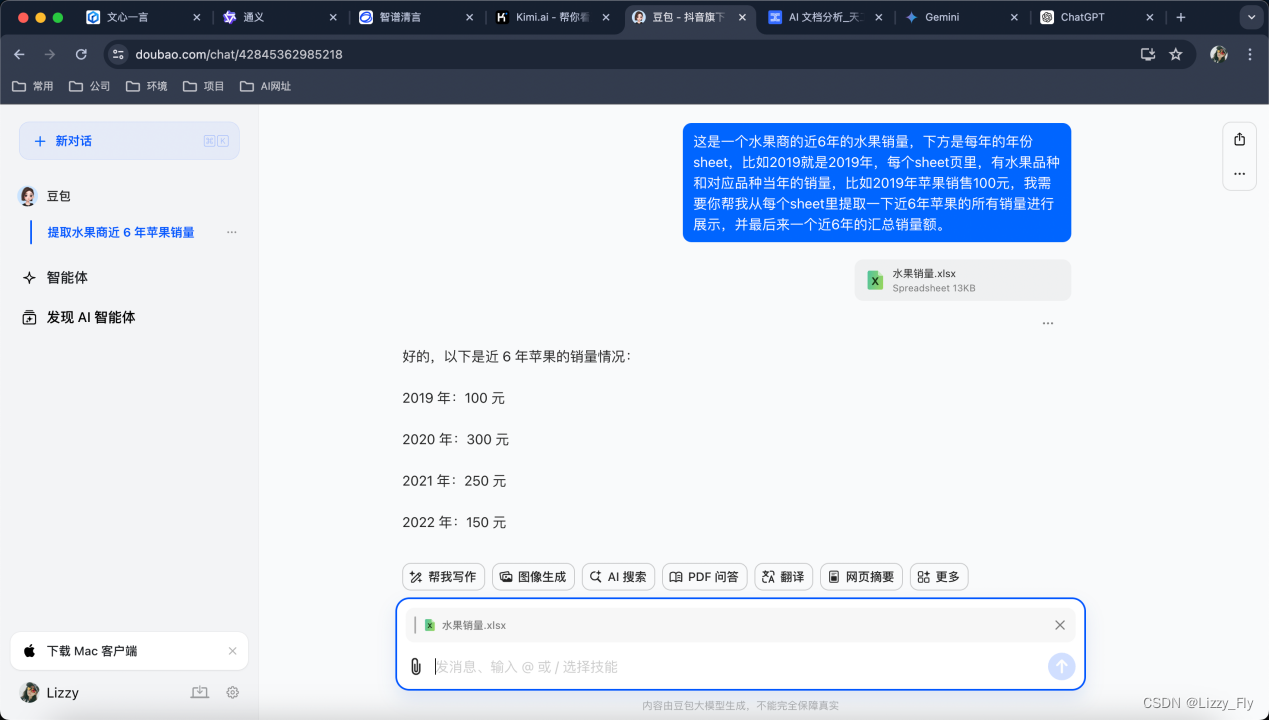
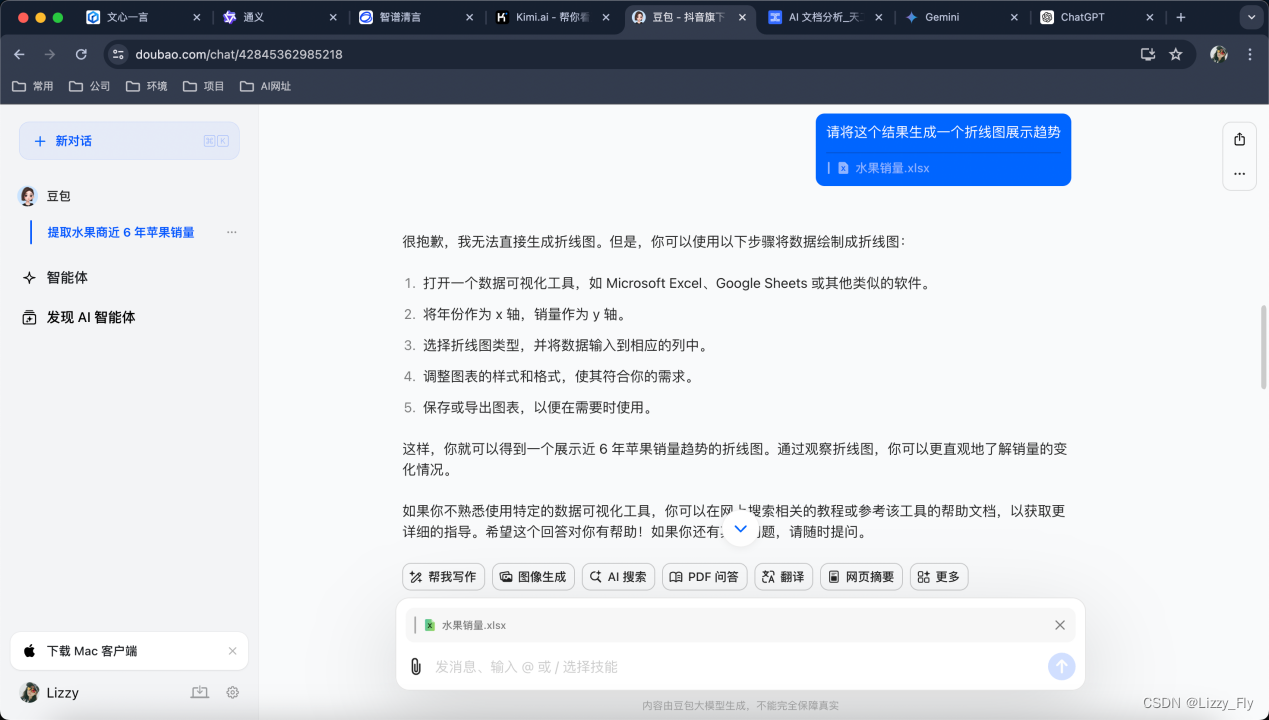
5、豆包(完成★★★)
可以分析出想要的结果,而且有后续分析推荐,但不能生成图表展示
也有续写
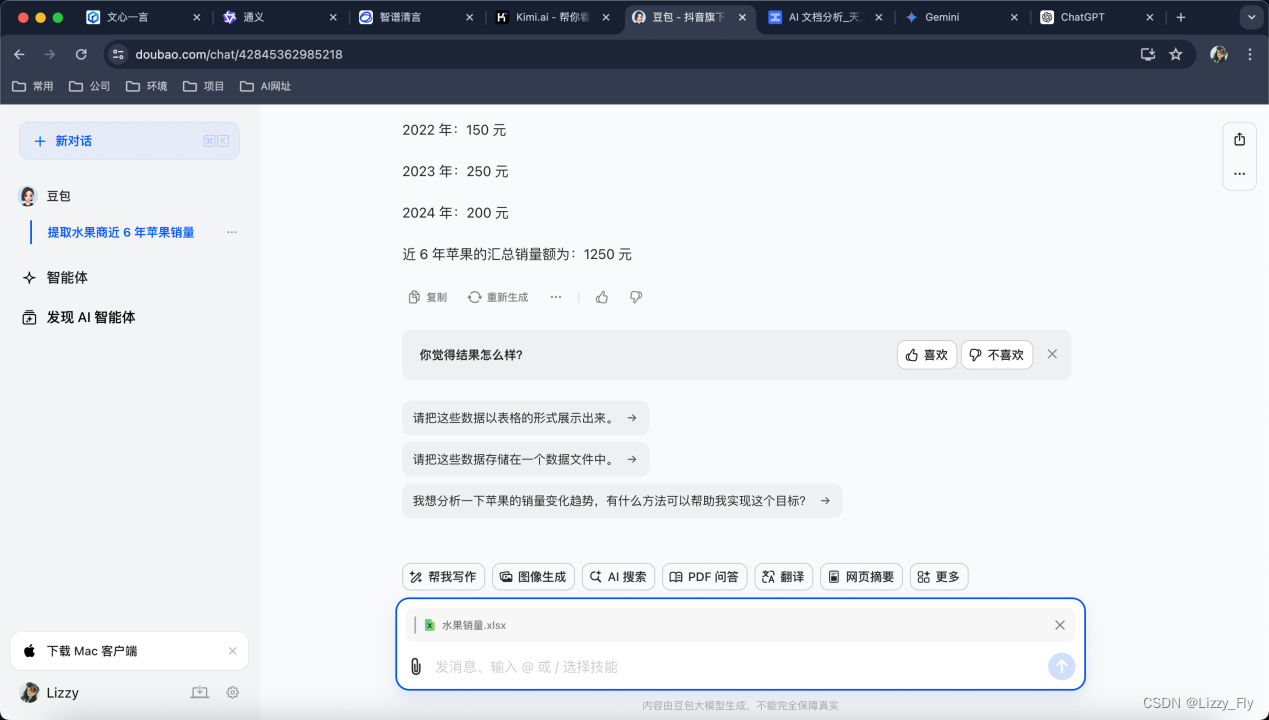
但不能生成折线图柱状图等图表
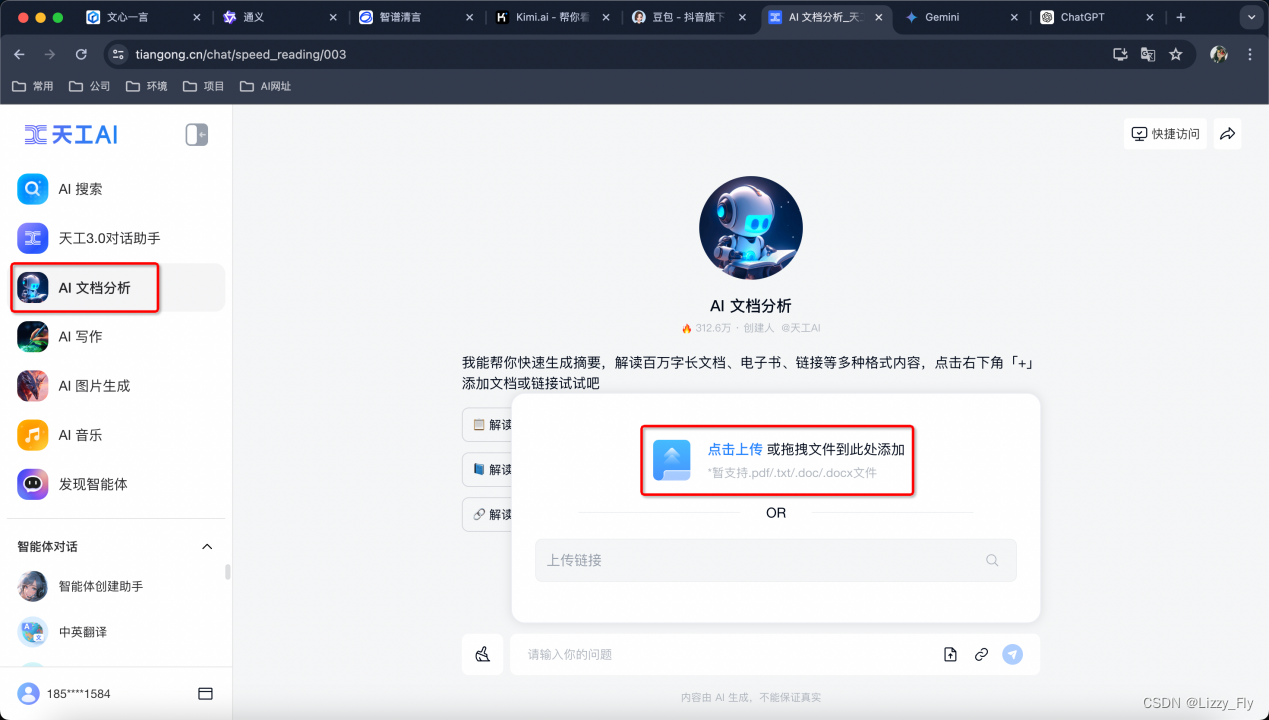
6、天工AI(不支持Excel)
文档分析都不支持Excel
7、Gemini(不支持Excel,只支持图片)

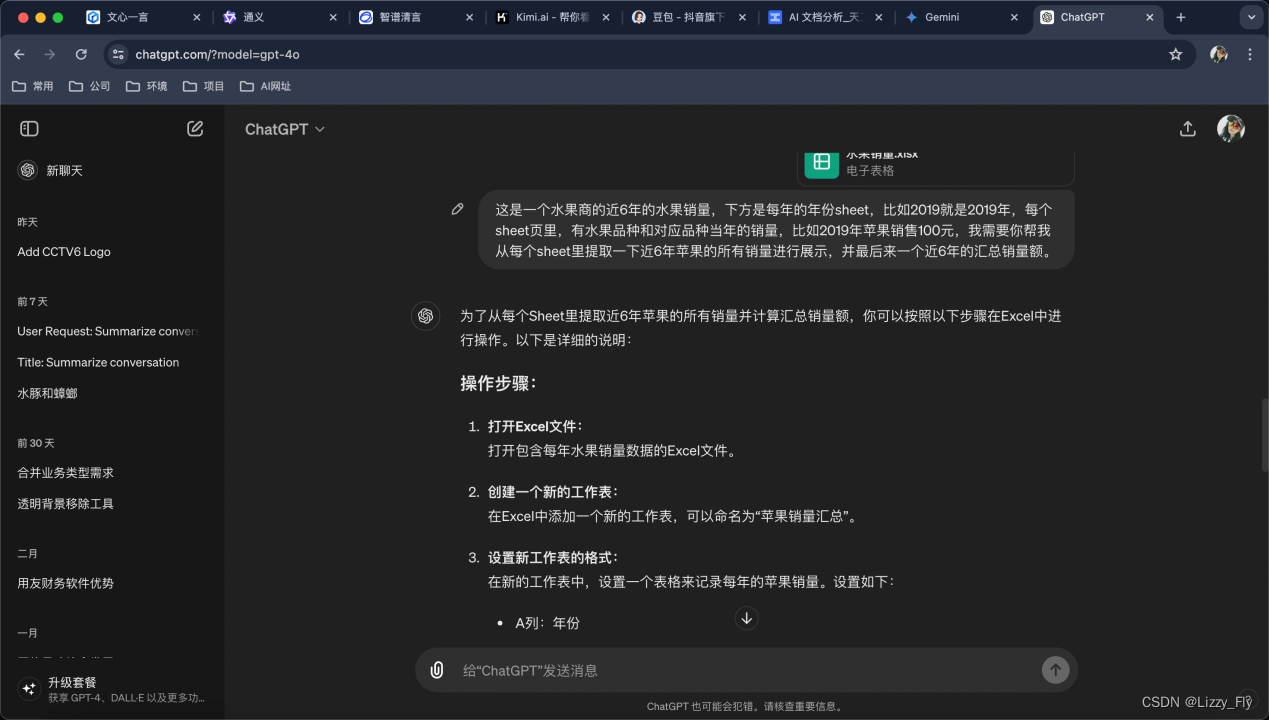
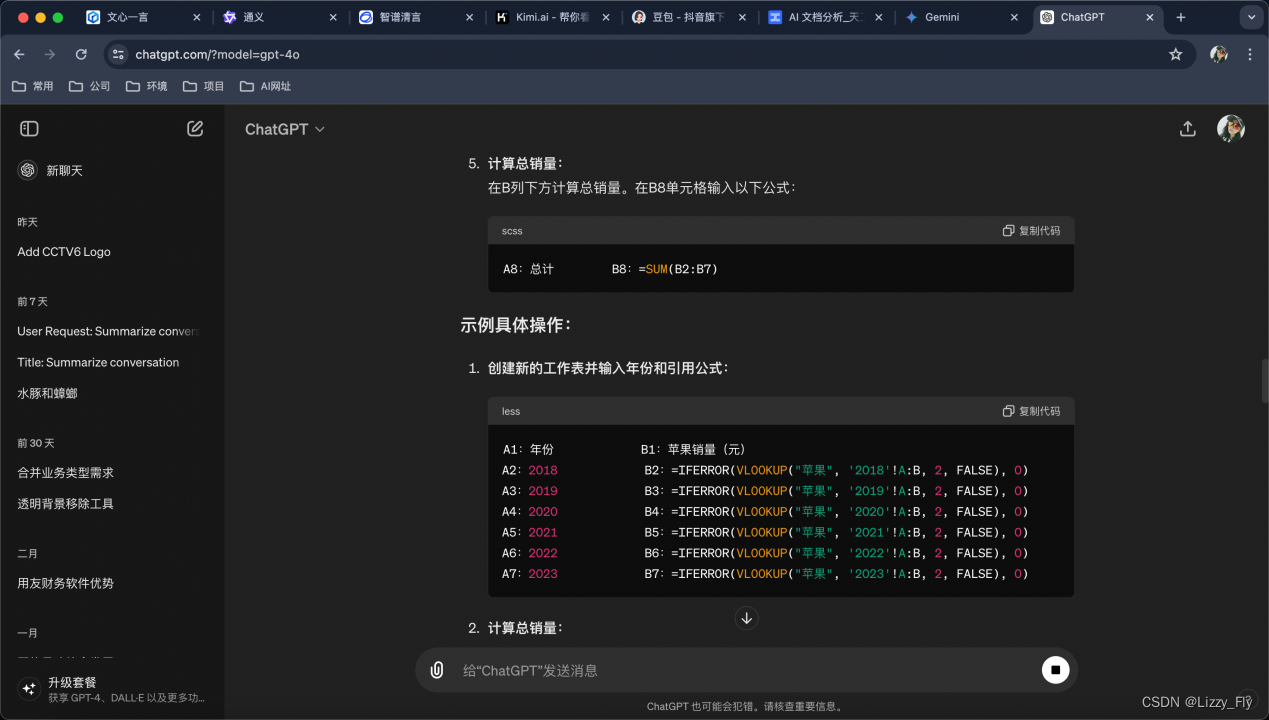
8、ChatGPT-4o(失败)
9、总结:
1)第一名-智谱清言:Excel简单的分析,最好的是智谱清言,能正确提取数据,并有相关后续分析建议,且能生成图标分析结果进行展示,而且针对分析结果可以生成可下载的Excel文件。
2)第二名-豆包:可以分析出结果,而且会提出对应后续的建议,但不支持生成图表
3)第三名-通义千问:可以分析出结果,但没有后续的分析建议,无法给提问者发散分析思维,体验不佳
4)其他分析失败:文心一言、kimi、天工AI、Gemini、ChatGPT-4o
10、网址链接:
1)文心一言:https://yiyan.baidu.com/
2)通义千问:https://tongyi.aliyun.com/qianwen/
3)智谱清言:https://chatglm.cn/main/alltoolsdetail
4)Kimi:https://kimi.moonshot.cn/chat/cp5ld5hp2k15mqsqh0mg
5)豆包:https://www.doubao.com/chat/
6)天工AI:https://www.tiangong.cn/chat/
7)Gemini:https://gemini.google.com
8)ChatGPT:https://chatgpt.com/?model=gpt-4o



![[面试题]软件测试性能测试的常见指标在Linux系统中,一个文件的访问权限是 755,其含义是什么](https://img-blog.csdnimg.cn/direct/1a33e1c1502848d8b1d2f4ebbb7d1b80.png)