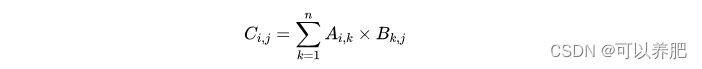K-means算法是一种常见的聚类算法，用于将数据点分成不同的组（簇），使同一组内的数据点彼此相似，不同组之间的数据点相对较远。以下是K-means算法的基本工作原理和步骤：

工作原理：

初始化：选择K个初始聚类中心点（质心）。
分配：将每个数据点分配到最接近的聚类中心，形成K个簇。
更新：根据每个簇中的数据点重新计算聚类中心。
迭代：重复步骤2和3，直到满足停止条件（如聚类中心不再改变或达到最大迭代次数）。

算法步骤：

初始化：随机选择K个数据点作为初始聚类中心。
分配：对于每个数据点，计算其与各个聚类中心的距离，将其分配给距离最近的聚类中心。
更新：重新计算每个簇的聚类中心，使用该簇内所有数据点的平均值。
迭代：重复步骤2和3，直到聚类中心稳定或达到最大迭代次数。

优点：

简单且高效，适用于大规模数据集。
对于球状簇具有很好的效果，易于解释。

缺点：

需要预先设定聚类数K。
对异常值和噪声敏感。
结果可能受初始聚类中心的选择影响。

应用领域：

图像分割、文本聚类、市场分析、推荐系统等。

实现聚类分析的基本步骤如下：

数据准备与预处理：

读取数据：从Excel文件中读取数据，对数据进行去重和缺失值处理。
特征选择：选择用于聚类分析的特征列，如'地区发展程度'、'时间间隔'、'评论回复数'、'评论点赞数'等。

df.drop_duplicates(subset=['评论'], keep='first', inplace=True)
df.dropna(subset=['评论'],axis=0,inplace=True)
# 将评论时间列转换为时间格式
df['评论时间'] = pd.to_datetime(df['评论时间'])
# 计算每个时间点距禖当前时间的时间间隔（单位：秒）
current_time = datetime.now()
df['时间间隔'] = round((current_time - df['评论时间']).dt.total_seconds().astype(int)/86400,1)
print(df.info())
# 创建一个字典，用于映射地区与发展水平的关系
region_mapping = {
    '发达地区': ['北京省', '上海省', '天津省', '上海省'],
    '普通地区': ['广东省', '江苏省', '浙江省', '福建省', '湖北省', '湖南省', '安徽省', '江西省', '山东省', '辽宁省', '吉林省', '黑龙江省'],
    '发展地区': ['重庆省', '河南省', '四川省', '陕西省', '天津省', '山西省', '内蒙古省', '河北省', '广西省', '海南省', '河南省', '河北省', '山西省', '内蒙古省', '宁夏省', '青海省', '甘肃省',
             '陕西省', '新疆省'],
    '未知': ['设置了隐私'],
}

数据标准化：

使用StandardScaler对特征数据进行标准化，使数据具有零均值和单位方差。

scaler = StandardScaler()
X_data = scaler.fit_transform(X_data)

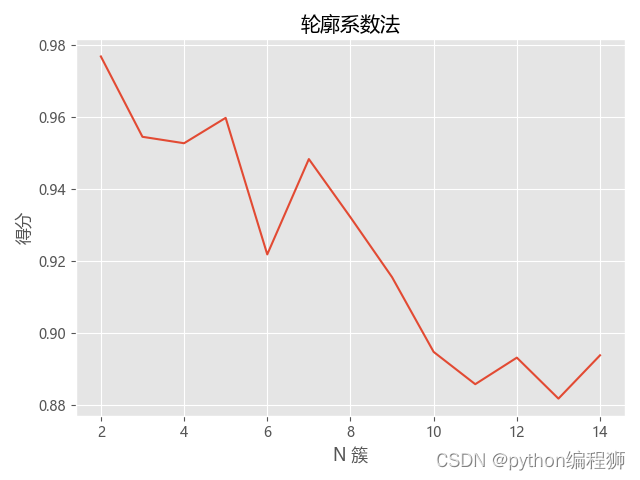
确定聚类数目：

使用“肘部法”和“轮廓系数法”等方法确定合适的聚类数目。

# 构造自定义函数，用于绘制不同k值和对应总的簇内离差平方和的折线图
def k_SSE(X, clusters):
    # 选择连续的K种不同的值
    K = range(1, clusters + 1)
    # 构建空列表用于存储总的簇内离差平方和
    TSSE = []
    for k in K:
        # 用于存储各个簇内离差平方和
        SSE = []
        kmeans = KMeans(n_clusters=k)
        kmeans.fit(X)
        # 返回簇标签
        labels = kmeans.labels_
        # 返回簇中心
        centers = kmeans.cluster_centers_
        # 计算各簇样本的离差平方和，并保存到列表中
        for label in set(labels):
            SSE.append(np.sum((X[labels == label, :] - centers[label, :]) ** 2))
        # 计算总的簇内离差平方和
        TSSE.append(np.sum(SSE))

    # 中文和负号的正常显示
    plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
    plt.rcParams['axes.unicode_minus'] = False
    # 设置绘图风格
    plt.style.use('ggplot')
    # 绘制K的个数与GSSE的关系
    plt.plot(K, TSSE, 'b*-')
    plt.xlabel('簇的个数')
    plt.ylabel('簇内离差平方和之和')
    plt.title('手肘法')
    # 显示图形
    plt.show()

聚类分析：

使用自定义的KMeans类或Sklearn中的KMeans进行聚类分析，传入特征数据和确定的聚类数目。
获取聚类标签并将其与特征数据关联。

n_clusters = 5
km = KMeans(n_clusters=n_clusters).fit(X_data)

#% 降维后画图显示聚类结果
#将原始数据中的索引设置成得到的数据类别
X_rsl = pd.DataFrame(X_data,index=km.labels_)
X_rsl_center = pd.DataFrame(km.cluster_centers_) #找出聚类中心

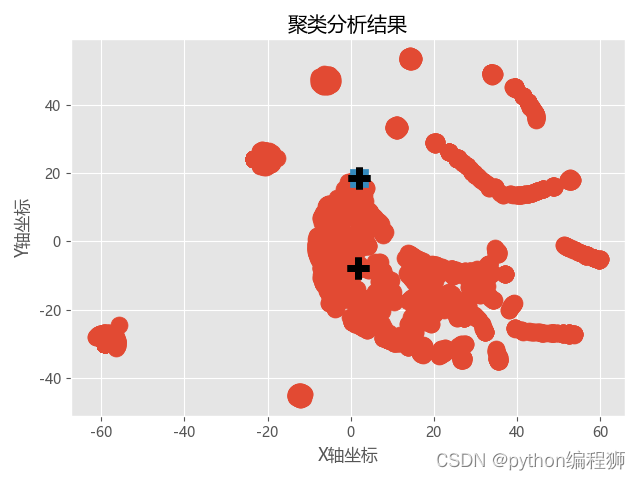
降维可视化：

使用TSNE对聚类结果进行降维处理，将高维数据降至二维或三维。
利用降维后的数据和聚类中心绘制散点图，根据聚类结果进行着色展示。

tsne = TSNE()
tsne.fit_transform(X_rslwithcenter) #进行数据降维,并返回结果

结果输出：

将聚类标签与原始数据关联，将聚类结果输出到Excel文件中。