目录
- 1.不同路径
- 1.题目链接
- 2.算法原理详解
- 3.代码实现
- 2.不同路径 II
- 1.题目链接
- 2.算法原理详解
- 3.代码实现
- 3.珠宝的最高价值
- 1.题目链接
- 2.算法原理详解
- 3.代码实现
1.不同路径
1.题目链接
- 不同路径
2.算法原理详解
- 思路:
-
确定状态表示 ->
dp[i][j]的含义- 走到
dp[i][j]的时候,一共有多少种方式
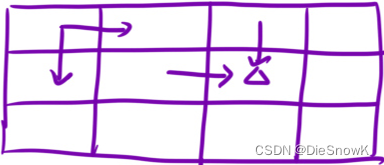
- 走到
-
推导状态转移方程
dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
-
初始化:
dp表多开一行和一列虚拟结点,避免处理边界dp[0][1] = 1 || dp[1][0] = 1

-
确定填表顺序:从上往下,从左往右
-
确定返回值:
dp[n][m]
-
- 上述如果
dp表不多开那一行和一列虚拟结点会怎么样?- 需要做边界处理,将第一列和第一行先初始化为1
3.代码实现
int uniquePaths(int n, int m)
{
vector<vector<int>> dp(n + 1, vector<int>(m + 1, 0));
dp[0][1] = 1;
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= m; j++)
{
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[n][m];
}
2.不同路径 II
1.题目链接
- 不同路径 II
2.算法原理详解
- 思路:
-
确定状态表示 ->
dp[i][j]的含义- 走到
dp[i][j]的时候,一共有多少种方式
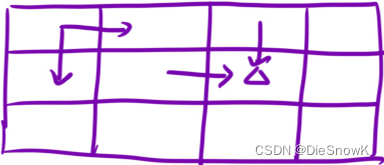
- 走到
-
推导状态转移方程
dp[i][j] = dp[i - 1][j] + dp[i][j - 1]

-
初始化:
dp表多开一行和一列虚拟结点,避免处理边界dp[0][1] = 1 || dp[1][0] = 1
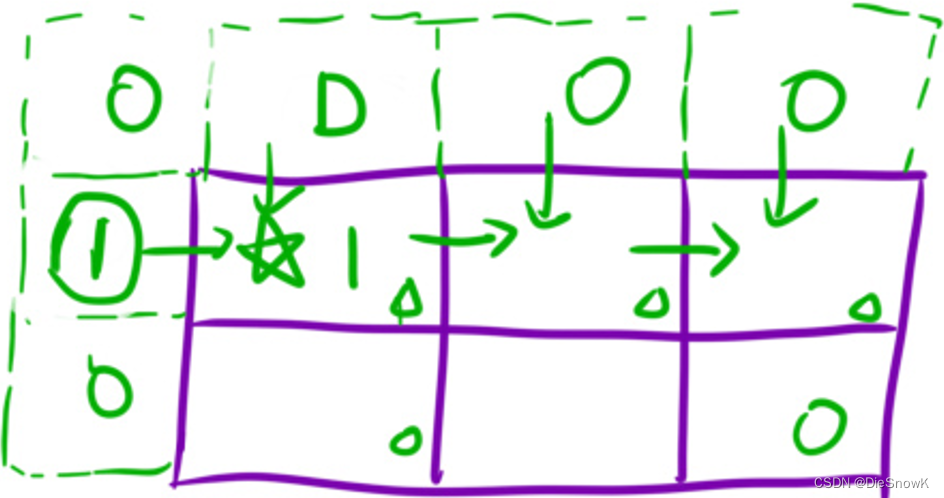
-
确定填表顺序:从上往下,从左往右
-
确定返回值:
dp[n][m]
-
3.代码实现
int uniquePathsWithObstacles(vector<vector<int>>& ob)
{
int n = ob.size(), m = ob[0].size();
vector<vector<int>> dp(n + 1, vector<int>(m + 1, 0));
dp[0][1] = 1;
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= m; j++)
{
if(ob[i - 1][j - 1] == 0) // 注意下表映射关系
{
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
}
return dp[n][m];
}
3.珠宝的最高价值
1.题目链接
- 珠宝的最高价值
2.算法原理详解
- 思路:
-
确定状态表示 ->
dp[i][j]的含义- 到达
dp[i][j]的时候,此时的最大价值
- 到达
-
推导状态转移方程
dp[i][j] = max(dp[i - 1][j] + dp[i][j - 1]) + g[i][j]
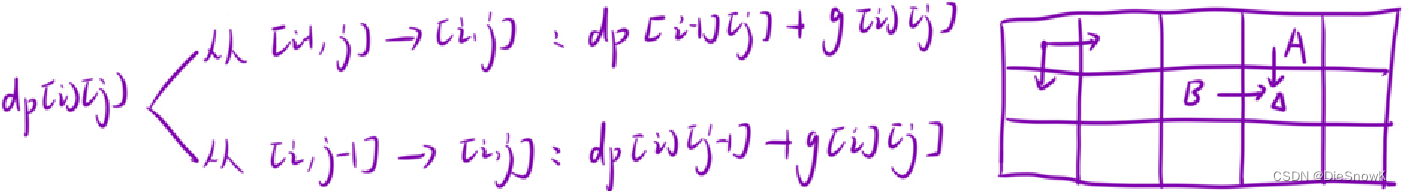
-
初始化:
dp表多开一行和一列虚拟结点,避免处理边界- 第一行和第一列全部初始化为0即可
-
确定填表顺序:从上往下,从左往右
-
确定返回值:
dp[n][m]
-
3.代码实现
int jewelleryValue(vector<vector<int>>& frame)
{
int n = frame.size(), m = frame[0].size();
vector<vector<int>> dp(n + 1, vector<int>(m + 1, 0));
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= m; j++)
{
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]) + frame[i - 1][j - 1];
}
}
return dp[n][m];
}






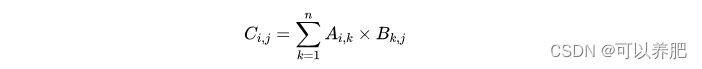

![【代码随想录】【算法训练营】【第15天】 [102]二叉树的层序遍历 [226]翻转二叉树 [101]对称二叉树](https://img-blog.csdnimg.cn/direct/1e2d24fbea6f44c98e9b74bb35aa1d24.png)

![一维前缀和[模版]](https://img-blog.csdnimg.cn/direct/7fcd78b12e1e4f4ab075ed9b9bc54c2a.png)