题目描述

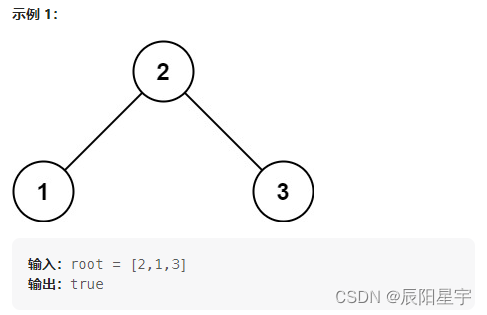
原题链接：98. 验证二叉搜索树

解题思路

BST的特点是：当前结点的值，比左子树中的全部结点都大，比右子树中全部结点都小。在代码实现中，要注意不要对比的是某一结点和某一侧的全部值之间的关系，不能只有结点与结点间的关系对比，否则容易出现非法BST。

一、递归法

根据BST的特征，

（1）中序遍历

根据BST的特点，当对BST进行中序遍历时，结点的值应呈单调递增的形式。

1）辅助vector
根据单调性，我们可以在遍历时，用vector记录结点值，然后再顺序遍历vector中的值，当以单调形式递增时，返回true，否则返回false。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> path;
    // 按中序遍历，左中右的顺序，将root中元素存入path中
    void traversal(TreeNode* root) {
        if(!root)       return ;
        traversal(root->left);
        path.push_back(root->val);
        traversal(root->right);
    }
    bool isValidBST(TreeNode* root) {
        traversal(root);
        // 若为BST，则path中元素应该单调递增
        for(int i = 0; i < path.size() - 1; i++) {
            if(path[i] >= path[i + 1])       return false;
        }
        return true;
    }
};

2）记录上一个结点的值
设置maxValue，记录上一个遍历元素的值，若为BST，则当前的值，应大于上一个遍历的值。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    // 因为测试数据中有INT_MIN和INT_MAX，所以用long long
    long long maxValue = LONG_MIN;
    bool isValidBST(TreeNode* root) {
        if(!root)       return true;
        bool left = isValidBST(root->left);
        // 中序遍历，验证元素是否从小到大递增
        if(maxValue < root->val)    maxValue = root->val;
        else            return false;
        bool right = isValidBST(root->right);
        return left && right;
    }
};

3）双指针法
为防止测试数据有LONG_MIN，因此采用记录前后元素，双指针对比数据大小的方式。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    // 设置一个指针指向前一个遍历元素
    TreeNode* pre = NULL;
    bool isValidBST(TreeNode* root) {
        if(!root)       return true;
        bool left = isValidBST(root->left);
        // 当指针不为空且指向前一个元素的值大于当前元素，则不满足单调递增
        if(pre != NULL && pre->val >= root->val)     return false;
        // 当指针为空或满足单调递增，则更新指针
        pre = root;
        bool right = isValidBST(root->right);
        return left && right;
    }
};

（2）先序遍历

BST要保证，当前节点全部大于左子树中的结点，全部小于右子树中的结点。

在向左子树遍历时，只会遇到两种情况：
（1）向左子树的左子树结点遍历；（2）向右子树的左子树结点遍历。
对于第一种情况，左子树的左子树结点，只要其左结点比当前结点小即可。对于第二种情况，不仅要求左结点要比当前结点小，还要保证不能小过之前的右子树的根结点及其以上的值。

在向右子树遍历时，同理也会遇到两种情况：
（1）向右子树的右子树结点遍历；（2）向左子树的右子树结点遍历。
对于第一种情况，右子树的右子树结点，只要其右结点比当前节点大即可。对于第二种情况，不仅要求右结点比当前结点大，还要保证不能大过之前的左子树的根结点及其以上的值。

因此，我们需要设置两个局部变量，maxleft记录当前结点的左子树不可超过的值，minright当前结点右子树中的结点不可小于的值。当遍历到左子树结点时，更新maxleft（向左应更小，因此取较小值）。当遍历到右子树结点时，更新minright（向右更大，因此取较大值）。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool res = true;
    // root：当前遍历结点、maxleft：规定左子树结点不能超过的值，minright：规定右子树中结点不能小于的值
    void traversal(TreeNode* root, long long maxleft, long long minright) {
        if(!root->left && !root->right)             return ;
        // 处理左的左和右的左
        if(root->left) {
            long long left = root->left->val;
            // 当左子树的值小于当前结点的值，若还处于右子树时，该结点的值比右子树中不能小于的值大，则继续遍历
            if(left < root->val && left > minright) {                
                // 向左子树遍历时，更新左子树结点不能超过的值，取较小值
                // long long l = root->val < maxleft ? root->val : maxleft;		
                // 这里可以不用再比较，因为当向左遍历之前成立时，说明当前结点一定小于之前的根节点
                traversal(root->left, root->val, minright);
            } else {
                res = false;
                return ;
            }            
        }
        // 处理右的右和左的右
        if(root->right) {
            long long right = root->right->val;
            // 当右子树的值大于当前结点的值，若还处于左子树时，该结点的值比左子树中不能超过的值小，则继续遍历
            if(right > root->val && right < maxleft) {
                // 向右子树遍历时，更新右子树不能小于的值，取较大值
                // long long r = root->val > minright ? root->val : minright;		
                // 这里可以不用再比较，因为当向右遍历之前成立时，说明当前结点一定大于之前的根节点
                traversal(root->right, maxleft, root->val);
            } else {
                res = false;
                return ;
            }
        }

    }
    bool isValidBST(TreeNode* root) {
        // 测试数据中有关INT_MAX和INT_MIN，因此用long long
        traversal(root, LONG_MAX, LONG_MIN);
        return res;
    }
};

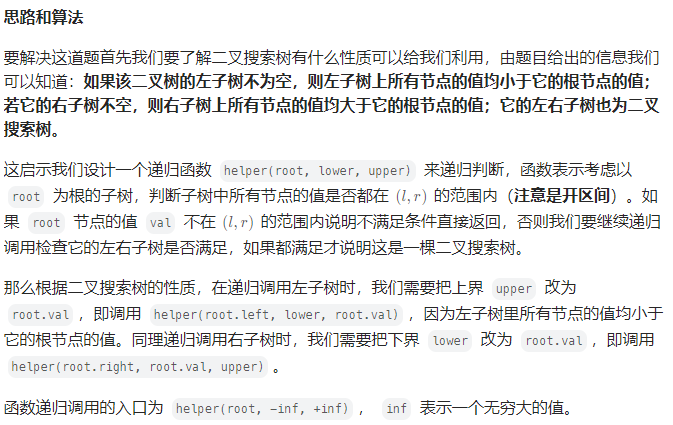
（3）后序遍历

class Solution {
public:
    bool helper(TreeNode* root, long long lower, long long upper) {
        if (root == nullptr) {
            return true;
        }
        if (root -> val <= lower || root -> val >= upper) {
            return false;
        }
        return helper(root -> left, lower, root -> val) && helper(root -> right, root -> val, upper);
    }
    bool isValidBST(TreeNode* root) {
        return helper(root, LONG_MIN, LONG_MAX);
    }
};

时间复杂度 $O(n)$
空间复杂度 $O(n)$

二、迭代法

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool isValidBST(TreeNode* root) {
        stack<TreeNode*> st;
        TreeNode* cur = root;
        TreeNode* pre = NULL;
        while(cur || !st.empty()) {
            while(cur) {
                st.push(cur);
                cur = cur->left;
            }
            cur = st.top();      st.pop();
            if(pre != NULL && cur->val <= pre-<val)
                return false;
            pre = cur;
            cur = cur->right;            
        }
    }
};

参考文章：98.验证二叉搜索树、验证二叉搜索树