代码随想录-Day17

110. 平衡二叉树

这道题中的平衡二叉树的定义是：二叉树的每个节点的左右子树的高度差的绝对值不超过 111，则二叉树是平衡二叉树。根据定义，一棵二叉树是平衡二叉树，当且仅当其所有子树也都是平衡二叉树，因此可以使用递归的方式判断二叉树是不是平衡二叉树，递归的顺序可以是自顶向下或者自底向上。

方法一：自顶向下的递归

class Solution {
    public boolean isBalanced(TreeNode root) {
        if (root == null) {
            return true;
        } else {
            return Math.abs(height(root.left) - height(root.right)) <= 1 && isBalanced(root.left) && isBalanced(root.right);
        }
    }

    public int height(TreeNode root) {
        if (root == null) {
            return 0;
        } else {
            return Math.max(height(root.left), height(root.right)) + 1;
        }
    }
}

这段代码是用来检测一棵二叉树是否是平衡二叉树的Java实现。平衡二叉树的定义是：任意两个子树的高度差不大于1。代码中定义了两个方法：isBalanced 和 height。

public boolean isBalanced(TreeNode root) 方法是主要的接口，用于判断传入的二叉树根节点 root 所代表的树是否平衡。其逻辑如下：
- 首先，如果根节点为空，直接返回 true，因为空树被认为是平衡的。
- 否则，计算左子树和右子树的高度（调用 height 方法），并取两者的高度差的绝对值。如果这个差值小于等于1，并且左子树和右子树也分别都是平衡的（递归调用 isBalanced 方法），则整棵树是平衡的，返回 true；否则，返回 false。
public int height(TreeNode root) 方法用于计算以 root 为根的二叉树的高度。其逻辑如下：
- 如果节点为空，高度为0，因为空树的高度定义为0。
- 否则，递归计算左子树和右子树的高度，并取两者中的较大值，然后加1（因为要算上根节点的高度），作为当前树的高度返回。

综上，这个解决方案通过递归计算每个子树的高度，并在回溯过程中判断树是否满足平衡的条件，最终得出整个二叉树是否平衡的结论。这种方法的时间复杂度最坏情况下是O(n^2)，因为每个节点的高度可能被重复计算多次。在实践中，对于极端不平衡的树，性能可能不是最优。有一种优化方法是将高度计算和平衡判断结合起来，只遍历树一次，但这需要更复杂的逻辑来同时跟踪和更新高度信息。

方法二：自底向上的递归

class Solution {
    public boolean isBalanced(TreeNode root) {
        return height(root) >= 0;
    }

    public int height(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int leftHeight = height(root.left);
        int rightHeight = height(root.right);
        if (leftHeight == -1 || rightHeight == -1 || Math.abs(leftHeight - rightHeight) > 1) {
            return -1;
        } else {
            return Math.max(leftHeight, rightHeight) + 1;
        }
    }
}

这段代码同样是用于判断一棵二叉树是否是平衡二叉树的问题，但是实现方式稍有不同，主要是优化了递归过程中的剪枝逻辑。下面是代码的解析：

public boolean isBalanced(TreeNode root) 方法仍然是主接口，用于判断二叉树是否平衡，但它直接依赖于 height 方法的返回值。如果 height(root) 返回值大于等于0，则表示树是平衡的，因为只有在树不平衡的情况下 height 方法才会返回-1。
public int height(TreeNode root) 方法用于计算以 root 为根的子树的高度，同时在此过程中判断这棵子树是否平衡。其逻辑如下：
- 基准情况：如果节点为空，返回高度为0，表示空树是平衡的。
- 递归计算左子树和右子树的高度，分别赋值给 leftHeight 和 rightHeight。
- 在这里进行了关键的平衡性检查：如果 leftHeight 或 rightHeight 为-1，表示之前已经判断出对应的子树不平衡；或者 leftHeight 和 rightHeight 之差的绝对值大于1，也说明当前子树不平衡。在这两种不平衡的情况下，直接返回-1，这样在上一层递归调用中就能立刻知道当前路径下的树是不平衡的，无需继续深入计算其它分支，达到剪枝效果，提高效率。
- 如果上述条件都不满足，即当前子树是平衡的，那么返回左右子树最大高度加1作为当前子树的高度。

这种实现方式巧妙地将平衡性检查与高度计算结合在一起，通过返回-1作为不平衡的标志，能够在递归过程中尽早终止不必要的计算，是一种较为高效的解法。时间复杂度为O(n)，在最好的情况下（完全平衡的树）也能保持较好的效率。

257. 二叉树的所有路径

给你一个二叉树的根节点 root ，按任意顺序，返回所有从根节点到叶子节点的路径。
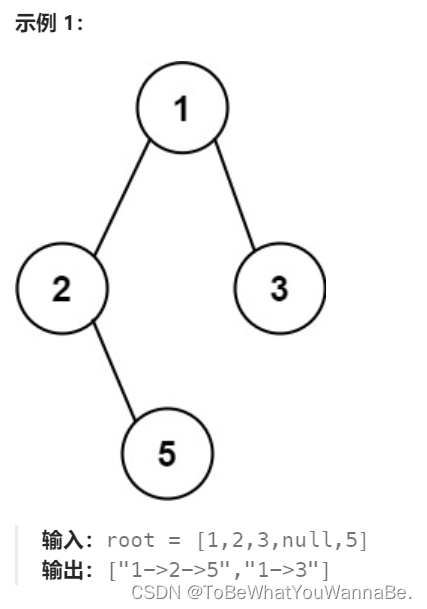
在这里插入图片描述

方法一：深度优先搜索

class Solution {
    public List<String> binaryTreePaths(TreeNode root) {
        List<String> paths = new ArrayList<String>();
        constructPaths(root, "", paths);
        return paths;
    }

    public void constructPaths(TreeNode root, String path, List<String> paths) {
        if (root != null) {
            StringBuffer pathSB = new StringBuffer(path);
            pathSB.append(Integer.toString(root.val));
            if (root.left == null && root.right == null) {  // 当前节点是叶子节点
                paths.add(pathSB.toString());  // 把路径加入到答案中
            } else {
                pathSB.append("->");  // 当前节点不是叶子节点，继续递归遍历
                constructPaths(root.left, pathSB.toString(), paths);
                constructPaths(root.right, pathSB.toString(), paths);
            }
        }
    }
}

这段代码是用来解决一个经典的二叉树问题：找出一颗二叉树中所有从根节点到叶子节点的路径，并以字符串形式返回这些路径。每条路径以节点值的序列表示，并且序列中相邻节点值之间由 “->” 连接。代码中定义了两个方法：binaryTreePaths 和 constructPaths。

public List<String> binaryTreePaths(TreeNode root) 是主要的接口，接收一个 TreeNode 类型的参数 root 表示二叉树的根节点，返回值是一个字符串列表，包含所有从根到叶子的路径。首先初始化一个 List<String> 类型的 paths 用于存储所有路径，然后调用 constructPaths 函数递归构建路径，最后返回 paths。
public void constructPaths(TreeNode root, String path, List<String> paths) 是递归辅助函数，用于构造从当前节点 root 到叶子节点的所有路径，并将这些路径添加到 paths 中。
- 如果当前节点 root 不为空，首先将当前节点的值转换成字符串追加到路径 path 上，这里使用 StringBuffer 来避免频繁创建新的字符串对象，提高效率。
- 接下来，检查当前节点是否为叶子节点（即没有左右子节点）。如果是叶子节点，将当前的路径加入到结果列表 paths 中。
- 如果当前节点不是叶子节点，说明还需要继续遍历其左右子树。在递归调用前，向路径中添加一个 “->” 符号，表示路径的延续，然后分别对左子树和右子树进行递归调用，传递更新后的路径字符串。

最终，binaryTreePaths 函数会返回包含所有从根到叶子节点路径的字符串列表。这种方法有效地遍历了二叉树的所有路径，且由于使用了递归，代码较为简洁明了。

方法二：广度优先搜索

class Solution {
    public List<String> binaryTreePaths(TreeNode root) {
        List<String> paths = new ArrayList<String>();
        if (root == null) {
            return paths;
        }
        Queue<TreeNode> nodeQueue = new LinkedList<TreeNode>();
        Queue<String> pathQueue = new LinkedList<String>();

        nodeQueue.offer(root);
        pathQueue.offer(Integer.toString(root.val));

        while (!nodeQueue.isEmpty()) {
            TreeNode node = nodeQueue.poll(); 
            String path = pathQueue.poll();

            if (node.left == null && node.right == null) {
                paths.add(path);
            } else {
                if (node.left != null) {
                    nodeQueue.offer(node.left);
                    pathQueue.offer(new StringBuffer(path).append("->").append(node.left.val).toString());
                }

                if (node.right != null) {
                    nodeQueue.offer(node.right);
                    pathQueue.offer(new StringBuffer(path).append("->").append(node.right.val).toString());
                }
            }
        }
        return paths;
    }
}

这段代码是另一种实现方式，用来找出一棵二叉树中所有从根节点到叶子节点的路径，并以字符串形式返回这些路径。与之前的递归解法不同，这里采用广度优先搜索（BFS）的方式遍历二叉树。代码中定义了两个队列：一个用于存储待访问的节点，另一个用于存储到达每个节点时的路径字符串。

public List<String> binaryTreePaths(TreeNode root) 方法是主要接口，接收一个 TreeNode 类型的参数 root 作为二叉树的根节点，返回值是一个字符串列表，包含所有从根到叶子的路径。首先初始化一个空的 List<String> paths 用于收集所有路径。如果根节点为空，直接返回空列表。然后，创建两个队列 nodeQueue 和 pathQueue 分别用于存放节点和对应的路径字符串，将根节点及其值的字符串形式入队。
使用 while 循环处理队列直到 nodeQueue 为空，每次循环：
- 出队一个节点 node 和对应的路径字符串 path。
- 如果当前节点 node 是叶子节点（即没有左右子节点），则将当前路径加入到结果列表 paths 中。
- 如果当前节点有子节点，依次将左子节点和右子节点（如果存在）入队，并构造它们的新路径字符串（基于当前路径加上 “->” 和节点值），然后也将新路径入队 pathQueue。
循环结束后，paths 列表中包含了所有从根到叶子的路径，直接返回即可。

这种方法利用了广度优先搜索的特性，逐层遍历树的节点，使用队列维护待处理的节点和路径，能够有效地遍历整棵树并收集所有路径，同时避免了递归可能导致的栈溢出问题。

404. 左叶子之和

给定二叉树的根节点 root ，返回所有左叶子之和。
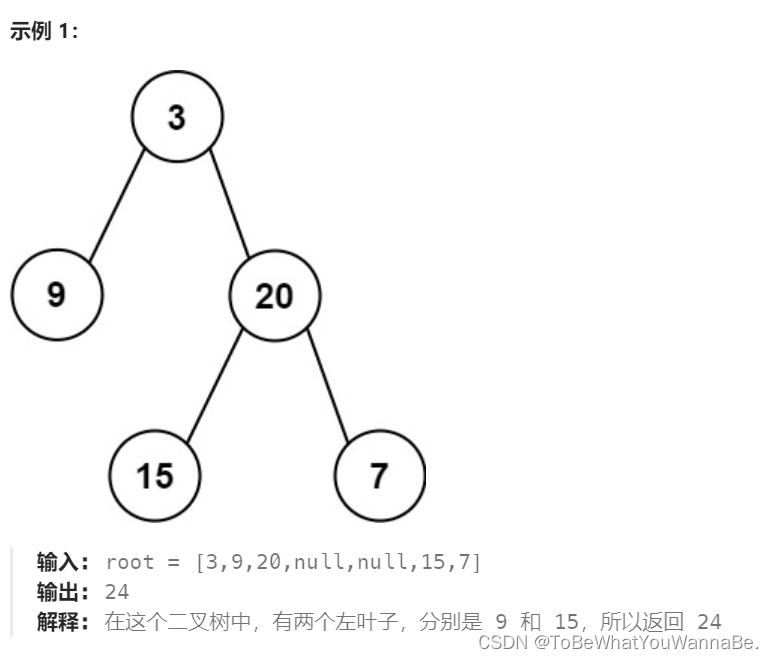
在这里插入图片描述

方法一：深度优先搜索

class Solution {
    public int sumOfLeftLeaves(TreeNode root) {
        return root != null ? dfs(root) : 0;
    }

    public int dfs(TreeNode node) {
        int ans = 0;
        if (node.left != null) {
            ans += isLeafNode(node.left) ? node.left.val : dfs(node.left);
        }
        if (node.right != null && !isLeafNode(node.right)) {
            ans += dfs(node.right);
        }
        return ans;
    }

    public boolean isLeafNode(TreeNode node) {
        return node.left == null && node.right == null;
    }
}

这段代码是用来求解一个二叉树问题的，具体是计算给定二叉树中所有左叶子节点之和。代码定义了三个方法：sumOfLeftLeaves、dfs 和 isLeafNode。

public int sumOfLeftLeaves(TreeNode root) 是主方法，接收一个 TreeNode 类型的参数 root 作为二叉树的根节点，返回值是所有左叶子节点的值之和。如果根节点为空，直接返回0。否则，调用深度优先搜索（DFS）方法 dfs 并传入根节点，返回其结果。
public int dfs(TreeNode node) 是深度优先搜索的实现，用于递归地遍历二叉树。对于当前节点 node：
- 首先初始化答案变量 ans 为0。
- 如果当前节点的左子节点不为空，判断这个左子节点是否为叶子节点（调用 isLeafNode 方法）。如果是，直接将该左叶子节点的值累加到 ans；如果不是叶子节点，则递归调用 dfs 并累加返回值。
- 接着，如果当前节点的右子节点不为空且不是叶子节点，递归调用 dfs 并累加右子树的返回值。注意这里只对非叶子的右子节点进行递归，因为题目要求的是左叶子节点之和，右子节点仅在它不是叶子节点时才可能贡献额外的和（通过其自身的左叶子节点）。
- 最后返回 ans，即经过当前节点后累加的左叶子节点之和。
public boolean isLeafNode(TreeNode node) 是一个辅助方法，用于判断给定的节点是否为叶子节点（即没有左右子节点），返回布尔值。

通过这样的递归遍历，代码能高效地计算出二叉树中所有左叶子节点的值之和。

方法二：广度优先搜索

class Solution {
    public int sumOfLeftLeaves(TreeNode root) {
        if (root == null) {
            return 0;
        }

        Queue<TreeNode> queue = new LinkedList<TreeNode>();
        queue.offer(root);
        int ans = 0;
        while (!queue.isEmpty()) {
            TreeNode node = queue.poll();
            if (node.left != null) {
                if (isLeafNode(node.left)) {
                    ans += node.left.val;
                } else {
                    queue.offer(node.left);
                }
            }
            if (node.right != null) {
                if (!isLeafNode(node.right)) {
                    queue.offer(node.right);
                }
            }
        }
        return ans;
    }

    public boolean isLeafNode(TreeNode node) {
        return node.left == null && node.right == null;
    }
}

这段代码提供了另一种解决方案，使用广度优先搜索（BFS）的方法来计算给定二叉树中所有左叶子节点的值之和。与之前的深度优先搜索（DFS）版本相比，这里使用了队列来进行层次遍历。代码中定义了两个方法：sumOfLeftLeaves 和 isLeafNode。

public int sumOfLeftLeaves(TreeNode root) 是主方法，接收一个 TreeNode 类型的参数 root 作为二叉树的根节点，返回值是所有左叶子节点的值之和。如果根节点为空，直接返回0。初始化一个队列 queue，并将根节点放入队列。定义一个变量 ans 用于累计左叶子节点的值。然后进入一个循环处理队列直到其为空。
- 在循环中，每次从队列中取出一个节点 node。
- 检查 node 的左子节点是否存在，如果存在并且是叶子节点（调用 isLeafNode 判断），则将左叶子节点的值累加到 ans；如果左子节点不是叶子节点，则将它加入队列以便后续遍历。
- 接着检查 node 的右子节点，如果右子节点存在且不是叶子节点，则将其加入队列。这里右子节点的叶子状态不影响累加和，但可能包含其他左叶子节点，故需继续遍历。
循环结束后，返回累计的左叶子节点值之和 ans。
public boolean isLeafNode(TreeNode node) 是一个辅助方法，用于判断给定的节点是否为叶子节点，即没有左右子节点，返回布尔值。