本文使用机器学习SVM对数据进行预测。仅供参考
1、数据
1.1 训练数据集:
medol.xlsx文件示例
| o | t | v |
| 30 | 15 | -1.915362209 |
| 30 | 18 | -1.963409776 |
| 30 | 21 | -1.762028408 |
| 30 | 24 | -1.789477583 |
1.2 预测数据集
test.xlsx文件示例
| o | t |
| 35 | 16 |
| 35 | 19 |
2、模型训练
train.py
import pandas as pd
from sklearn.svm import SVR
from sklearn.model_selection import GridSearchCV, train_test_split
from sklearn.metrics import mean_absolute_error, mean_squared_error, r2_score
from sklearn.preprocessing import StandardScaler
import joblib
import numpy as np
import matplotlib.pyplot as plt
# 加载数据
df = pd.read_excel("model.xlsx")
# 定义特征列
feature_columns = ['o', 't']
# 初始化标准化器
scaler = StandardScaler()
# 归一化数据集
X_scaled = scaler.fit_transform(df[feature_columns])
target_column = 'v'
# 将数据拆分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X_scaled, df[target_column], test_size=0.1)
# 初始化SVM回归器
svm = SVR()
# 定义参数网格
param_grid = {
'kernel': ['linear', 'rbf'],
'C': [1, 10, 100],
'gamma': [0.1, 1, 10],
}
# 使用GridSearchCV进行网格搜索
grid_search = GridSearchCV(svm, param_grid, cv=5, scoring='neg_mean_squared_error', verbose=1)
grid_search.fit(X_train, y_train)
# 获取最佳模型
best_model_svm = grid_search.best_estimator_
# 输出最佳超参数
print("最佳超参数 for SVM:", grid_search.best_params_)
# 计算训练集和测试集的指标
train_predictions_svm = best_model_svm.predict(X_train)
test_predictions_svm = best_model_svm.predict(X_test)
# 训练集指标
print("\n[训练集指标 - SVM]")
print("平均绝对误差: {}".format(mean_absolute_error(y_train, train_predictions_svm)))
print("均方误差: {}".format(mean_squared_error(y_train, train_predictions_svm)))
print("均方根误差: {}".format(np.sqrt(mean_squared_error(y_train, train_predictions_svm))))
print("R2分数: {}".format(r2_score(y_train, train_predictions_svm)))
# 测试集指标
print("\n[测试集指标 - SVM]")
print("平均绝对误差: {}".format(mean_absolute_error(y_test, test_predictions_svm)))
print("均方误差: {}".format(mean_squared_error(y_test, test_predictions_svm)))
print("均方根误差: {}".format(np.sqrt(mean_squared_error(y_test, test_predictions_svm))))
print("R2分数: {}".format(r2_score(y_test, test_predictions_svm)))
# 绘制训练集误差随循环次数的变化图
plt.plot(range(1, len(best_model_svm.support_vectors_) + 1), best_model_svm.dual_coef_.ravel(), label='Train Error')
plt.xlabel('Support Vectors')
plt.ylabel('Dual Coefficients')
plt.title('Training Set Error Over Support Vectors')
plt.legend()
plt.show()
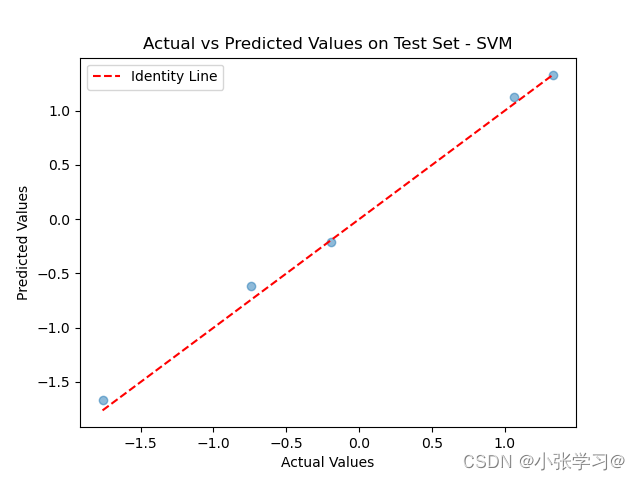
# 绘制测试集的实际值和预测值的对比图
plt.scatter(y_test, test_predictions_svm, alpha=0.5)
plt.plot([min(y_test), max(y_test)], [min(y_test), max(y_test)], '--', color='red', label='Identity Line')
plt.xlabel('Actual Values')
plt.ylabel('Predicted Values')
plt.title('Actual vs Predicted Values on Test Set - SVM')
plt.legend()
plt.show()
# 保存训练好的SVM模型
svm_model_filename = 'svm_model'
joblib.dump(best_model_svm, svm_model_filename)
# 保存训练好的标准化器
joblib.dump(scaler, 'scaler_model_svm')
3、预测模型
test.py
import pandas as pd
import joblib
from sklearn.preprocessing import StandardScaler
# 加载训练好的模型并在新数据上进行预测 (test.xlsx)
test_df = pd.read_excel("test.xlsx")
# 初始化 StandardScaler
scaler = joblib.load('scaler_model')
predicted_columns = []
model_filename = f'svm_model'
# 加载模型
loaded_model = joblib.load(model_filename)
# 在新数据上进行预测
predictions = loaded_model.predict(scaler.transform(test_df[['o', 't']]))
# 将预测结果存储在列表中
predicted_columns.append(predictions)
# 使用 pd.concat(axis=1) 将所有列一次性连接到 DataFrame 中
predicted_df = pd.concat([test_df] + [pd.Series(predictions, name=f'v') for i, predictions in enumerate(predicted_columns, start=1)], axis=1)
# 保存更新后的 test_df
predicted_df.to_excel("predicted.xlsx", index=False)4、结果
最佳超参数 for SVM: {'C': 1, 'gamma': 0.1, 'kernel': 'linear'}
[训练集指标 - SVM]
平均绝对误差: 0.09572890288084648
均方误差: 0.01428879779657209
均方根误差: 0.11953575948883284
R2分数: 0.9939848933501038
[测试集指标 - SVM]
平均绝对误差: 0.06024996260030221
均方误差: 0.00572260737850485
均方根误差: 0.07564791721194213
R2分数: 0.9956600567712165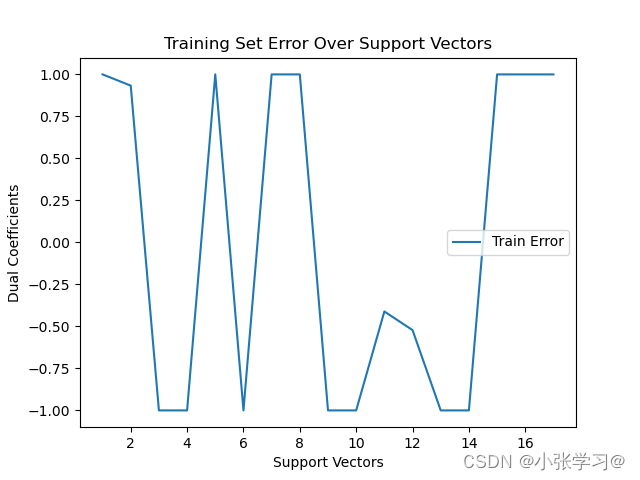
若有问题,欢迎讨论