目录

堆的性质：

堆的实现

堆向下调整算法

堆的创建

堆的插入

堆的删除

堆的应用

堆排序

对比冒泡的优势：

代码

头文件

源文件

---

如果有一个关键码的集合K = { ， ， ，…， }，把它的所有元素按完全二叉树的顺序存储方式存储 在一个一维数组中，并满足： 且 = 且 >= ) i = 0，1， 2…，则称为小堆(或大堆)。将根结点最大的堆叫做最大堆或大根堆，根结点最小的堆叫做最小堆或小根堆。

堆的性质：

堆中某个结点的值总是不大于或不小于其父结点的值； 堆总是一棵完全二叉树。

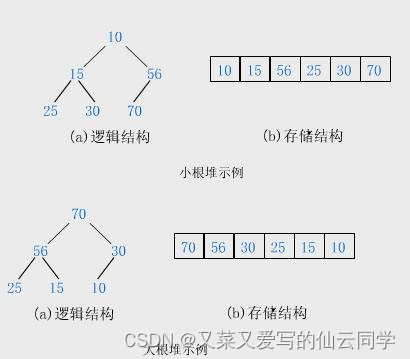
堆的实现

堆向下调整算法

现在我们给出一个数组，逻辑上看做一颗完全二叉树。我们通过从根结点开始的向下调整算法可以把它调整 成一个小堆。向下调整算法有一个前提：左右子树必须是一个堆，才能调整。

int array[] = {27,15,19,18,28,34,65,49,25,37};

堆的创建

下面我们给出一个数组，这个数组逻辑上可以看做一颗完全二叉树，但是还不是一个堆，现在我们通过算 法，把它构建成一个堆。根结点左右子树不是堆，我们怎么调整呢？这里我们从倒数的第一个非叶子结点的 子树开始调整，一直调整到根结点的树，就可以调整成堆。

int a[] = {1,5,3,8,7,6};

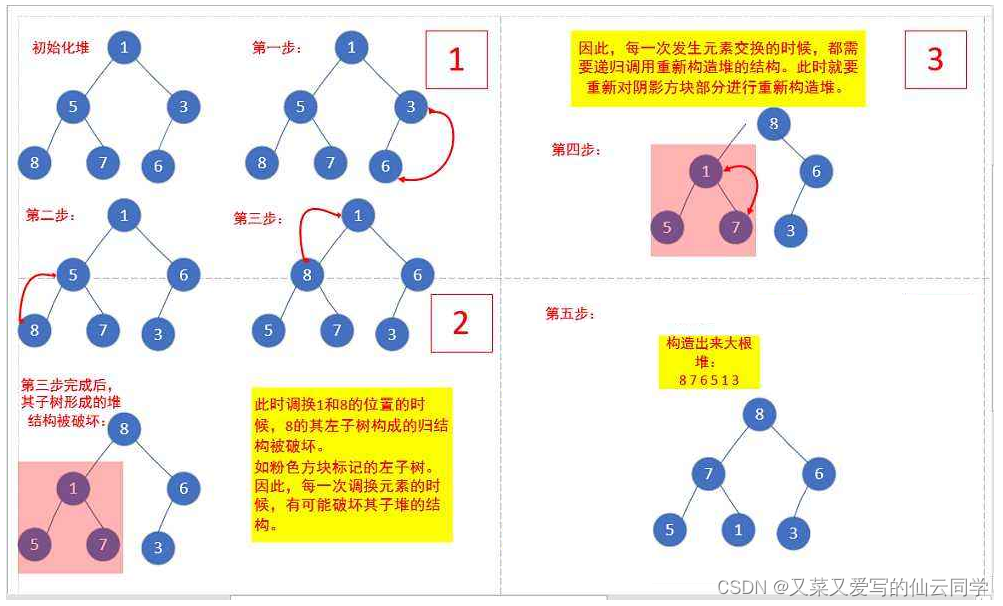
堆的插入

先插入一个10到数组的尾上，再进行向上调整算法，直到满足堆。

堆的删除

删除堆是删除堆顶的数据，将堆顶的数据根最后一个数据一换，然后删除数组最后一个数据，再进行向下调 整算法。

堆的应用

堆排序

堆排序即利用堆的思想来进行排序，总共分为两个步骤：

1. 建堆

升序：建大堆

降序：建小堆

2. 利用堆删除思想来进行排序

建堆和堆删除中都用到了向下调整，因此掌握了向下调整，就可以完成堆排序。

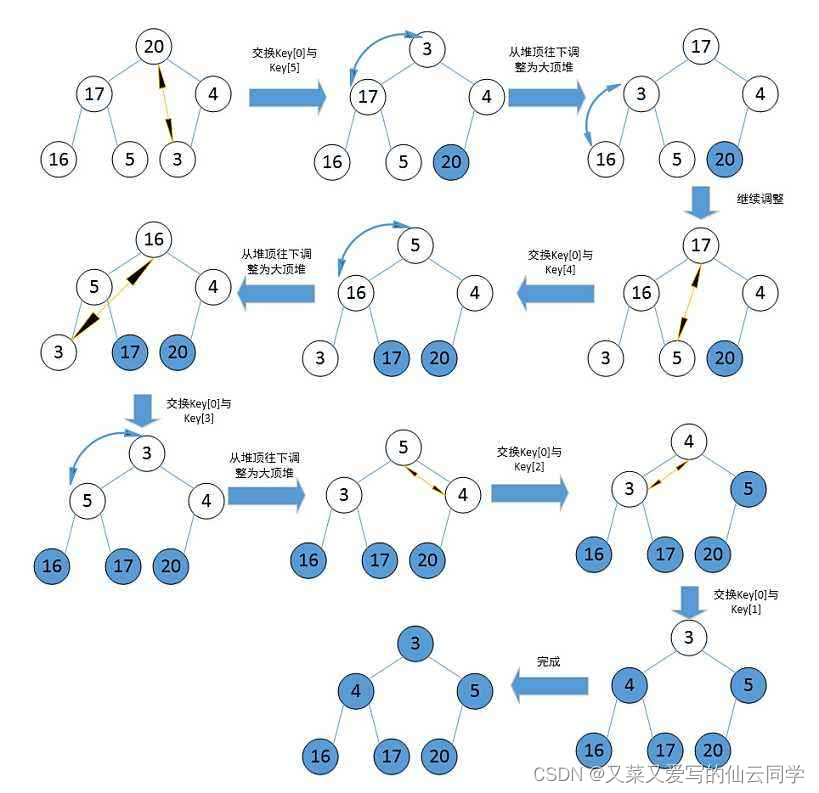
对比冒泡的优势：

堆排序时间复杂度为nlogn

而冒泡则为n^2，效率大大提高

代码

头文件

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
typedef int HPDataType;    //大根堆
typedef struct Heap
{
	HPDataType* _a;
	int _size;
	int _capacity;
}Heap;

void HeapInit(Heap* php);
// 堆的销毁
void HeapDestory(Heap* hp);
// 堆的插入
void HeapPush(Heap* hp, HPDataType x);
// 堆的删除
void HeapPop(Heap* hp);
// 取堆顶的数据
HPDataType HeapTop(Heap* hp);
// 堆的数据个数
int HeapSize(Heap* hp);
// 堆的判空
int HeapEmpty(Heap* hp);
//堆排序1(向上与向下堆)
void HeapSort1(int* a, int n);
//堆排序2(纯向下)
void HeapSort2(int* a, int n);

源文件

#define _CRT_SECURE_NO_WARNINGS 1
#include"heap.h"
void HeapInit(Heap* php) {
	assert(php);
	php->_a = NULL;
	php->_capacity = php->_size = 0;
}
void extendcapacity(Heap* php){
	assert(php);
	HPDataType* mn;
	if (php->_capacity == 0) {
		mn = (HPDataType*)malloc(sizeof(HPDataType) * 4);
		php->_capacity = 4;
		php->_a = mn;
		return;
	}
	else {
		mn = (HPDataType*)realloc(php->_a,sizeof(HPDataType) * (2*php->_capacity));
		php->_capacity *= 2;
		php->_a = mn;
		return;
	}
}
void HeapDestory(Heap* hp) {
	free(hp->_a);
	hp->_a = NULL;
	hp->_capacity = hp->_size = 0;
}
void swap(HPDataType* a, HPDataType* b) {
	int tmp;
	tmp = *a;
	*a = *b;
	*b = tmp;
}
void adjustup(HPDataType* x, HPDataType now) {
	int parent = (now - 1) / 2, child = now;
	while (child > 0) {
		if (x[child] > x[parent]) {
			swap(&x[child], &x[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
			break;
	}
}
void HeapPush(Heap* hp, HPDataType x) {
	assert(hp);
	if (hp->_capacity == hp->_size)
		extendcapacity(hp);
	hp->_a[hp->_size] = x;
	adjustup(hp->_a,hp->_size);
	hp->_size++;
}
void adjustdown(HPDataType* x, HPDataType size) {
	int parent=0, child=1;
	while (child < size) {
		if (x[parent * 2 + 2] > x[child])
			child = parent * 2 + 2;
		if (x[child] > x[parent]) {
			swap(&x[child], &x[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
			break;
	}
}
void HeapPop(Heap* hp) {
	assert(hp);
	hp->_a[0] = hp->_a[hp->_size - 1];
	hp->_size--;
	adjustdown(hp->_a, hp->_size);
}
HPDataType HeapTop(Heap* hp) {
	return hp->_a[0];
}
int HeapSize(Heap* hp) {
	return hp->_size;
}
int HeapEmpty(Heap* hp) {
	return hp->_size == 0;
}
void HeapSort1(int* a, int n) {     //由下往上使用向上堆
	int i;
	for (i = 1; i < n; i++)
		adjustup(a, i);
	for (i = n - 1; i > 0; i--) {
		swap(&a[0], &a[i]);
		adjustdown(a, i-1);
	}
}
void HeapSort2(int* a, int n) {    //由最后一个父节点往上使用向下堆
	int i;
	for (i =(n-2)/2; i > 1; i--)
		adjustdown(a, i);
	for (i = n - 1; i > 0; i--) {
		swap(&a[0], &a[i]);
		adjustdown(a, i - 1);
	}
}