前言
这个也是对《数学模型》(姜启源第四版)书内容的摘抄
建立数学模型
数学模型这个词汇现在越来越多地出现在现代入的 生产、工作和社会活动中.广大的科学技 术人员和应用数学工作者来说,建立数学模型是沟通摆在面前的实际问题与他 们掌握的数学工具之间联系的一座必不可少的桥梁.本章主要讨论建立数学模型的意义、方法和步骤,以及建立数学模型的全面的、初步的了解。
从现实对象到数学模型
原型和模型
原型和模型是一对对偶体
原型指人们在现实世界里关心、研究或者从事生产、管理的实际对象
模型则指为了某个特定目的将原型的某一部分信息简缩、提炼而构造的原型替代物
构造模型的目的性,模型不是原型原封不动的复制品,原型有各个方面和各种层次的特征,而模型只要求反映与某种目的有关的那些方面和层次.毫不涉及实体.所以模型的基本特征是由构造模型的目的决定的.
模型分类
按照模型替代原型的方式来分类:模型可以分为物质模型(形象模型)和理想模型(抽象模型).
前者包括直观模型、物理模型等,后者包括思维模型、符号模型、数学模型等
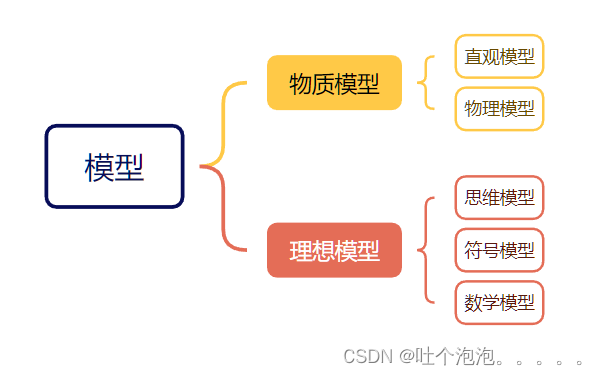
直观模型
指那些供展览用的实物模型,以及玩具、照片等,通常是把原型的尺寸按比例缩小或放大,主要追求外观上的逼真,这类模型的效果是一目了然的.
物理模型
主要指科技工作者为了一定目的根据相似原理构造的模型,
它不仅可以显示原型的外形或某些特征,而且可以用来进行模拟实验,间接地研究原型的某些规律.
物理模型常可得到实用上很有价值的结果,但也存在成本高、时间长、不灵活等缺点.
思维模型
指通过人们对原型的反复认识,将获取的知识以经验形式直接贮存于人脑中,从而可以根据思维或直觉作出相应的决策.
思维模型便于接受,也可以在一定条件下获得满意的结果,但是它往往带有模糊性、片面性、主观性、偶然性等缺点,难以对它的假设条件进行检验,并且不便于人们的相互沟通.
符号模型
是在一些约定或假设下借助于专门的符号、线条等,按一定形式组合起来描述原型,如地图、电路图、化学结构式等,具有简明、方便、目的性强及非最化等特点.
数学模型(重点)
本书要专门讨论的数学模型则是由数字、字母或其他数学符号组成的,描述现实对象数量规律的数学公式、图形或算法.
如“航行问题”:
甲乙两地相距750 km,船从甲到乙顺水航行需30h,从乙到甲逆水航行需50 h,问船速、水速各若干?
用x,y分别代表船速和水速,
可以列出方程
(x+y)·30=750,
(x-y)·50=750
实际上,这组方程就是上述航行问题的数学模型.
列出方程,原问题已转化为纯粹的数学问题.
方程的解x=20km/h,y=5km/h,
最终给出了航行问题的答案·
真正实际问题的数学模型通常要复杂得多,但是建立数学模型的基本内容已经包含在解这个代数应用题的过程中了
那就是:
1.根据建立数学模型的目的和问题的背景作出必要的简化假设(航行中设船速和水速为常数);
2.用字母表示待求的未知量(x,y代表船速和水速);
3.利用相应的物理或其他规律(匀速运动的距离等于速度乘以时间),列出数学式子(二元一次方程):
4.求出数学上的解答(z=20,y=5);
5.用这个答案解释原问题(船速和水速分别为20km/h 和km/h);
6.最后还要用实际现象来验证上述结果.
数学模型可以描述为——对于现实世界的一个特定对象,为了一个特定目的,根据特有的内在规律,作出一些必要的简化假设,运用适当的数学工具,得到的一个数学结构.
与数学模型有密切关系的数学模拟,主要指运用数字式计算机的计算机模拟.它根据实际系统或过程的特性,按照一定的数学规律用计算机程序语言模拟实际运行状况,并依据大量模拟结果对系统或过程进行定量分析.
例如通过各种工件在不同机器上按一定工艺顺序加工的模拟,能够识别生产过程中的瓶颈环节;
通过高速公路上交通流的模拟,可以分析车辆在路段上的分布特别是堵塞的状况.
与用物理模型的模拟实验相比,计算机模拟有明显的优点:成本低、时间短、重复性高、灵活性强。
数学建模的重要意义
分析与设计
例如描述药物浓度在人体内的变化规律以分析药物的疗效;建立跨音速流和激波的数学模型,用数值模拟设计新的飞机翼型.
预报与决策
生产过程中产品质量指标的预报、气象预报、人口预报、经济增长预报等等,都要有预报模型;使经济效益最大的价格策略、使费用最少的设备维修方案,都是决策模型的例子.
控制与优化
电力、化工生产过程的最优控制、零件设计中的参数优化,要以数学模型为前提,建立大系统控制与优化的数学模型,是迫切需要和十分棘手的课题.
规划与管理
生产计划、资源配置、运输网络规划、水库优化调度,以及排队策略、物资管理等,都可以用数学规划模型解决.
数学建模与计算机技术的关系密不可分.
数学建模的基本方法和步骤
数学建模面临的实际问题是多种多样的,建模的目的不同、分析的方法不同、采用的数学工具不同,所得模型的类型也不同,我们不能指望归纳出若干条准则,适用于一切实际问题的数学建模方法,下面所谓基本方法不是针对具体问题而是从方法论的意义上讲的.
数学建模的基本方法
一般说来,建模方法大体上可分为机理分析和测试分析两种,
机理分析是根据对客观事物特性的认识,找出反映内部机理的数量规律,建立的模型常有明确的物理或现实意义.
测试分析是将研究对象看作一个“黑箱”系统(意思是它的内部机理看不清楚),通过对系统输入、输出数据的测量和统计分析,按照一定的准则找出与数据拟合得最好的模型.
哪一种方法建模,主要取决于人们对研究对象的了解程度和建模目的
如果掌握了一些内部机理的知识,模型也要求具有反映内在特征的物理意义,建模就应以机理分析为主.
而如果对象的内部规律基本上不清楚,模型也不需要反映内部特性(例如仅用于对输出作预报),那么就可以用测试分析.
对于许多实际问题还常常将两种方法结合起来建模,即用机理分析建立模型的结构,用测试分析确定模型的参数.
机理分析当然要针对具体问题来做,不可能有统一的方法,因而主要是通过实例研究(Case Studies)来学习
测试分析有一套完整的数学方法,统计回归模型是其中的一小部分,以动态系统为主的测试分析称为系统辨识。
以后所说的数学建模主要指机理分析
数学建模一般步骤
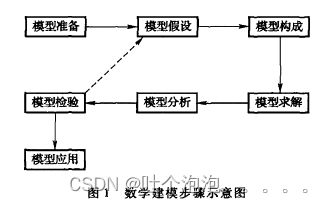
模型准备
了解问题的实际背景,明确建模目的,搜集必要的信息如现象、数据等,尽量弄清对象的主要特征,形成一个比较清晰的“问题”,由此初步确定用哪一类模型.情况明才能方法对.在模型准备阶段要深入调查研究,虚心向实际工作者请教,尽量掌握第一手资料.
模型假设
根据对象的特征和建模目的,抓住问题的本质,忽略次要因素作出必要的、合理的简化假设,对于建模的成败这是非常重要和困难的一步.
假设作得不合理或太简单,会导致错误的或无用的模型;
假设作得过分详细,试图把复杂对象的众多因素都考虑进去,会使你很难或无法继续下一步的工作.
常常要在合理与简化之间作出恰当的折中,通常,
作假设的依据,
一是出于对问题内在规律的认识,
二是来自对现象、数据的分析,
二者的综合.想象力、洞察力、判断力以及经验,在模型假设中起着重要作用.
模型构成
根据所作的偎设,用数学的语言、符号描述对象的内在规律,建立包含常量、变量等的数学模型,如优化模型、微分方程模型、差分方程模型、图的模型等.
注意使用类比法,分析对象与熟悉的其他对象的共性,借用已有的模型,建模时还应遵循的一个原则是:尽量采用简单的数学工具因为你的模型总是希望更多的人了解和使用,而不是只供少数专家欣赏.
模型求解
可以采用解方程、画图形、优化方法、数值计算、统计分析等各种数学方法,特别是数学软件和计算机技术.
模型分析
对求解结果进行数学上的分析,如结果的误差分析、统计分析模型对数据的灵敏性分析、对假设的强健性分析等.
模型检验
把求解和分析结果翻译回到实际问题,与实际的现象、数据比较,检验模型的合理性和适用性.
如果结果与实际不符,问题常常出在模型假设上,应该修改、补充假设,重新建模,这一步对于模型是否真的有用非常关键,要以严肃认真的态度对待,有些模型要经过几次反复,不断完善,直到检验结果获得某种程度上的满意.
模型应用
应用的方式与问题性质、建模目的及最终的结果有关,一般不属于本书讨论的范围.
应当指出,并不是所有问题的建模都要经过这些步,有时各步之间的界限也不那么分明,建模时不要拘泥于形式上的按部就班,本书的实例就采用了灵活的表述形式.
数学建模的全过程
从前面几个建模示例以及一般步骤的分析,可以将数学建模的过程分为表述、求解、解释、验证几个阶段,并且通过这些阶段完成从现实对象到数学模型再从数学模型回到现实对象的循环,如图2所示.
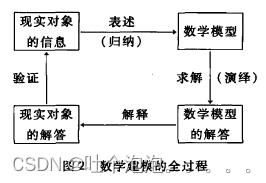
表述是将现实问题“翻译”成抽象的数学问题,属于归纳法.数学模型的求解则属于演绎法.归纳是依据个别现象推出一般规律.