文章目录
- 一、什么是雷达成像
- (1)主要的遥感探测手段:光学、红外和雷达
- (2)从数学的角度:雷达成像主要研究什么?
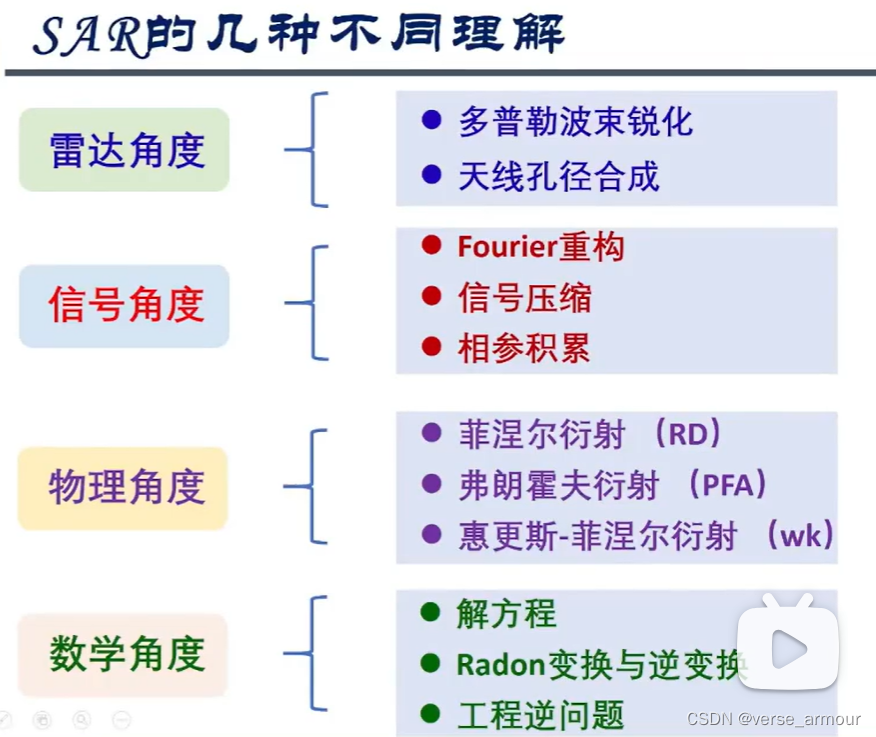
- 二、SAR的多维理解
- (1)雷达角度理解SAR
- (2)信号处理角度理解SAR
- 为什么可以从回波信号变换到两维频谱?为什么说回波信号就反映了频谱?——数学原理
- (3)数学角度理解SAR
- 离散情况
- 离散情况重构图像:反投影算法
- 连续情况
- 连续情况重构图像:Randon变换和反变换
- 三、SAR成像算法的统一解释
- (1)极坐标格式算法
- 极坐标格式转换
- (2)距离徙动算法
- (3)卷积反投影算法
https://www.bilibili.com/video/BV1fG4y1y7Eq/?spm_id_from=333.788&vd_source=e3f5663396069f720fed59c6d41ed6f7
一、什么是雷达成像
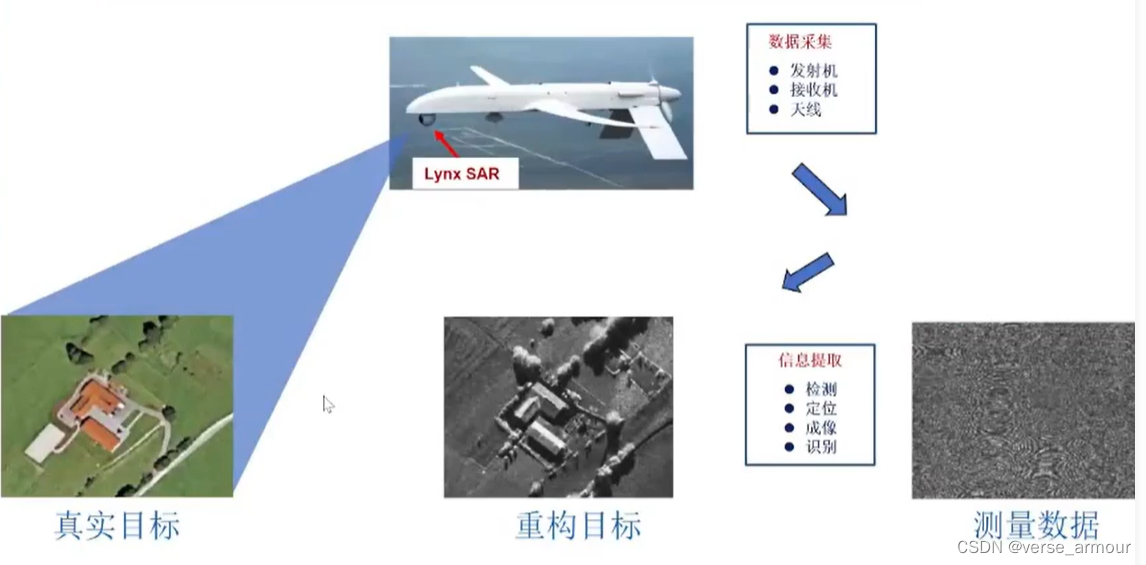
成像雷达是一种主动传感器,它利用电磁波作为媒介,采集目标回拨数据,并从回波数据中提取目标空间集合形状信息(重构目标图像)
(1)主要的遥感探测手段:光学、红外和雷达
雷达成像相比于光学成像、红外成像的优势:
- 全天候工作(不受气候条件限制)
- 全天时工作(不受白天黑夜限制)
- 探测距离远(几百公里甚至几千公里)
- 是光学、红外的补充(不同频谱观察)
(2)从数学的角度:雷达成像主要研究什么?
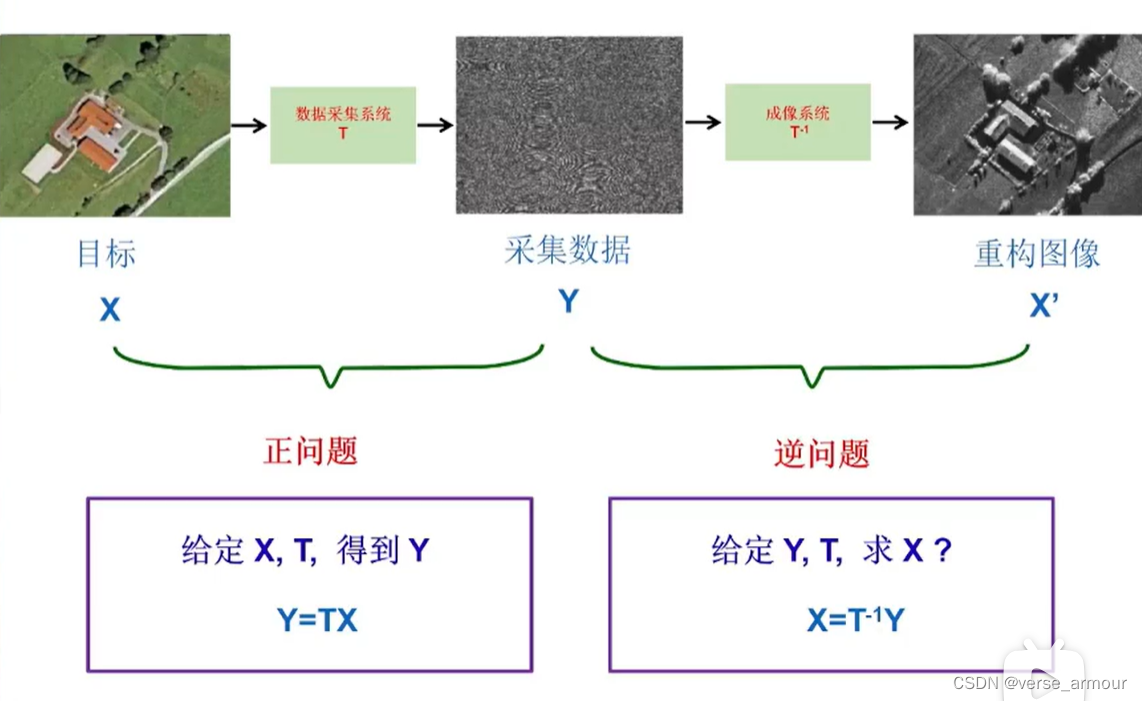
雷达成像研究的两个问题:正问题和逆问题
- 正问题:从被观测目标 X X X经过数据采集系统 T T T得到采集数据 Y Y Y。即给定 X X X, T T T,求解 Y Y Y。 Y = T X Y=TX Y=TX。
- 逆问题:从采集数据 Y Y Y经过成像系统 T − 1 T^{-1} T−1得到重构图像 X ′ X^{'} X′。即给定 Y Y Y, T T T,求解 X X X。 X = T − 1 Y X=T^{-1}Y X=T−1Y。
雷达设计的两大任务:数据采集和信息提取

数据采集: y = T x + n y=Tx+n y=Tx+n
算子
T
T
T由雷达的发射信号决定的,包括发射信号的波形 、极化方式、天线、发射信号调制。
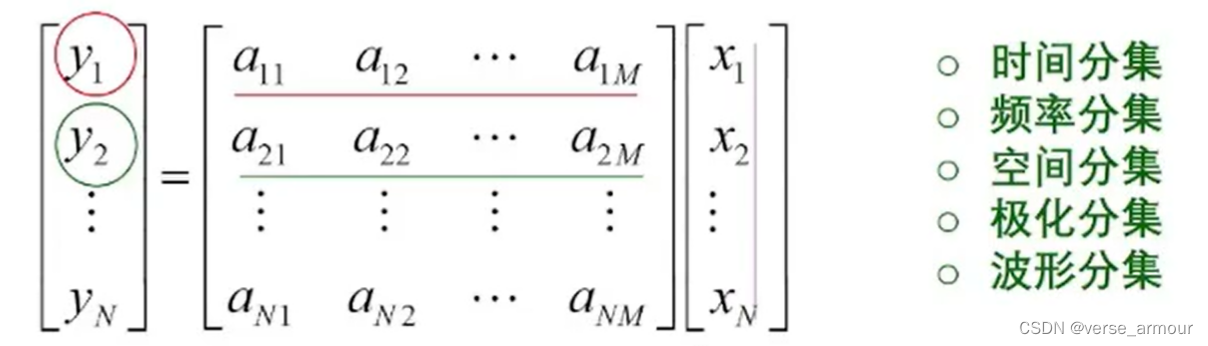
如何设计雷达的发射信号
T
T
T使得可以更好地提取信息
x
x
x?
(1)矩阵
T
T
T要满足每一行都不一样,因为有多少个未知数,就得有多少个方程,这样才能把未知向量
x
x
x解出来。
(2)最好的情况是矩阵
T
T
T是正交的,这样这个矩阵就没有冗余。
(3)放在雷达成像的背景下来理解:就是要设计的这个数据采集系统(观测方式)最好要使得我们每次的观测都不一样,这样才能最大化地获取这个目标的信息。最大化获取目标的信息才能方便重构目标图像,提高重构图像的精度。
信息提取: y − > x ? y->x? y−>x?
通常工程上对这个方程的求解认为是一个变态的问题。
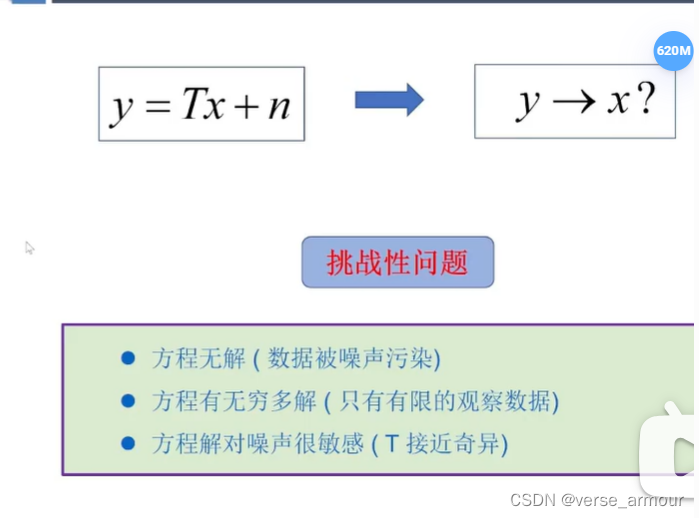
三个挑战性问题:
(1)方程无解(数据被噪声污染)
(2)方程有无穷多解(只有有限的观察数据)
任何一个观测目标都可以认为是一个无穷维度的向量,但是我们实际观察到的数据是有限维度的,即我们获得的方程的个数小于实际观测目标的维度(方程的个数少于未知数的个数),则该方程组有无穷多个解。
(3)方程解对噪声很敏感(
T
T
T接近奇异,行列式非常趋近于0)
此时,方程组有唯一解,但是这个解对噪声非常敏感。只要
T
T
T有一点噪声的扰动,这个解
x
x
x就会偏离真实值很大。
工程上对于无解的情况可以求出一个最小二乘解;无穷多个解的时候可以求出一个最小范数。比如我们去成像一个飞机,我们不需要得到一个显微镜级别的成像,我们只需要达到米级或者亚米级就够了,没有必要达到分子级或者原子级的精度,得到一个精确解。因此,在工程上,没有必要求出这个精确解。
二、SAR的多维理解
(1)雷达角度理解SAR
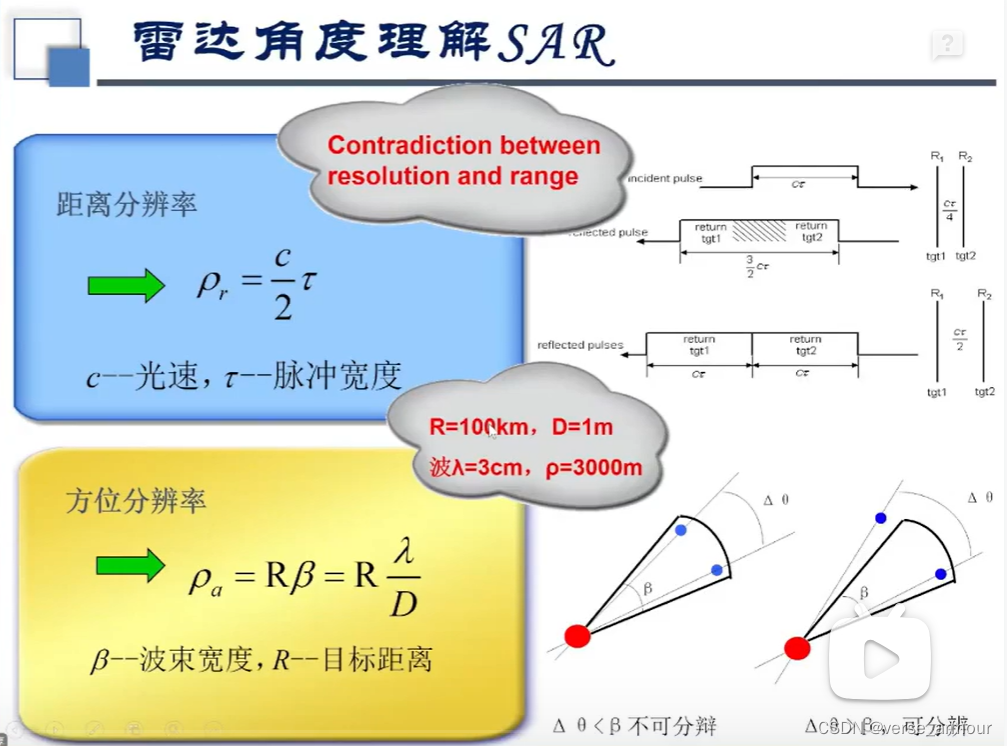
D
D
D表示天线的长度。如果想要方位分辨率达到1m,但是
R
=
100
k
m
,
λ
=
3
c
m
R=100km,\lambda=3cm
R=100km,λ=3cm保持不变,
D
=
3000
m
D=3000m
D=3000m。
实现困难:
- 3000m甚至30000m的天线孔径在物理上很难实现
- 即使实现了也很难在飞机、导弹、卫星上应用
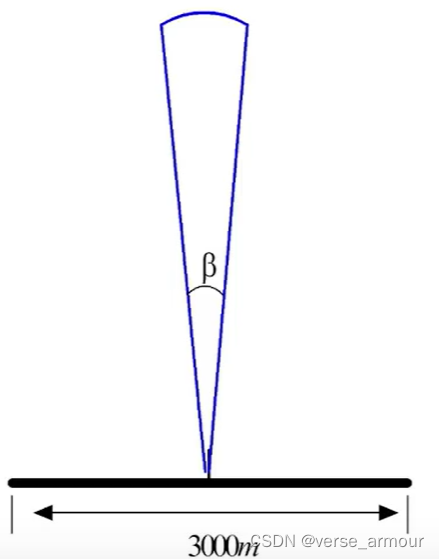
SAR是如何解决这个问题的呢?
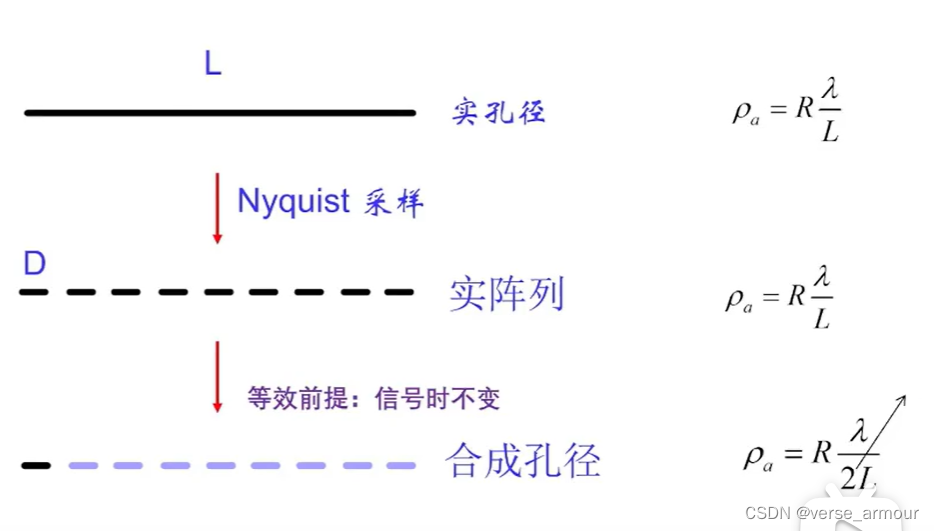
- 在空间中将天线孔径通过Nyquist采样离散化。
- 实阵列:得到的实阵列仍然不方便应用在飞机、导弹、卫星上,实阵列相当于在多个不同的角度观察,模拟了一个大的天线孔径的观察效果。(实孔径是一次就可以从不同角度去观察)
- 合成孔径:仅用实阵列中的一个小的天线孔径,去达到一系列实阵列的观察效果:用时间换空间。用一个天线孔径从不同的位置去观察。
等效前提:信号时不变。SAR成像关注的是地面目标,一般情况下地面目标在不同时间内的散射特性可以认为保持不变,满足信号时不变的前提。
(2)信号处理角度理解SAR
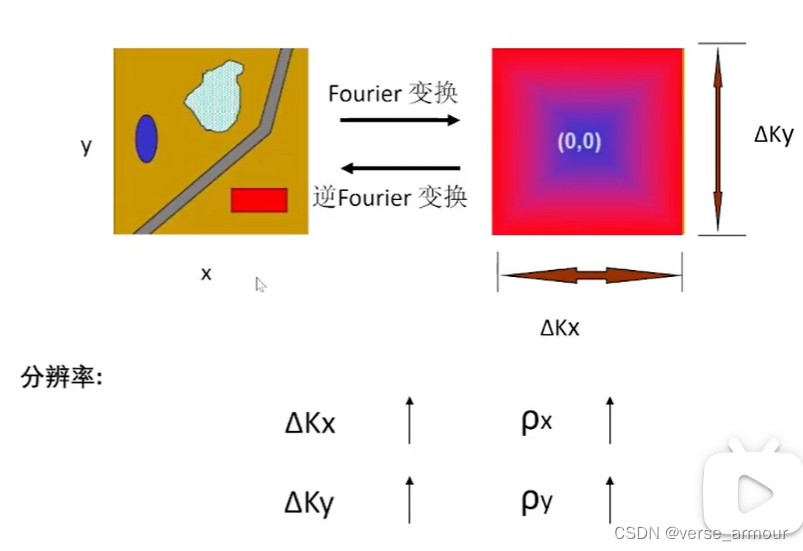
任何空域有限的信号,在频谱上是无限的。但是我们观察到的频谱又一定是有限的,通过有限的频谱作傅里叶逆变换很难重构出一个高精度的目标。
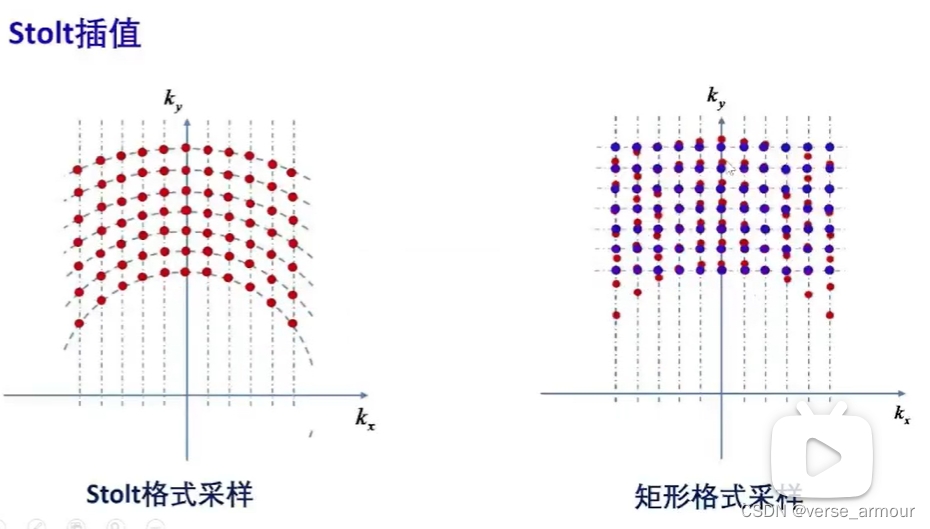
实际上我们去获取频谱的时候只能获取一些离散的采样值,可以是矩形格式采样,也可以是极坐标格式采样。
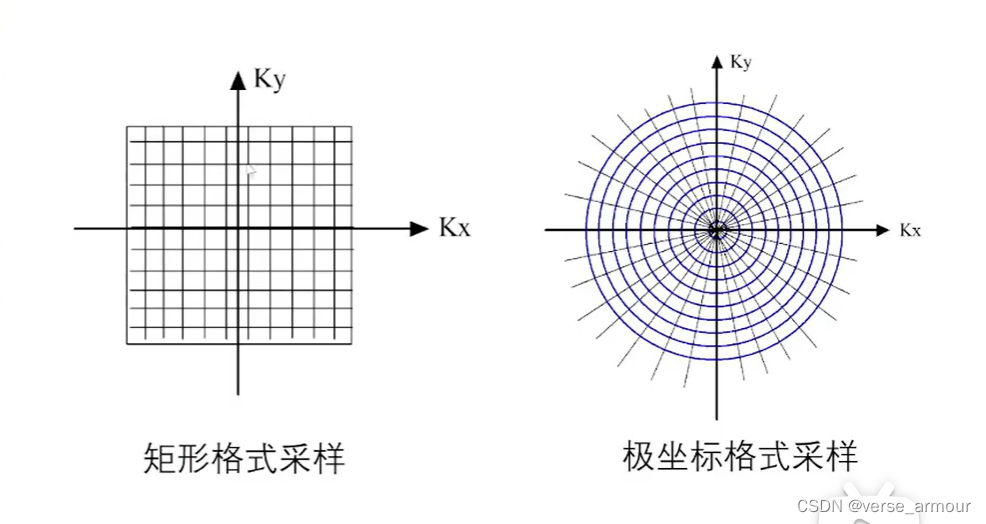
对于SAR成像采集到的信号,经过一定的预处理之后,得到的就是极坐标格式的采样。在极径上采样一定的范围,在极角上采样一定的范围。
在极径上采样的位置由载频决定,载频越高,在极径上的范围就越往外移;
在极径上采样的长度由发射带宽决定,发射信号的带宽越宽,在极径上采样的宽度就越宽;
在极角上采样的范围由雷达观测目标时的转角决定,转角越大,在频域上的采集的极角角度就越大。
聚焦上图,我们可以知道右图的载频大于左边的载频。在同样的极角下,范围更大,即方位分辨率更高。
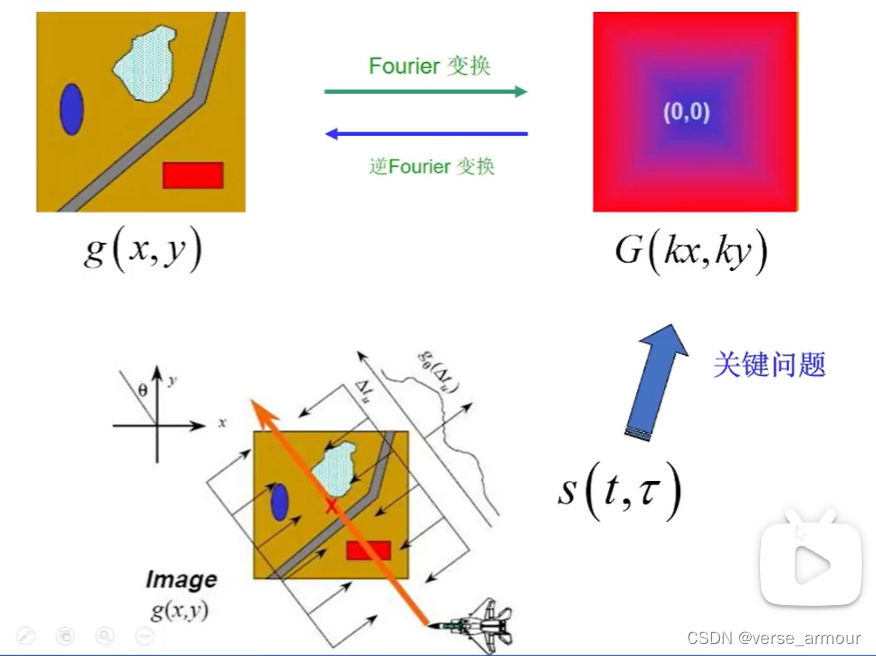
为什么可以从回波信号变换到两维频谱?为什么说回波信号就反映了频谱?——数学原理
这是因为,雷达的回波信号是发射信号和目标函数二维投影的卷积,即回波信号既包含发射信号的信息,也包含了投影的信息。但是发射信号只是一个工具,我们会从回波信号中将发现信号去掉,留下来的就是目标二维函数的一维投影的信息。将一维投影做一个傅里叶变换就可以得到两维频谱的切片。
单个脉冲只能得到一个角度的切片:
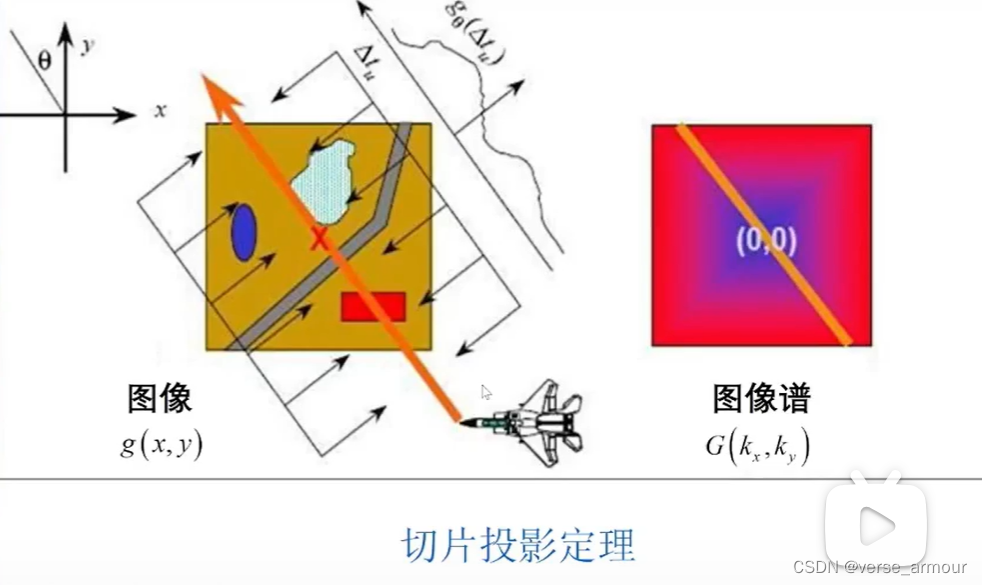
我们让雷达发射多个脉冲,可以得到不同角度的频谱切片。当我们得到足够多的切片时,我们就能得到一个较为完整的频谱。
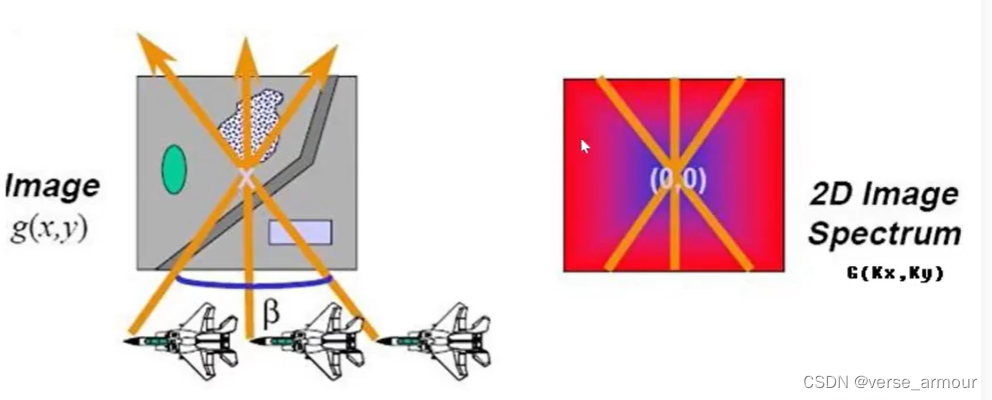
具体的算法实现可能会不一样。
(3)数学角度理解SAR
离散情况
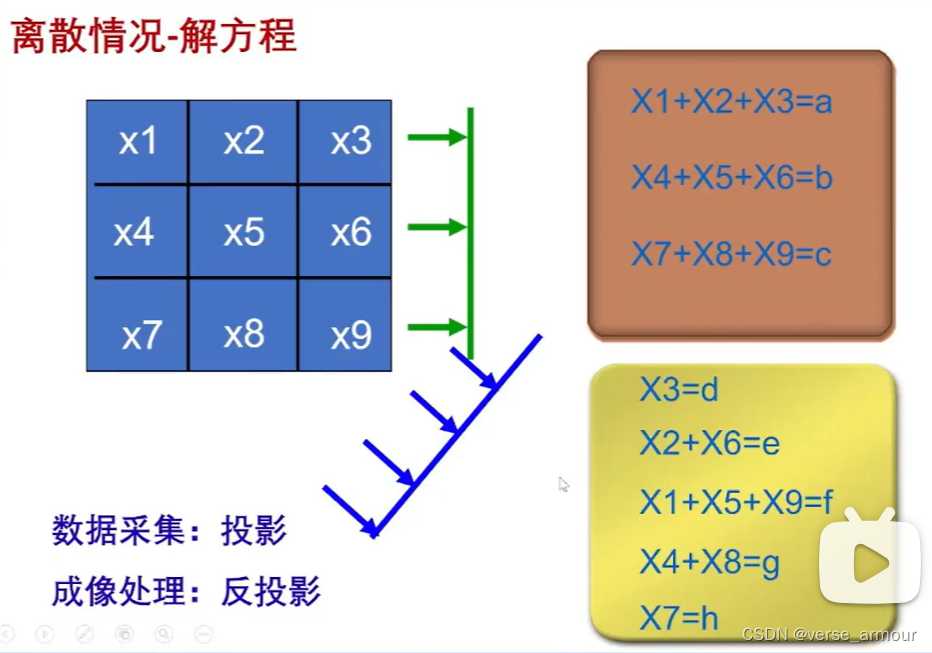
- 数据采集的过程就是投影值测量的过程
- 重构图像的过程就是解不同角度列的投影值方程组成的方程组过程(这只是数学角度的一个理解,真正工程上去实现的时候,方程组的维度特别大,所以不会有人真的去解这个方程组)
离散情况重构图像:反投影算法
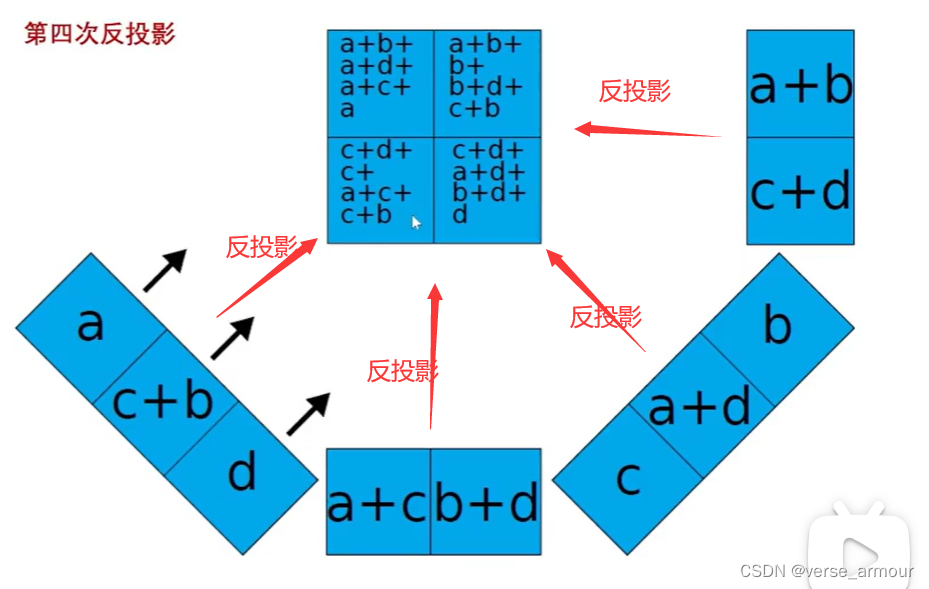
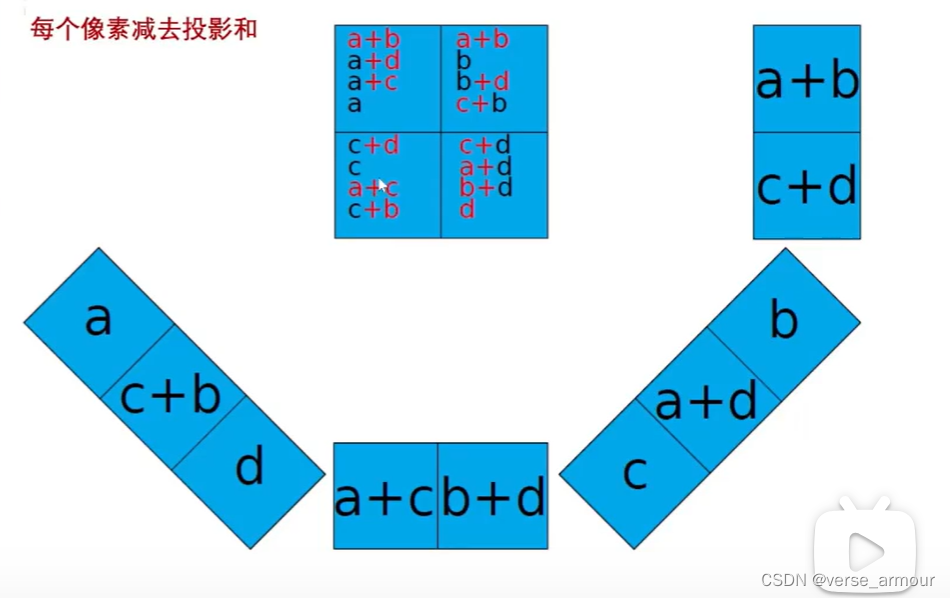
在SAR成像中,加完了就相当于抵消掉了。去掉之后剩下,3a,3b,3c,3d,和原来的就相差一个比例系数。
连续情况
连续情况重构图像:Randon变换和反变换
- 数据采集:Radon变换的过程
- 图像重构:Radon反变换的过程
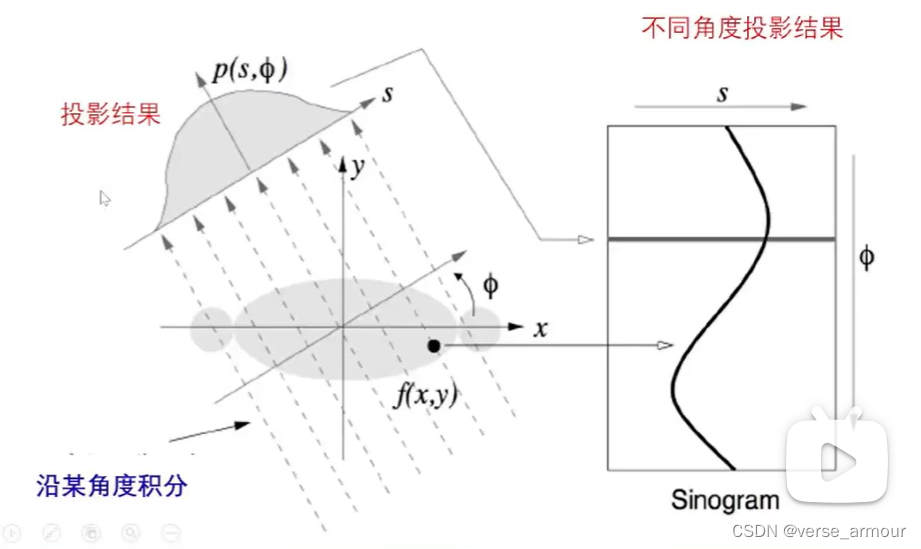
在传统的Radon变换中,通常是沿着一条直线去投影;但是在SAR成像中,一般是沿着一条弧形去投影。
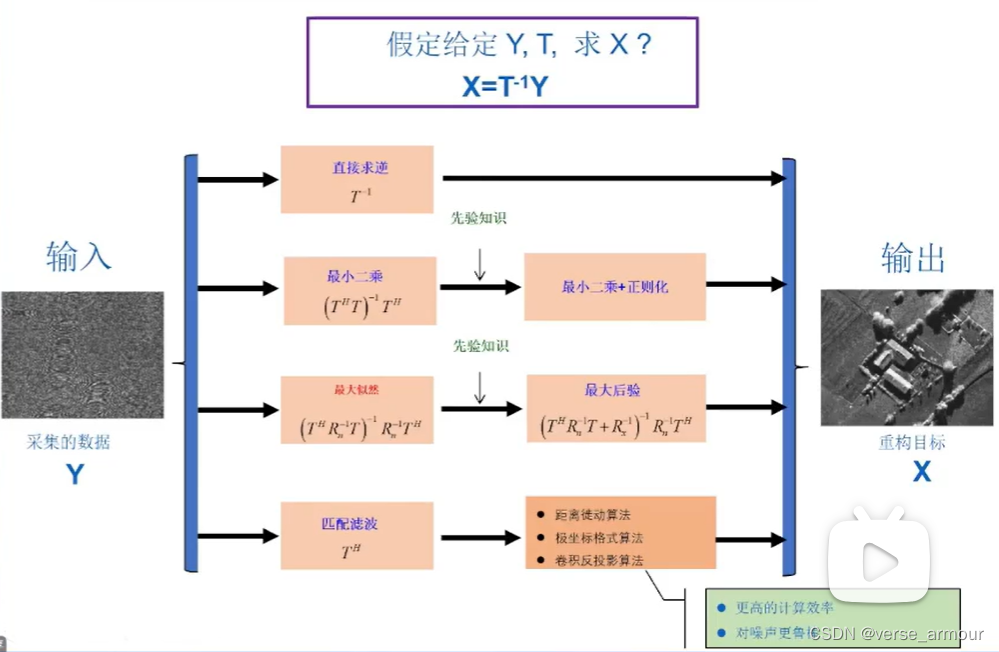
工程上一般会避免矩阵求逆(计算量大,鲁棒性差)来求 X X X,一般会用匹配滤波来实现。但这一定程度上牺牲了图像重构的精度。
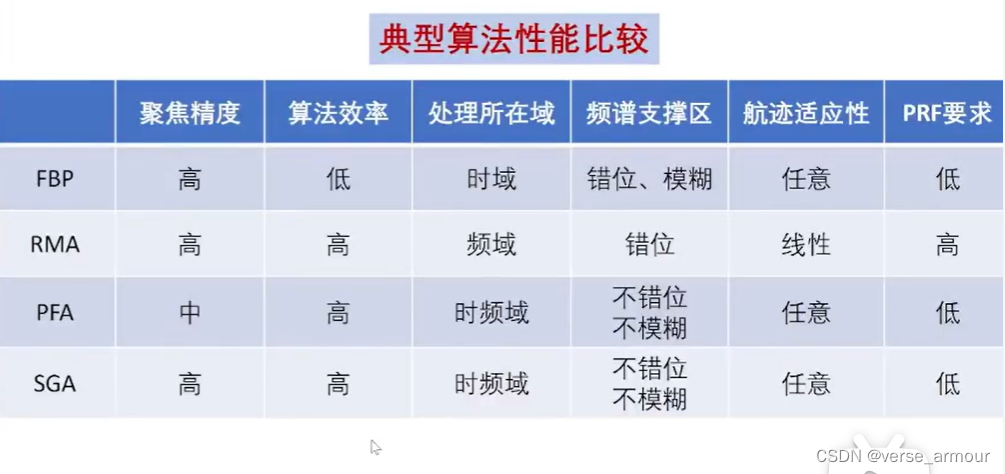
三、SAR成像算法的统一解释
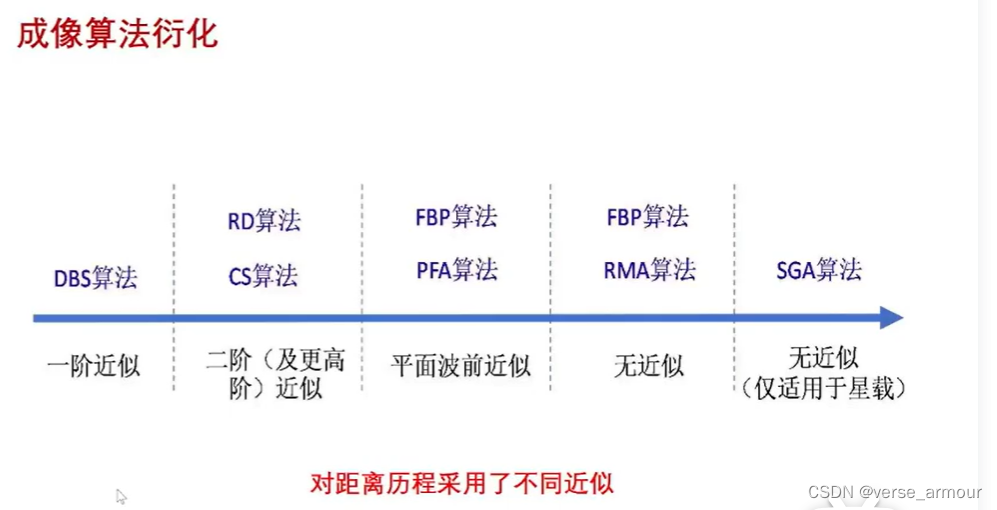
这些算法的本质都是匹配滤波,不同点在于对距离历程采用了不同近似
适用于星载的SGA算法比较好地解决了轨道弯曲、轨道非共面等问题,没有对任何距离历程采取近似。
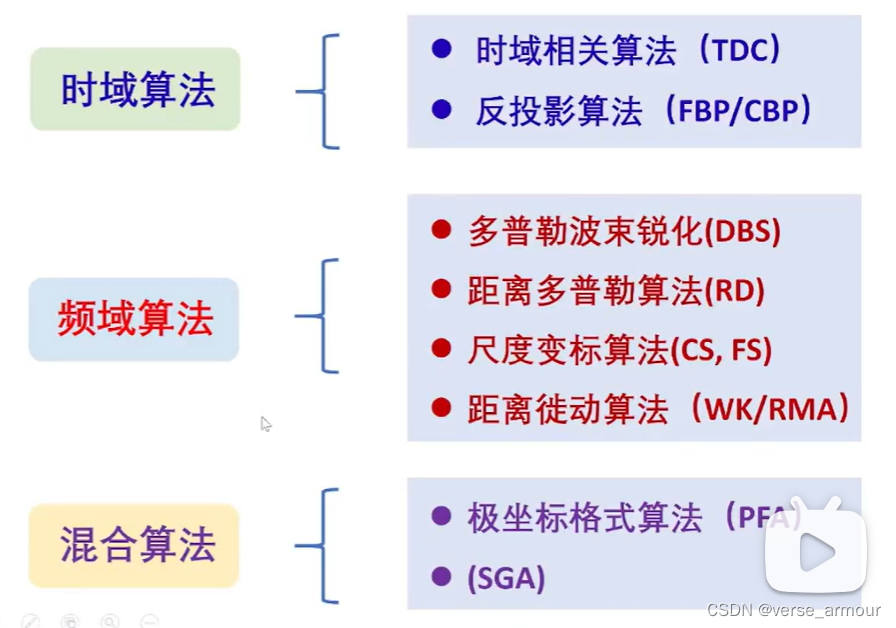
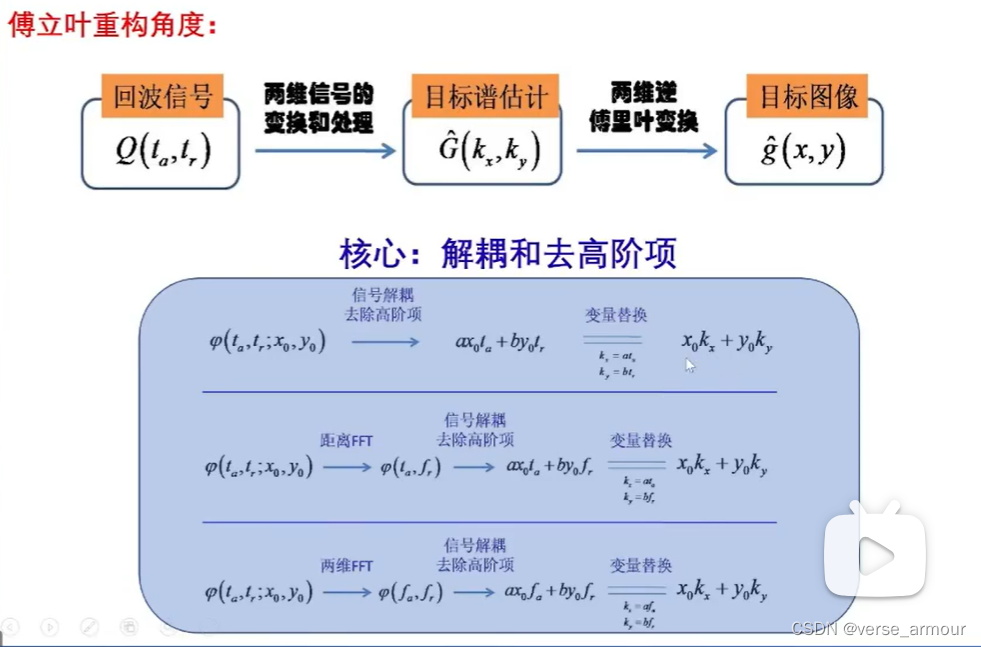
(1)极坐标格式算法
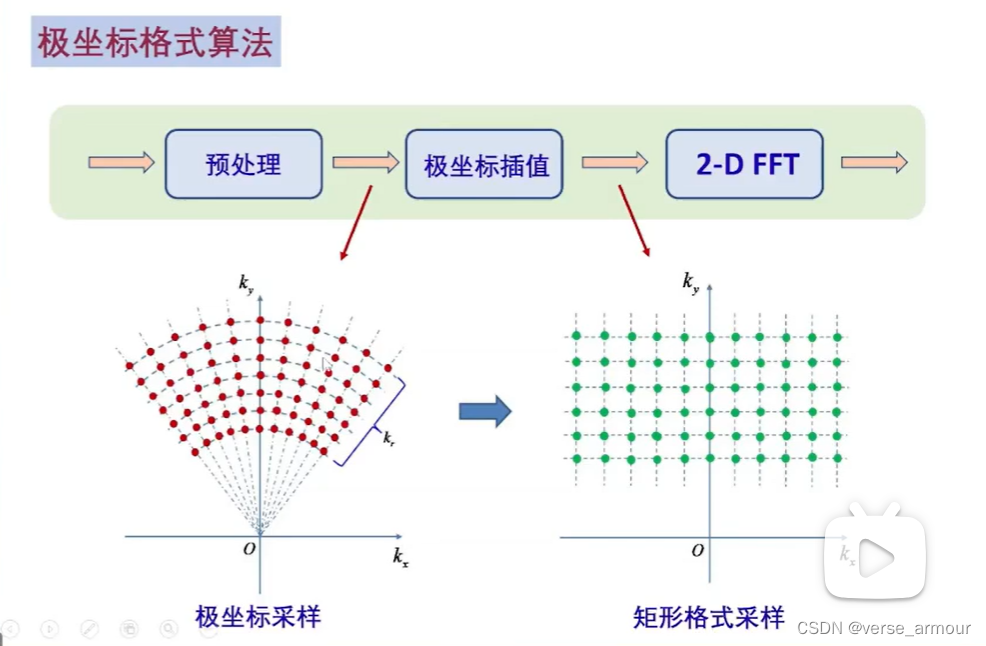
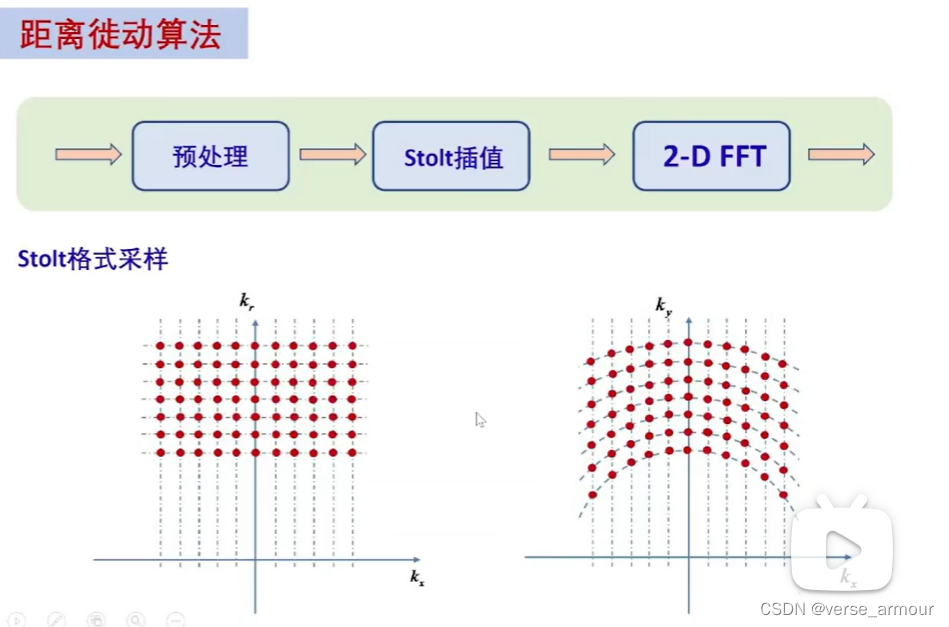
将极坐标采样通过一个重采样得到矩形格式采样,这样方便使用2-D FFT来进行图像重构。
极坐标格式转换
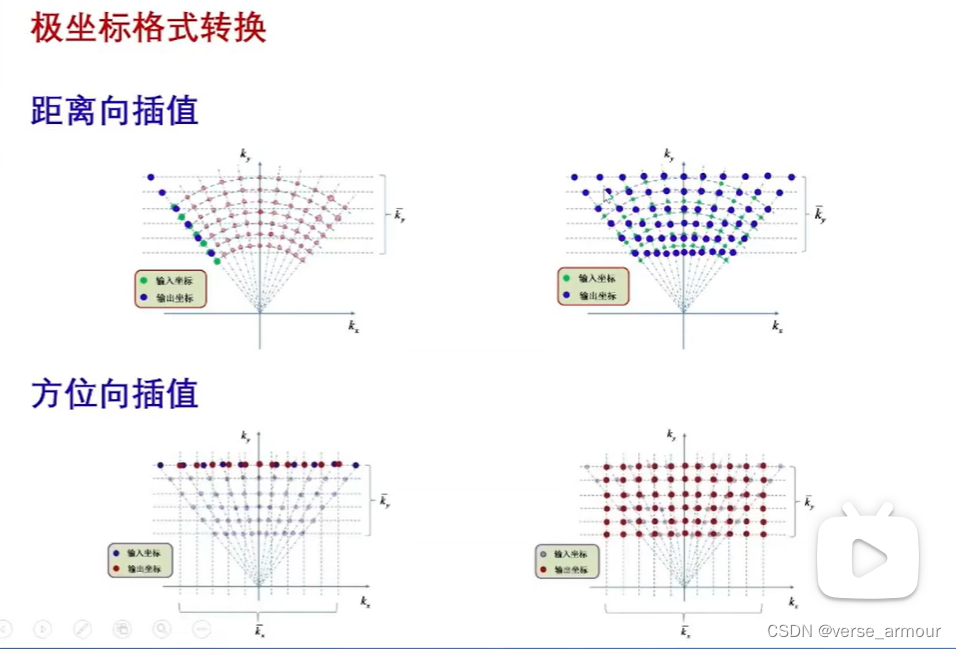
(2)距离徙动算法
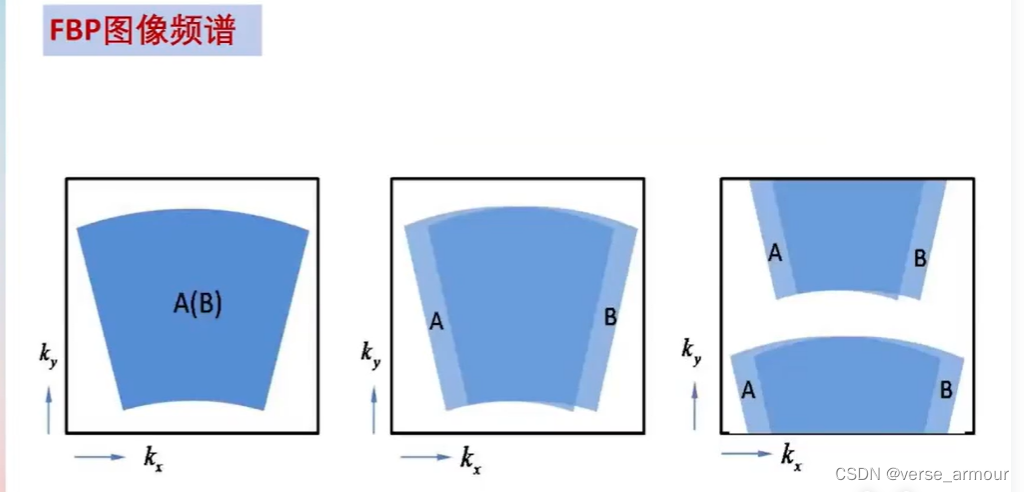
(3)卷积反投影算法
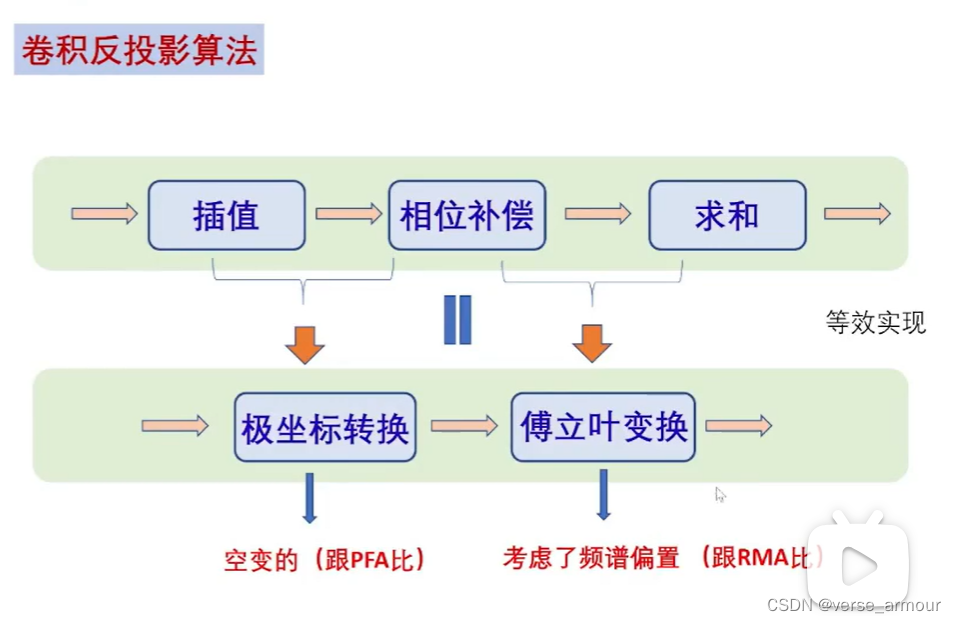
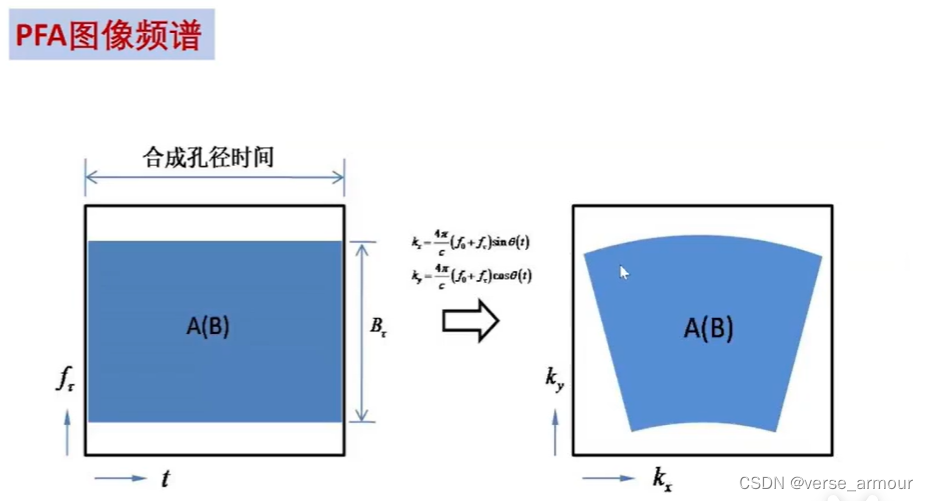
PFA算法认为对于场景中不同点的频谱都是一样的。但其实这是不准确的,空间中每个点的两维频谱是不一样的,这也便于理解为什么极坐标格式算法(PFA)是近似的。
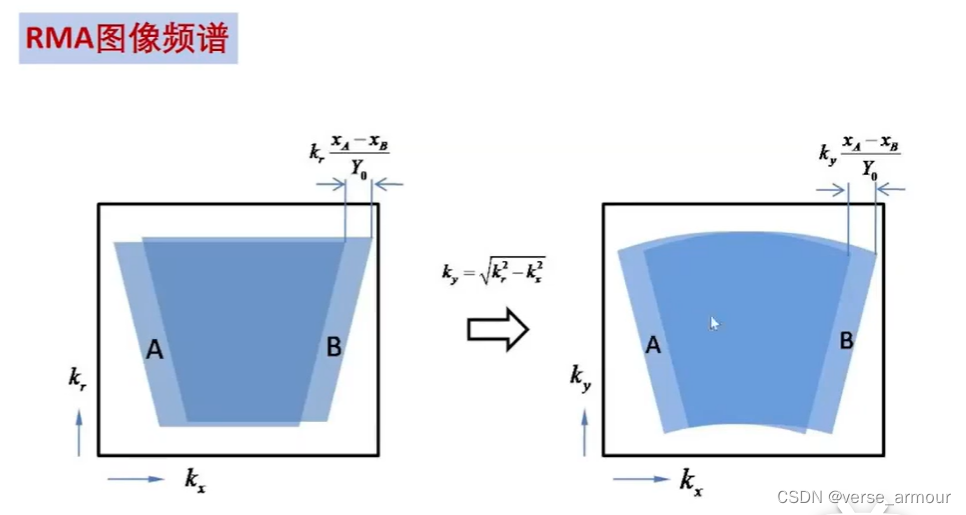
主要考虑了方位不同的点,频谱会在方位上有一个错位。


![[数据集][目标检测]纸箱子检测数据集VOC+YOLO格式8375张1类别](https://img-blog.csdnimg.cn/direct/4283cc21363b4ee6a66a143e40c4bc2f.png)


![NSSCTF | [SWPUCTF 2021 新生赛]easyupload2.0](https://img-blog.csdnimg.cn/direct/e7365ddaee994c438241ceeb7eab363d.png)