前言

上一篇文章我们刚刚学完二叉树初阶的相关知识，那接下来我们就趁热打铁，这篇文章，我们一起来看几道二叉树相关的OJ练习。

1. 单值二叉树

把题目链接给大家，供大家练习链接: link
我们一块看一下题：

思路分析

题目让我们干啥呢？

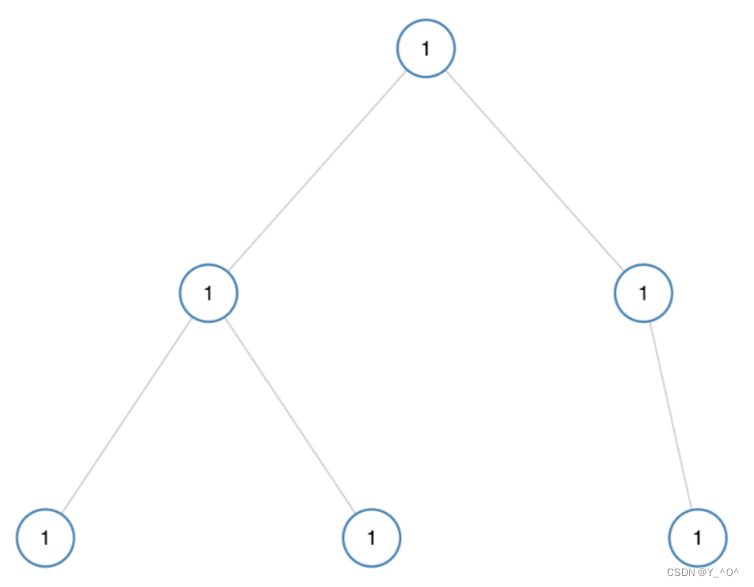
给定一棵二叉树，我们要写一个程序判断出它是不是一棵单值二叉树（即所有结点的值都相同的二叉树）。

应该怎么搞？

思路1. 遍历对比

首先第一种思路，就非常简单粗暴，我们可以记录一下根结点的值，然后，遍历这棵二叉树，去拿每个结点的值与根结点做对比，如果都相等，那就证明它是一棵单值二叉树，返回true；
一旦有一个不相等，那就证明不是，返回false。

这种方法呢我们就不实现具体的代码了，有兴趣大家可以自己写一下，接下来看另一种思路。

思路2. 递归

🆗，二叉树的结构我们还是更适合用递归的思想来搞。
以题目给的这棵二叉树为例：

首先要知道在这里如果是空树我们也应该认为它是一棵单值二叉树。
然后如果不是空，我们就开始判断，怎么判断？
如果根结点的值等于其左右结点的值，那就证明当前这几个结点是满足的，当然左右子树可能为空，为空的话就不比较了，只比较存在的那一边；
然后，去递归比较它的左右子树，还是同样的方法去比较，如果左右子树也满足，就返回true，有不满足的就false。

代码实现

写代码的时候呢，我们也有两种方式：

第一种就是按照上面的思想写出相等的情况，进行判断

bool isUnivalTree(struct TreeNode* root){
    if(root)
    {
        if(root->left&&root->right)
        {
            if((root->val==root->left->val)&&(root->val==root->right->val))
            {
                bool ret1=isUnivalTree(root->left);
                bool ret2=isUnivalTree(root->right);
                if(ret1&&ret2)
                    return true;
            }
            return false;
        }
        if(root->left)
        {
            if((root->val==root->left->val))
            {
                if(isUnivalTree(root->left))
                    return true;
            }
            return false;
        }
        if(root->right)
        {
            if((root->val==root->right->val))
            {
                if(isUnivalTree(root->right))
                    return true;
            }
            return false;
        }
    }
    return true;
}

但是：

这样去判断成立的情况写着有点麻烦，所以我们可以判断不成立的情况：

bool isUnivalTree(struct TreeNode* root){
    if(root)
    {
        if(root->left&&root->val!=root->left->val)
            return false;
        if(root->right&&root->val!=root->right->val)
            return false;
        return isUnivalTree(root->left)&&isUnivalTree(root->right);
    }
    return true;
}

这样代码就简洁很多。

2. 判断两棵二叉树是否相同

题目链接: link

思路分析

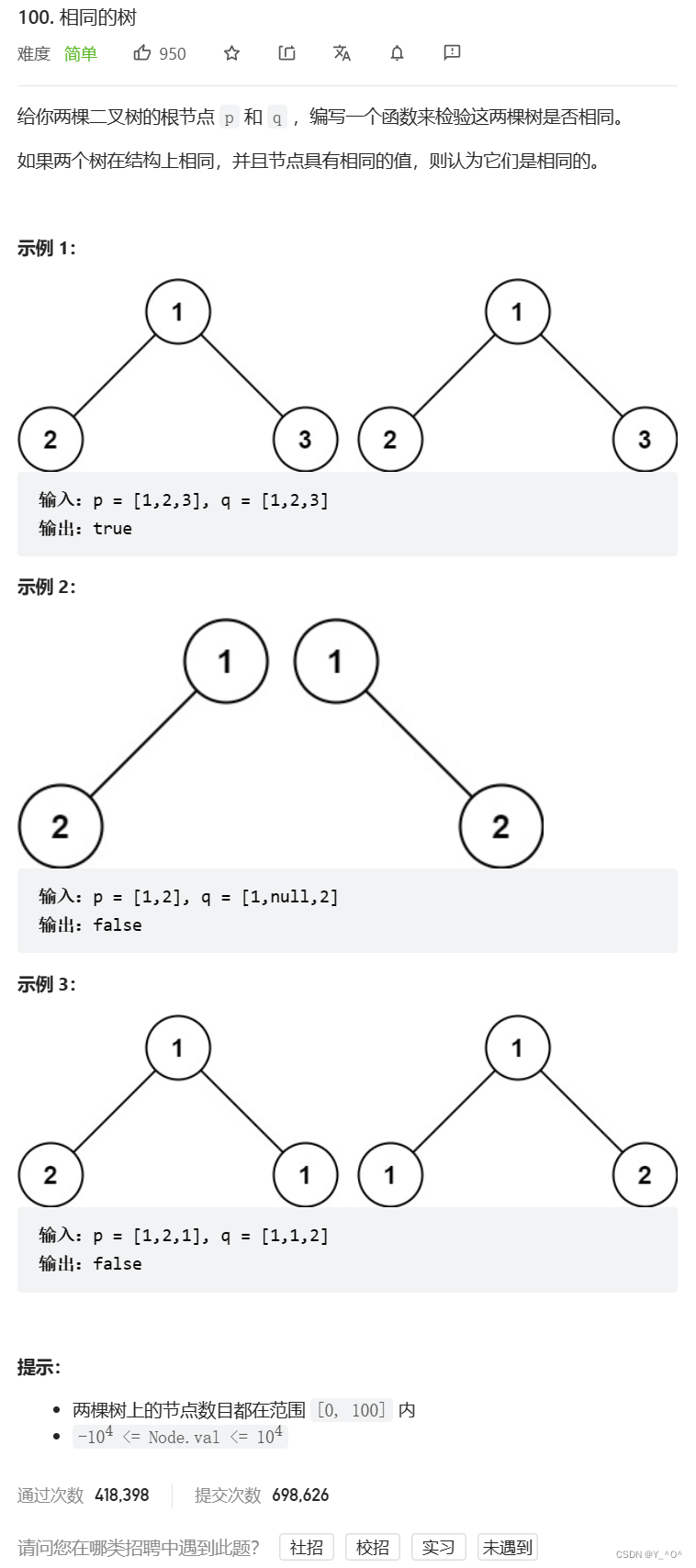
这道题呢，是给我们两棵二叉树的根结点，我们的程序要能够判断出这两棵二叉树是否相同（这里的相同指两个树结构相同，且对应结点的值相同）。

下面我们讲一下思路：

还是递归：
被对比的两棵二叉树有一下3种情况：

1. 两棵树都不为空
   这时我们先判断根结点的值是否相同，不相同直接返回false；
   如果相同，就要继续比较，怎么比？
   递归判读如果两棵树的左子树相同且右子树相同，那么两棵树就完全相同，左右子树有一个不相同就返回false。
2. 两棵中有一棵为空，一棵不为空
   不管是一开始两棵中有一棵为空，还是在递归过程中一棵空，一棵不为空，那两棵树都不可能相同了，返回false。
3. 两棵树都为空
   都是空树也算相同，返回true

代码实现

bool isSameTree(struct TreeNode* p, struct TreeNode* q){
    //p,q都不为空
    if(p&&q)
    {
        if(p->val!=q->val)
            return false;
        return isSameTree(p->left,q->left)
        &&isSameTree(p->right,q->right);
    }
    //p,q都为空
    if(p==NULL&&q==NULL)
        return true;
    //p,q有一个空
    return false;
}

3. 另一棵树的子树

题目链接: link

思路分析

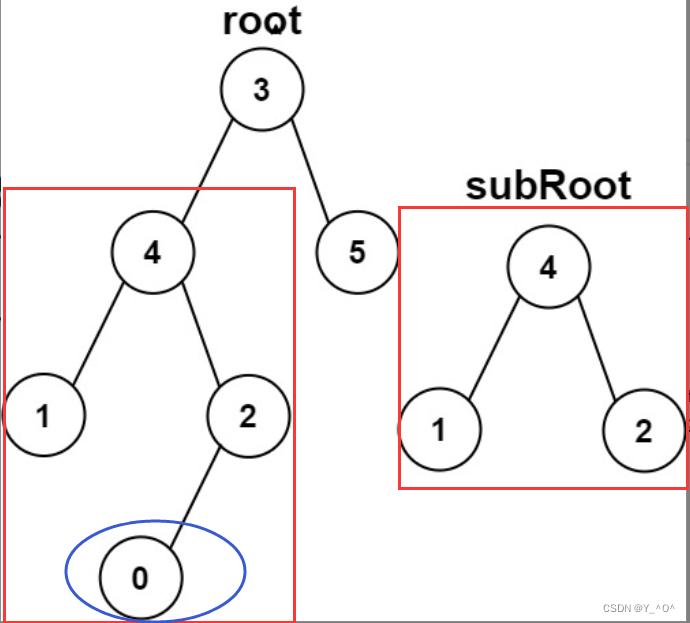
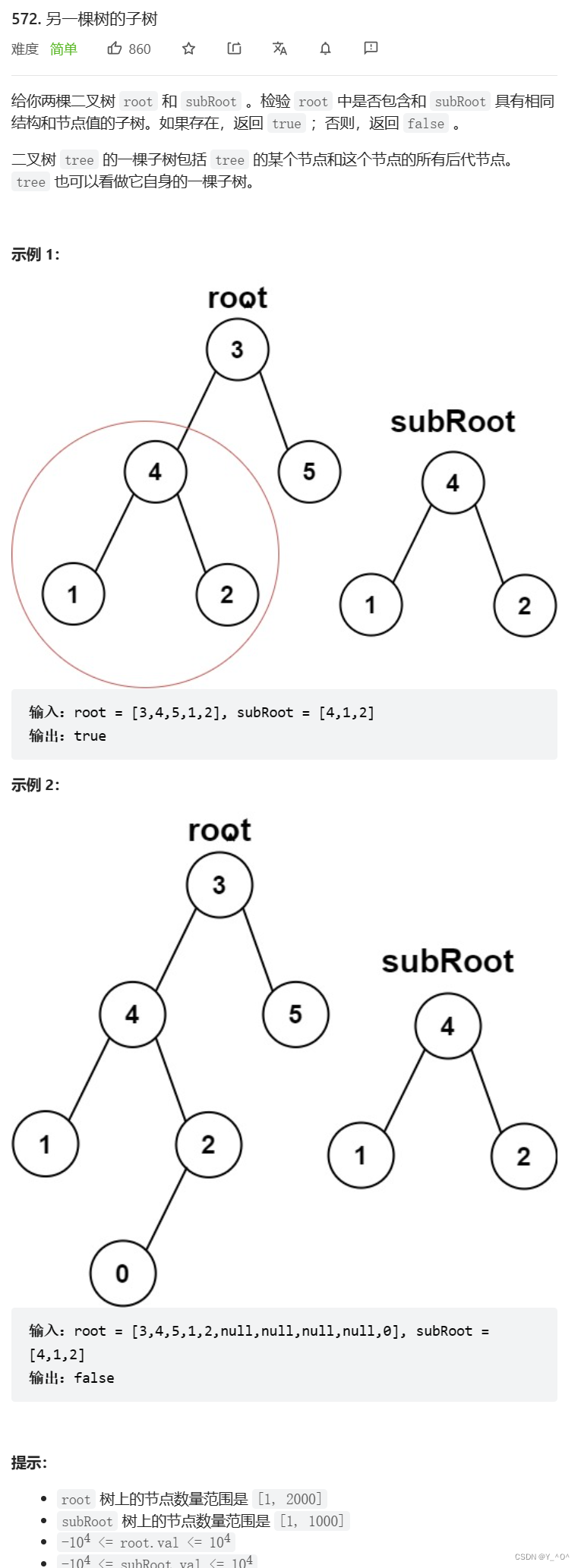
这道题也是给我们两棵二叉树，这次是让我们判断第二棵树是不是第一棵树的子树。
首先题目中需要注意的是：

也就是说这种情况是不算的：

🆗，那这道题该怎么解决：

我们刚刚完成了第二道题，判断两棵树是否相同，那现在再去做这个题是不是就很省事了啊。
我们可以遍历第一棵树，将第一棵树每一个结点对应的子树都与第二棵树进行比较，如果有一个相同的，那就说明第二棵树是第一棵树的子树。（判断两棵树是否相同直接复用上一题的代码）

代码实现

bool isSameTree(struct TreeNode* p, struct TreeNode* q){
    //p,q都不为空
    if(p&&q)
    {
        if(p->val!=q->val)
            return false;
        return isSameTree(p->left,q->left)
        &&isSameTree(p->right,q->right);
    }
    //p,q都为空
    if(p==NULL&&q==NULL)
        return true;
    //p,q有一个空
    return false;
}

bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){
    if(root)
    {
        if(isSameTree(root,subRoot))
            return true;
        return isSubtree(root->left,subRoot)||isSubtree(root->right,subRoot);
    }
    return false;
}

根据题目subroot是不为空的，所以root为空时两者不可能相同。

4. 返回二叉树结点的前序遍历数组

题目链接: link

思路分析

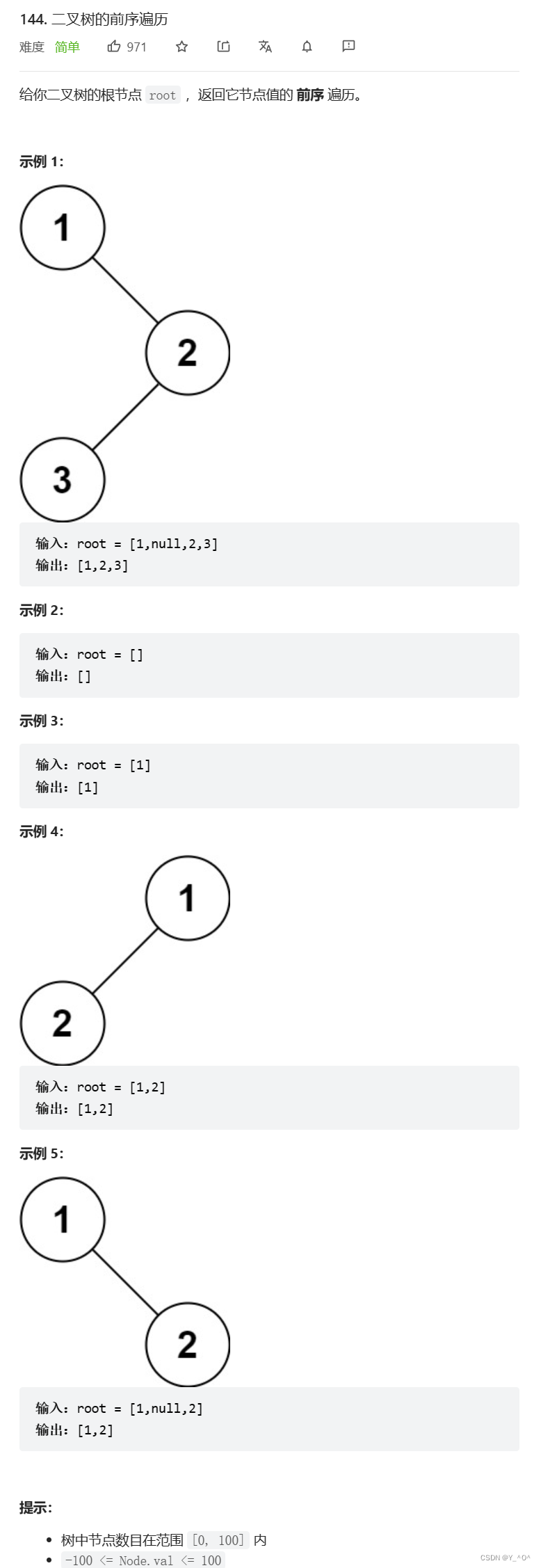
这道题呢在leetcode上的名字是二叉树的前序遍历，但是跟我们平时正常的前序遍历还不太一样。
我们之前的前序遍历是打印一下结点，但这道题要求我们把二叉树的结点以前序遍历的顺序放到一个数组中，然后返回这个数组。
并且呢，题目要求：

这个数组必须是malloc的。

那怎么搞呢？

既然要放在数组里，我们肯定要先定义一个数组，那数组应该开多大呢？
我们可以直接开一个大小100的。

因为题目明确了结点个数在100以内。
但是我们最终还是要知道数组的大小，因为题目给的接口函数还提供了另一个参数：

这个参数就是用来获取数组大小的，虽然题目没有明确要求让我们返回数组的大小。

所以：

我们就干脆单独写一个求结点个数的函数，这个我们上一篇文章刚学过，简简单单：

 //计算树的结点个数
 int TreeSize(struct TreeNode* root)
 {
     return root==NULL?0:
     TreeSize(root->left)+TreeSize(root->right)+1;
 }

那求完结点个数，参数returnsize的值我们就知道了，数组我们也可以malloc开辟了：

那接下来就是前序遍历结点放到数组里了

那还是用递归啊，但是直接在preorderTraversal函数里进行递归可以吗，好像不行，如果直接拿preorderTraversal函数递归，还有returnsize这个参数，还有malloc开辟的数组，好像没法搞。
那怎么办？

干脆再写一个函数来单独处理这个数组。

那要完成的工作就是前序遍历二叉树，按顺序把结点放入数组就行了。
这还不简单，不就写个前序遍历嘛，只不过不是打印结点，而是把结点的值存到数组中。

思路理清，我们来写一下代码

代码实现

 //计算树的结点个数
 int TreeSize(struct TreeNode* root)
 {
     return root==NULL?0:TreeSize(root->left)+TreeSize(root->right)+1;
 }

//前序遍历树的结点放入数组
void preorder(struct TreeNode* root,int* arr,int* pi)
{
    if(root)
    {
        arr[(*pi)++]=root->val;
        preorder(root->left,arr,pi);
        preorder(root->right,arr,pi);
    }
}

int* preorderTraversal(struct TreeNode* root, int* returnSize)
{
    *returnSize=TreeSize(root);
    int* arr=(int*)malloc(*returnSize*sizeof(int));
    int i=0;
    preorder(root,arr,&i);
    return arr;
}

5. 对称二叉树

题目链接: link

思路分析

我们一起来分析一下这道题：

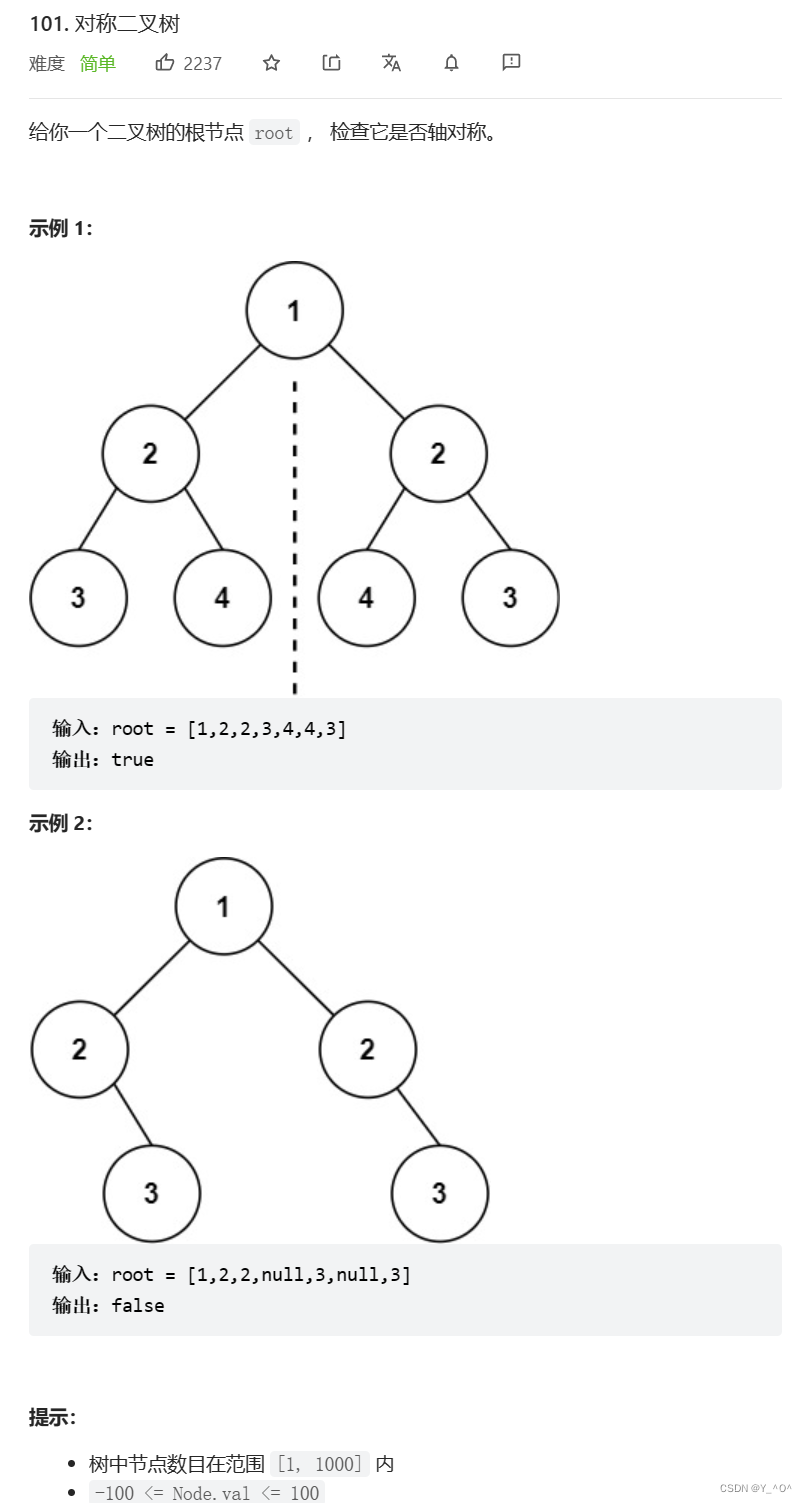
题目呢是让我们去判断一棵二叉树是否是对称二叉树。
🆗，那怎么判断，是判断它的左右子树相同吗？
不是的。
对称二叉树的特点是什么呢？

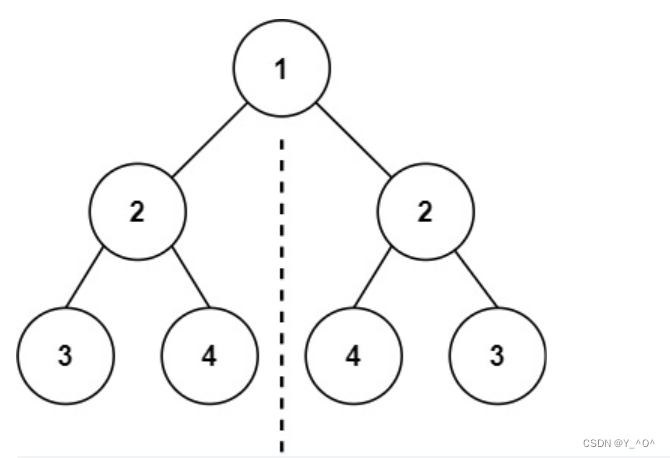
我们仔细观察可以发现：
对于对称二叉树来说，对称轴左边的子树和右边的子树，满足的是左子树的左孩子和右子树的右孩子对称，而左子树的右孩子和右子树的左孩子对称。
所以我们判断一棵二叉树是不是对称二叉树，不是判断它的左右子树是否相同，而应该反着比，看一个结点的左子树是不是和另一个结点的右子树对称。

我们拿到的是一棵二叉树的根，那我们是不是只需判断它的左右子树是否对称就行了啊。
所以呢，我们再搞一个子函数出来，专门用来判断两棵树是否对称。

然后我们注意到：

题目说明了给的二叉树至少一个结点，不会是空树。
那我们就可以直接这样：

如果它的左右子树对称，那整棵树不就对称了嘛。

那接下来就来实现判断两棵树是否对称的子函数_isSymmetric就行了：

首先如果两棵树都为空，那这棵二叉树就只有一个根结点嘛，那也算对称的：

如果其中有一个不为空，另一个为空，那肯定就不对称了：

那再往下，就是两棵树都不为空了，那首先是不是要判断它们的根结点对应的值想不想同啊，如果不相同，那也不对称：

那相同的话，是不是就要继续判断了，怎么判断？
那根据上面的分析，是不是要判断root1的左子树和root2的右子树是否对称，以及root1的右子树和root2的左子树是否相同。
如果都满足，那就是对称了

那就实现完了

代码展示

//判断两棵树是否对称
bool _isSymmetric(struct TreeNode* root1,struct TreeNode* root2){
    if(root1==NULL&&root2==NULL)
        return true;
    if(root1==NULL||root2==NULL)
        return false;
    if(root1->val!=root2->val)
        return false;
    return _isSymmetric(root1->left,root2->right)
        &&_isSymmetric(root1->right,root2->left);
}

bool isSymmetric(struct TreeNode* root){
    return _isSymmetric(root->left,root->right);
}

以上就是几道与二叉树相关的OJ练习。