送给大家一句话:
我们始终有选择的自由。选错了,只要真诚的反思,真诚面对,也随时有机会修正错误和选择。
– 《奇迹男孩(电影)》
💻💻💻💻💻💻💻💻
💗💗💗💗💗💗💗💗
⚜️从零开始构建二叉搜索树⚜️
- ✅1 前言
- ✅2 二叉搜索树(BST)
- 2.1 什么是二叉搜索树
- 2.2 二叉搜索树的功能
- ✅3 实现二叉搜索树
- 3.1 整体框架
- 3.2 插入功能
- 3.3 中序遍历
- 3.4 搜索功能
- 3.5 删除操作
- ✅4 应用一下
- Thanks♪(・ω・)ノ谢谢阅读!!!
- 下一篇文章见!!!
✅1 前言
在之前初阶数据结构的篇章中,我们学习过二叉树的基础知识稍微复习一下:
- 二叉树的度不超过 2
- 二叉树可以通过数组或链表结构记录(左孩子右兄弟法)
普通的二叉树没有特别的性质,今天我们就来赋予其一个全新的性质来满足高速搜索的需求 ,并为后序的map与set做铺垫 ,二叉搜索树的特性了解,有助于更好的理解map和set的特性
✅2 二叉搜索树(BST)
2.1 什么是二叉搜索树
二叉搜索树又称二叉排序树(BST),它或者是一棵空树,或者是具有以下性质的二叉树:
- 若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
- 若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
- 它的左右子树也分别为二叉搜索树
- 注意通常二叉搜索树不会有相同的键值
这些性质使得二叉搜索树成为一种高效的搜索工具。在大部分情况下,对于包含 n 个节点的二叉搜索树,搜索、插入和删除等操作的时间复杂度为 O(logn)。然而,在某些情况下,二叉搜索树可能会出现不平衡的情况,导致时间复杂度激增至 O(n)。为了解决这个问题,出现了进阶版的 AVL 树和红黑树。
AVL 树 和 红黑树 都是在保持二叉搜索树基本性质的基础上,通过旋转和重新平衡等操作,确保树的高度保持在一个相对平衡的状态,从而保证了操作的时间复杂度始终为 O(logn)。它们的出现大大提高了二叉搜索树在实际应用中的性能和稳定性。
我们常常会选择使用 AVL 树或红黑树来解决搜索问题。
今天,我们主要来学习二叉搜索树,为后序的学习打好基础!!!
2.2 二叉搜索树的功能
二叉搜索树(Binary Search Tree, BST)是一种非常实用的数据结构,用于存储具有可比较键的数据项。其功能和应用场景非常广泛,主要包括以下几点:
✨核心功能✨
- 🎈搜索:提供高效的搜索功能,允许快速查找特定键值的数据项。如果树保持平衡,搜索的平均时间复杂度可以保持在 O(log n)。
- 🎈插入和删除:允许在保持树结构的前提下添加和移除节点。插入和删除操作也尽量维持树的平衡,以避免性能下降。
- 🎈排序:可以中序遍历二叉搜索树以获得有序的数据序列,这对于数据排序和报表生成等功能非常有用。
✨应用场景✨
- 🎈数据库管理系统:许多数据库索引就是使用二叉搜索树或其变种(如B树、红黑树)来实现的,以便快速地查询和更新数据。
- 🎈符号表应用:在编译器实现中,二叉搜索树可以用来构建和管理符号表,以支持变量名的快速查找和属性的存取。
- 🎈优先队列实现:通过特定方式实现的二叉搜索树(如二叉堆),可以用于实现优先队列,支持快速插入元素和删除最小或最大元素的操作。
接下来我们就根据其性质,来实现二叉搜索树 ❗ ❗ ❗
✅3 实现二叉搜索树
3.1 整体框架
🎇首先我们需要搭建一个整体的框架,设计节点结构体和二叉搜索树类
我们创建一个节点结构体:
- 包括左右指针
- 键值记录节点值
二叉搜索树类仅需要需要一个根节点足矣!
//节点结构体
template<class K>
struct BSTreeNode
{
//构造函数
BSTreeNode(K key = 0)
: _key(key),
_right(nullptr),
_left(nullptr)
{
}
//左右指针
BSTreeNode* _right;
BSTreeNode* _left;
//键值
K _key;
};
//树的结构
template<class K>
class BSTree
{
public:
typedef BSTreeNode<K>* Node*;
private:
Node* _root = nullptr;
};
有了框架,我们就来逐个实现功能!!!
3.2 插入功能
❤️🔥根据二叉搜索树的性质来寻找到合适的位置即可,注意:
- 需要一个当前节点指针和父节点指针,因为插入需要父节点来进行!!!
- 如果根节点为空指针,那么直接赋值给根节点就可以
- 小于当前键值就放左边,大于当前键值就放右边,直到找到合适位置
void Insert(K key)
{
//先判断是否为空
if (_root == nullptr)
{
_root = new BSTreeNode<K>(key);
}
//不为空 就寻找合适位置进行插入
else
{
Node* cur = _root;
Node* parent= nullptr;
//寻找合适位置
while (cur != nullptr)
{
//小于当前键值就放左边
if (key < cur->_key)
{
parent = cur;
cur = cur->_left;
}
else
{
parent = cur;
cur = cur->_right;
}
}
//创建节点
cur = new BSTreeNode<K>(key);
//已经找到合适位置:
//大于父节点就放在右边
if (key > parent->_key)
{
parent->_right = cur;
}
//反之放在左边
else
{
parent->_left = cur;
}
}
}
❤️🔥 这样就写好了,为了方便我们的调试,我们赶紧来写一个中序遍历!!!
3.3 中序遍历
递归版本的中序遍历很简单😎😎😎:
//嵌套一层来换行
void InOrder()
{
_InOrder(this->_root);
cout << endl;
}
//中序遍历
void _InOrder(Node* cur)
{
if (cur == nullptr) return;
_InOrder(cur->_left);
cout << cur->_key << " ";
_InOrder(cur->_right);
}
逻辑比较很好理解奥!!!
我们测试一下:
void BSTreeTest1()
{
BSTree<int> tree;
int arr[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };
for (auto s : arr)
{
tree.Insert(s);
}
tree.InOrder();
//cout << tree.Find(5) << endl;
//cout << tree.Find(1) << endl;
}
来看效果:

🎉🎉🎉🎉🎉🎉🎉🎉
👌👌👌,也验证了我们的插入没有问题了!!!
3.4 搜索功能
搜索功能直接套用刚才的插入就可以了
bool Find(K key)
{
//先判断是否为空
if (_root == nullptr)
{
return false;
}
//不为空 就寻找合适位置进行插入
else
{
Node* cur = _root;
while (cur != nullptr)
{
if (key == cur->_key)
{
return true;
}
//小于当前键值就在左边
else if (key < cur->_key)
{
cur = cur->_left;
}
//反之在右边
else
{
cur = cur->_right;
}
}
//没有找到
return false;
}
}
❤️🔥这样寻找就实现了❤️🔥
3.5 删除操作
⚠️前方高能预警⚠️
删除操作是二叉搜索树最关键,也是最复杂度的功能!!!
🔆🔆🔆先请来如来佛祖🔆🔆🔆
//大佛镇压bug
// _ooOoo_ //
// o8888888o //
// 88" . "88 //
// (| - - |) //
// O\ - /O //
// ____/`---'\____ //
// .' \\| |// `. //
// / \\||| : |||// \ //
// / _||||| -:- |||||- \ //
// | | \\\ - /// | | //
// | \_| ''\---/'' | | //
// \ .-\__ `-` ___/-. / //
// ___`. .' /--.--\ `. . ___ //
// ."" '< `.___\_<|>_/___.' >'"". //
// | | : `- \`.;`\ _ /`;.`/ - ` : | | //
// \ \ `-. \_ __\ /__ _/ .-` / / //
// ========`-.____`-.___\_____/___.-`____.-'======== //
// `=---=' //
// ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ //
// 佛祖保佑 永无BUG 永不修改 //
我们不能轻举妄动,先来分析一下可能会出现的情况:
- 首先我们要找到被删除的节点
- 然后是删除,这个删除不能随便删除奥,先分析一下可能出现的情况:
- 1️⃣要删除的结点无孩子结点
- 2️⃣要删除的结点只有左孩子结点
- 3️⃣要删除的结点只有右孩子结点
- 4️⃣要删除的结点有左、右孩子结点
- 分析可能出现的情况,1️⃣2️⃣3️⃣可以归为一类A,4️⃣归为一类B
🎁先来看A类🎁
A类由于被删除的节点只有一边有节点,所以只需要把父节点指向它的指针指向它的子节点就可以!
但是要考虑一个特殊情况 ❗ ❗ ❗如果被删除的节点没有父节点(也就是删除根节点时),需要特殊处理:直接把根节点更新就可以
bool Erase(K key)
{
Node* cur = _root;
Node* parent = nullptr;
//首先需要找到需要删除的节点
while (cur != nullptr)
{
//小于当前键值就放左边
if (key < cur->_key)
{
parent = cur;
cur = cur->_left;
}
else if(key > cur->_key)
{
parent = cur;
cur = cur->_right;
}
//找到了
else
{
//A 类
if (cur->_left == nullptr || cur->_right == nullptr)
{
//因为有一边是没有元素的,所以只需要把父节点指向它的指针指向它的子节点
if (cur->_left == nullptr)
{
//没有父亲
if (parent == nullptr)
{
_root = cur->_right;
}
else if (cur == parent->_left) parent->_left = cur->_right;
else parent->_right = cur->_right;
delete cur;
}
else
{
//没有父亲
if (parent == nullptr)
{
_root = cur->_left;
}
//是左子节点,就改变父节点的左指针
else if (cur == parent->_left) parent->_left = cur->_left;
//是右子节点,就改变父节点的右指针
else parent->_right = cur->_left;
delete cur;
}
}
// B类!
else
{
//...
}
return true;
}
}
//没找到要删除的值就返回false
return false;
}
🎁再来看B类🎁
因为需要删除的节点左右指针都有值,所以不能通过上述的办法来进行操作!!!
所以采取替换法:
替换法:找一个值来替代当前值,因为不能原本的树的结构,所以要找到符合条件的值。根据二叉搜索树的性质可以找:左子树最大值或右子树最小值
🔅🔅🔅🔅🔅🔅
替换之后我们看图:
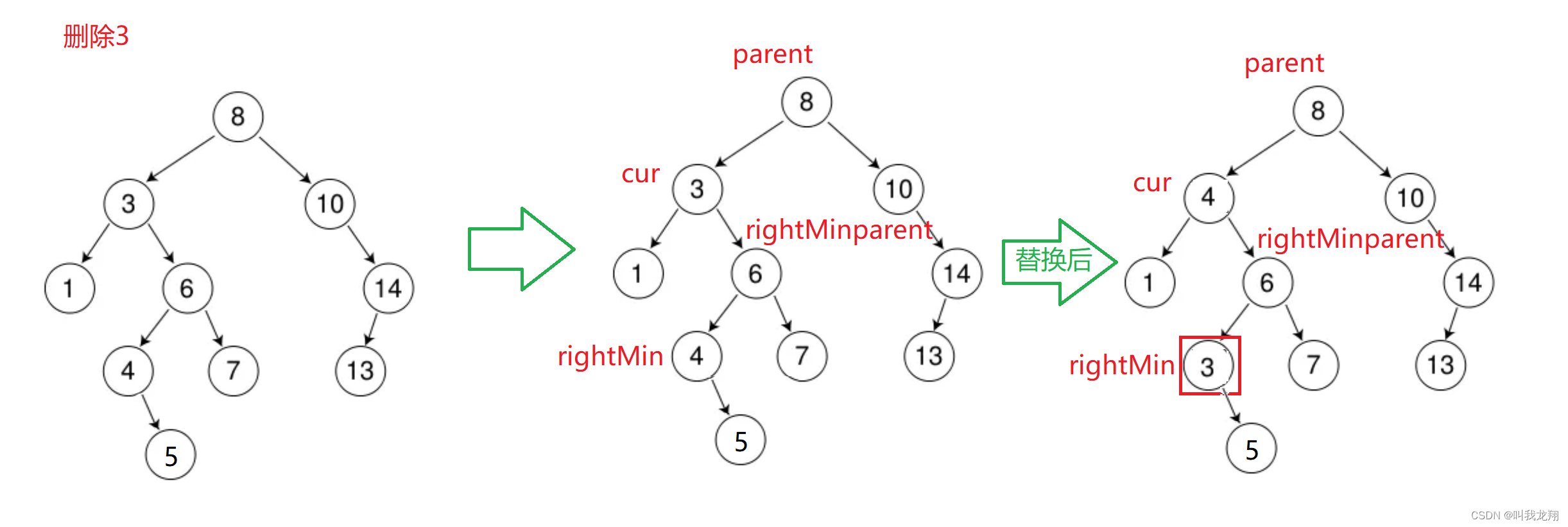
⚠️由于rightMin是右子树的最小值,那么它就不会有左子树,所以这时候时间将rightMinparent的指向它的指针指向它的子节点就可以。
//....
// B类比较复杂!
else
{
//这个情况需要找到该位置的替代值
//选择左子树的最大值 或 右子树的最小值
//这里我们选择右子树的最小值
Node* rightMin = cur->_right;
Node* rightMinparent = nullptr;
//寻找右子树的最小值
while (rightMin->_left)
{
rightMinparent = rightMin;
rightMin = rightMin->_left;
}
//找到最小值 -> 交换
swap(rightMin->_key, cur->_key);
//所以这时候不可以直接删除
//需要判断一下对应指针!!!
if (rightMinparent->_right == rightMin)
{
rightMinparent->_right = rightMin->_right;
}
else
{
rightMinparent->_left = rightMin->_right;
}
delete rightMin;
}
return true;
//...
再来看特殊情况:如果删除的是 8 (根节点)
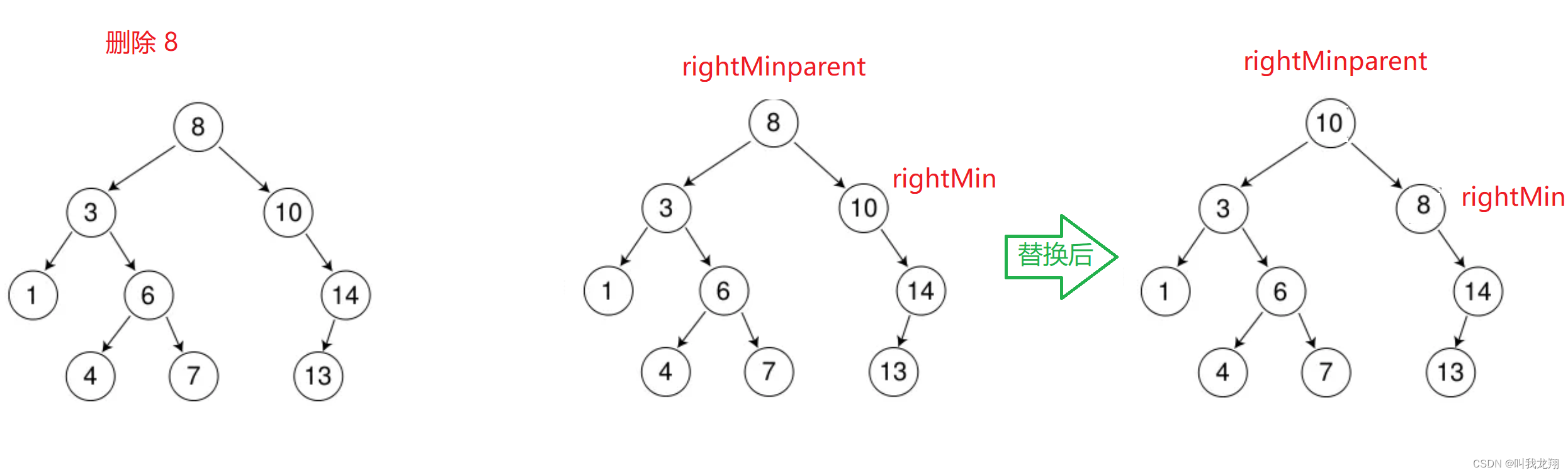
这样因为rightMin已经是右子树最小值了,所以不会进入查找循环,rightMinparent就不会被赋值,就出现野指针了,所以要给其赋初始值:
Node* rightMinparent = cur;
💯💯💯💯💯💯
这样就写好了!!!
测试一下:
void BSTreeTest2()
{
BSTree<int> tree;
int arr[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };
for (auto s : arr)
{
tree.Insert(s);
}
tree.InOrder();
for (auto s : arr)
{
tree.Erase(s);
tree.InOrder();
}
}
🎊来看效果🎊:

这样我们的二叉搜索树就完成了!!!
🤞🤞🤞
✅4 应用一下
刚才我们建立的是最简单的二叉搜索树,接下来我们可以将他应用到实践中:
- 😁K模型:K模型即只有key作为关键码,结构中只需要存储Key即可,关键码即为需要搜索到的值。
比如:给一个单词word,判断该单词是否拼写正确,具体方式如下:- 以词库中所有单词集合中的每个单词作为key,构建一棵二叉搜索树
- 在二叉搜索树中检索该单词是否存在,存在则拼写正确,不存在则拼写错误。
- 😍KV模型:每一个关键码key,都有与之对应的值Value,即<Key, Value>的键值对。该种方式在现实生活中非常常见:
- 比如英汉词典就是英文与中文的对应关系,通过英文可以快速找到与其对应的中文,英文单词与其对应的中文<word, chinese>就构成一种键值对;
- 再比如统计单词次数,统计成功后,给定单词就可快速找到其出现的次数,单词与其出现次数就是<word, count>就构成一种键值对
我们现在做一个水果统计的功能,我们就需要设置合适的 K V映射 (key-val)
template<class K , class V>
struct BSTreeNode
{
//构造函数
BSTreeNode(K key = 0 , V val = 0)
: _key(key),
_value(val),
_right(nullptr),
_left(nullptr)
{
}
//左右指针
BSTreeNode* _right;
BSTreeNode* _left;
//键值
K _key;
V _value;
};
其他代码也对应修改!!!
我们来测试一下:
void BSTreeTest3()
{
BSTree<string , int> countTree;
string arr[] = { "苹果", "西瓜", "苹果", "西瓜","草莓", "苹果", "苹果", "草莓","西瓜","苹果", "香蕉", "苹果", "香蕉" ,"草莓","芒果"};
for (const auto& str : arr)
{
// 先查找水果在不在搜索树中
// 1、不在,说明水果第一次出现,则插入<水果, 1>
// 2、在,则查找到的节点中水果对应的次数++
//BSTreeNode<string, int>* ret = countTree.Find(str);
auto ret = countTree.Find(str);
if (ret == NULL)
{
countTree.Insert(str , 1);
}
else
{
ret->_value++;
}
}
countTree.InOrder();
}
🎆🎆🎆来看效果🎆🎆🎆

🎆🎆🎆成功统计🎆🎆🎆
二叉搜索树还有许多应用场景,大家可以自行探索使用!!!