在计算机视觉和机器人领域,三维空间感知是实现环境理解和交互的核心技术之一。特别是在资源受限的场合,使用针孔模型的单目相机进行深度估计成为了一种既经济又实用的解决方案。单目深度估计技术依赖于从连续视频帧中提取和匹配特征点,以估计场景中物体的三维位置。本文将探讨几种基于单目相机前后帧特征点匹配的3D深度估计方法。通过详细分析特征点匹配及其对深度恢复的贡献,我们旨在提供一种既精确又实用的深度估计技术,适用于从自动驾驶到增强现实等多种应用场景。

一、通过多视角立体几何 (Multi-view Stereo, MVS)的方法
1. 原理
特征点三角化是VSLAM中的一个基础问题,用于根据特征点在多个相机中的投影来恢复其在3D坐标中的位置。其的基本思想是:在某个相机中观测到的特征点可以通过相机位姿和观测向量来确定一条从相机中心出发的观测射线。当存在多个相机位姿观测时,会生成多条观测射线。理想情况下,这些观测射线会在空间中的一个点相交。通过求解所有观测射线的交点,可以确定特征点在3D空间中的位置。

然而,在实际应用中,由于存在噪声,观测射线往往不会精确交于一点。为了确定特征点的坐标,有以下几种思路:
-
直观方法:寻找一个与所有观测射线距离都很近的三维点,将其作为特征点。
-
重投影误差最小化:认为误差源于二维图像观测,因此将特征点投影到每个相机平面,最小化所有二维投影点与对应观测点之间的距离(特征点的线性三角化(Triangulation)方法)。
-
在线滤波:三角化常常是在线进行的,即边获取观测边估计特征点。利用滤波器估计特征点的概率分布(通常为高斯分布),旧观测信息隐式存储在概率分布中。当新观测到来时,用其更新特征点的概率分布,节省计算量。这是滤波方法的基本思想。
设3D特征点被
个相机观测到,已知:相机姿态
,相机内参
,特征点在各相机的图像观测
,求:特征点的3D坐标
:
不考虑误差的情况有如下投影关系:
通过多视角立体几何 (Multi-view Stereo, MVS)的这类方法中,重点介绍思路2:重投影误差最小化。
设特征点齐次坐标,在第
个相机的图像观测点齐次坐标为
投影矩阵为
,投影模型如下:
由可得
,将其展开:
所以只有两个线性无关的方程,每个相机观测有两个线性方程,将个相机观测的约束方程合并得到
个线性方程:
这里可以使用SVD求解,齐次坐标即为
的最小奇异值的奇异向量。
2. 代码
代码来自:
orbslam2_learn/linear_triangular at master · yepeichu123/orbslam2_learn · GitHub![]() https://github.com/yepeichu123/orbslam2_learn/tree/master/linear_triangular
https://github.com/yepeichu123/orbslam2_learn/tree/master/linear_triangular
这里给代码添加了中文注释。
main.cpp
#include "linear_triangular.h"
// c++
#include <iostream>
#include <vector>
// opencv
#include <opencv2/calib3d/calib3d.hpp>
// pcl
#include <pcl-1.8/pcl/io/pcd_io.h>
#include <pcl-1.8/pcl/point_types.h>
#include <pcl-1.8/pcl/point_cloud.h>
#include <pcl-1.8/pcl/common/impl/io.hpp>
#include <pcl-1.8/pcl/visualization/cloud_viewer.h>
using namespace cv;
using namespace std;
using namespace pcl;
// 从图像中提取 ORB 特征并计算描述子
void featureExtraction( const Mat& img, vector<KeyPoint>& kpt, Mat& desp );
// 通过暴力匹配方法进行特征匹配
// 根据匹配得分的阈值选择一些良好的匹配对
void featureMatching( const Mat& rDesp, const Mat& cDesp, vector<DMatch>& matches,
const vector<KeyPoint>& rKpt, const vector<KeyPoint>& cKpt,
vector<Point2d>& goodRKpt, vector<Point2d>& goodCKpt );
// 通过对极几何(Epipolar geometry)估计运动
bool motionEstimation( const vector<Point2d>& goodRKpt, const vector<Point2d>& goodCKpt,
const Mat& K, Mat& Rcr, Mat& tcr );
// 比较我们的方法和 OpenCV 的三角化误差
void triangularByOpencv( const vector<Point2d>& RKpt, const vector<Point2d>& CKpt,
const Mat& Trw, const Mat& Tcw, const Mat& K,
vector<Point2d>& nRKpt, vector<Point2d>& nCKpt,
vector<Point3d>& Pw3dCV );
int main( int argc, char** argv )
{
// 确保我们有正确的输入数据
if( argc < 3 )
{
cout << "Please enter ./linear_triangular currImg refImg" << endl;
return -1;
}
// 从输入路径读取图像
Mat currImg = imread( argv[1], 1 );
Mat refImg = imread( argv[2], 1 );
// 根据数据集设置相机参数
Mat K = ( Mat_<double>(3,3) << 517.3, 0, 318.6, 0, 516.5, 255.3, 0, 0, 1 );
// 检测 ORB 特征并计算 ORB 描述子
vector<KeyPoint> ckpt, rkpt;
Mat cdesp, rdesp;
featureExtraction( currImg, ckpt, cdesp );
featureExtraction( refImg, rkpt, rdesp );
cout << "finish feature extration!" << endl;
// 特征匹配
vector<DMatch> matches;
vector<Point2d> goodCKpt, goodRKpt;
featureMatching( rdesp, cdesp, matches, rkpt, ckpt, goodRKpt, goodCKpt );
cout << "finish feature matching!" << endl;
// 运动估计
Mat Rcr, tcr;
if( !motionEstimation(goodRKpt, goodCKpt, K, Rcr, tcr) )
{
return -1;
}
cout << "finish motion estimation!" << endl;
// 构造变换矩阵
Mat Trw = Mat::eye(4,4,CV_64F);
Mat Tcr = (Mat_<double>(3,4) << Rcr.at<double>(0,0), Rcr.at<double>(0,1), Rcr.at<double>(0,2), tcr.at<double>(0),
Rcr.at<double>(1,0), Rcr.at<double>(1,1), Rcr.at<double>(1,2), tcr.at<double>(1),
Rcr.at<double>(2,0), Rcr.at<double>(2,1), Rcr.at<double>(2,2), tcr.at<double>(2),
0, 0, 0, 1);
// 传播变换
Mat Tcw = Tcr * Trw;
Trw = Trw.rowRange(0,3).clone();
Tcw = Tcw.rowRange(0,3).clone();
cout << "Tcw = " << Tcw << endl;
cout << "Trw = " << Trw << endl;
cout << "现在我们通过线性三角化来三角化匹配对。" << endl;
// 根据我们的博客开始三角化
vector<Point3d> Pw3d;
vector<Point2d> Pr2d;
XIAOC::LinearTriangular myTriangular( K, Trw, Tcw );
for( int i = 0; i < matches.size(); ++i )
{
Point3d pw;
bool result = myTriangular.TriangularPoint( goodRKpt[i], goodCKpt[i], pw );
// 检查三角化是否成功
if( !result )
{
continue;
}
//cout << "pw in world coordinate is " << pw << endl;
// 保存世界坐标系下的 3D 点
Pw3d.push_back( pw );
Pr2d.push_back( goodRKpt[i] );
}
// 根据 OpenCV 进行三角化
vector<Point3d> Pw3dCV;
vector<Point2d> nRKpt, nCKpt;
triangularByOpencv( goodRKpt, goodCKpt, Trw, Tcw, K, nRKpt, nCKpt, Pw3dCV);
// 重投影误差
double errorOurs = 0, errorOpencv = 0;
for( int i = 0; i < Pw3dCV.size(); ++i )
{
// 我们的三角化结果
Point3d Pw = Pw3d[i];
Point2d ppc = Point2d( Pw.x/Pw.z,Pw.y/Pw.z );
// OpenCV 的三角化结果
Point3d Pcv = Pw3dCV[i];
Point2d ppcv = Point2d( Pcv.x/Pcv.z, Pcv.y/Pcv.z );
// 参考归一化平面上的特征坐标
Point2d ppr = nRKpt[i];
errorOurs += norm( ppc - ppr );
errorOpencv += norm( ppcv - ppr );
}
cout << "我们的总误差是 " << errorOurs << endl;
cout << "OpenCV 的总误差是 " << errorOpencv << endl;
cout << "我们的平均误差是 " << errorOurs / Pw3d.size() << endl;
cout << "OpenCV 的平均误差是 " << errorOpencv / Pw3dCV.size() << endl;
// 显示关键点
Mat currOut;
drawKeypoints( currImg, ckpt, currOut, Scalar::all(-1), DrawMatchesFlags::DRAW_RICH_KEYPOINTS );
imshow( "CurrOut", currOut );
waitKey(0);
// 显示良好的匹配结果
Mat goodMatchOut;
drawMatches( refImg, rkpt, currImg, ckpt, matches, goodMatchOut );
imshow( "goodMatchOut", goodMatchOut );
waitKey(0);
// 将 3D 点转换为点云进行显示
PointCloud<PointXYZRGB>::Ptr cloud( new PointCloud<PointXYZRGB> );
for( int i = 0; i < Pw3d.size(); ++i )
{
PointXYZRGB point;
Point3d p = Pw3d[i];
Point2d pixel = Pr2d[i];
point.x = p.x;
point.y = p.y;
point.z = p.z;
point.r = refImg.at<Vec3b>(pixel.y,pixel.x)[0];
point.g = refImg.at<Vec3b>(pixel.y,pixel.x)[1];
point.b = refImg.at<Vec3b>(pixel.y,pixel.x)[2];
cloud->push_back( point );
}
cout << "点云的数量是 " << cloud->size() << endl;
visualization::CloudViewer viewer( "Viewer" );
viewer.showCloud( cloud );
while( !viewer.wasStopped() )
{
// loop loop loop~~~
}
cout << "成功!" << endl;
return 0;
}
// 特征提取并计算描述子
void featureExtraction( const Mat& img, vector<KeyPoint>& kpt, Mat& desp )
{
// 设置要提取的特征数量
Ptr<FeatureDetector> detector = ORB::create( 10000 );
Ptr<DescriptorExtractor> descriptor = ORB::create();
detector->detect( img, kpt );
descriptor->compute( img, kpt, desp );
}
// 通过暴力匹配方法进行特征匹配并找到良好的匹配
void featureMatching( const Mat& rDesp, const Mat& cDesp, vector<DMatch>& matches,
const vector<KeyPoint>& rKpt, const vector<KeyPoint>& cKpt,
vector<Point2d>& goodRKpt, vector<Point2d>& goodCKpt )
{
// 通过暴力匹配方法进行粗匹配,以汉明距离为度量
Ptr<DescriptorMatcher> matcher = DescriptorMatcher::create( "BruteForce-Hamming" );
vector<DMatch> initMatches;
matcher->match( rDesp, cDesp, initMatches );
cout << "初始匹配完成!" << endl;
// 计算最大距离和最小距离
double min_dist = min_element( initMatches.begin(), initMatches.end(),
[](const DMatch& m1, const DMatch& m2) {return m1.distance<m2.distance;} )->distance;
double max_dist = max_element( initMatches.begin(), initMatches.end(),
[](const DMatch& m1, const DMatch& m2) {return m1.distance<m2.distance;} )->distance;
// 找到良好的匹配并记录相应的像素坐标
for( int i = 0; i < initMatches.size(); ++i )
{
if( initMatches[i].distance <= max(min_dist*2, 30.0) )
{
matches.push_back( initMatches[i] );
goodRKpt.push_back( rKpt[initMatches[i].queryIdx].pt );
goodCKpt.push_back( cKpt[initMatches[i].trainIdx].pt );
}
}
}
// 估计当前帧和参考帧之间的运动
bool motionEstimation( const vector<Point2d>& goodRKpt, const vector<Point2d>& goodCKpt,
const Mat& K, Mat& Rcr, Mat& tcr )
{
// 根据对极几何计算本质矩阵
Mat E = findEssentialMat( goodRKpt, goodCKpt, K, RANSAC );
// 从本质矩阵恢复姿态
int inliers = recoverPose( E, goodRKpt, goodCKpt, K, Rcr, tcr );
// 确保我们有足够的内点进行三角化
return inliers > 100;
}
// 比较我们的方法和 OpenCV 的三角化误差
void triangularByOpencv( const vector<Point2d>& RKpt, const vector<Point2d>& CKpt,
const Mat& Trw, const Mat& Tcw, const Mat& K,
vector<Point2d>& nRKpt, vector<Point2d>& nCKpt,
vector<Point3d>& Pw3dCV )
{
Mat pts_4d;
// 将特征点反投影到归一化平面
for( int i = 0; i < RKpt.size(); ++i )
{
Point2d pr( (RKpt[i].x-K.at<double>(0,2))/K.at<double>(0,0),
(RKpt[i].y-K.at<double>(1,2))/K.at<double>(1,1) );
Point2d pc( (CKpt[i].x-K.at<double>(0,2))/K.at<double>(0,0),
(CKpt[i].y-K.at<double>(1,2))/K.at<double>(1,1) );
nRKpt.push_back( pr );
nCKpt.push_back( pc );
}
// 三角化点
triangulatePoints( Trw, Tcw, nRKpt, nCKpt, pts_4d );
// 从齐次坐标中恢复位置
for( int i = 0; i < pts_4d.cols; ++i )
{
Mat x = pts_4d.col(i);
x /= x.at<double>(3,0);
Point3d pcv( x.at<double>(0,0), x.at<double>(1,0), x.at<double>(2,0));
Pw3dCV.push_back( pcv );
}
cout << "pw3d 的大小 = " << Pw3dCV.size() << endl;
}liner_triangular.cpp
#include "linear_triangular.h"
#include <iostream>
// 构造函数:设置相机参数和变换矩阵
XIAOC::LinearTriangular::LinearTriangular(const cv::Mat& K, const cv::Mat& Trw, const cv::Mat& Tcw):
mK_(K), mTrw_(Trw), mTcw_(Tcw)
{
}
// 从两个视图的特征点三角化出 3D 点
// 输入:2D pr 和 2D pc,分别是参考帧和当前帧中的像素坐标
// 输出:3D Pw,即世界坐标系下的 3D 坐标
bool XIAOC::LinearTriangular::TriangularPoint(const cv::Point2d& pr, const cv::Point2d& pc, cv::Point3d& Pw )
{
// 反投影到归一化平面
UnprojectPixel( pr, pc );
// 构造矩阵 A
ConstructMatrixA( mPrn_, mPcn_, mTrw_, mTcw_ );
// 获取 3D 位置
if( CompBySVD( mA_, mPw_ ) )
{
Pw = mPw_;
return true;
}
return false;
}
// 将像素点反投影到归一化平面
void XIAOC::LinearTriangular::UnprojectPixel(const cv::Point2d& pr, const cv::Point2d& pc)
{
// X = (u-cx)/fx;
// Y = (v-cy)/fy;
mPrn_.x = (pr.x - mK_.at<double>(0,2))/mK_.at<double>(0,0);
mPrn_.y = (pr.y - mK_.at<double>(1,2))/mK_.at<double>(1,1);
mPrn_.z = 1;
mPcn_.x = (pc.x - mK_.at<double>(0,2))/mK_.at<double>(0,0);
mPcn_.y = (pc.y - mK_.at<double>(1,2))/mK_.at<double>(1,1);
mPcn_.z = 1;
}
// 根据我们的博客构造矩阵 A
void XIAOC::LinearTriangular::ConstructMatrixA(const cv::Point3d& Prn, const cv::Point3d& Pcn, const cv::Mat& Trw, const cv::Mat& Tcw )
{
// ORBSLAM 方法
/* cv::Mat A(4,4,CV_64F);
A.row(0) = Prn.x*Trw.row(2)-Trw.row(0);
A.row(1) = Prn.y*Trw.row(2)-Trw.row(1);
A.row(2) = Pcn.x*Tcw.row(2)-Tcw.row(0);
A.row(3) = Pcn.y*Tcw.row(2)-Tcw.row(1);
A.copyTo( mA_ );
*/
// 我博客中的原始方法
cv::Mat PrnX = (cv::Mat_<double>(3,3) << 0, -Prn.z, Prn.y,
Prn.z, 0, -Prn.x,
-Prn.y, Prn.x, 0);
cv::Mat PcnX = (cv::Mat_<double>(3,3) << 0, -Pcn.z, Pcn.y,
Pcn.z, 0, -Pcn.x,
-Pcn.y, Pcn.x, 0);
// A = [prX*Trw; pcX*Tcw ]
// APw = 0
cv::Mat B = PrnX * Trw;
cv::Mat C = PcnX * Tcw;
cv::vconcat( B, C, mA_ );
}
// 通过计算 SVD 求解问题
bool XIAOC::LinearTriangular::CompBySVD(const cv::Mat& A, cv::Point3d& Pw )
{
if( A.empty() )
{
return false;
}
// 计算矩阵 A 的 SVD
cv::Mat w, u, vt;
cv::SVD::compute( A, w, u, vt, cv::SVD::MODIFY_A|cv::SVD::FULL_UV );
// 归一化
cv::Mat Pw3d;
Pw3d = vt.row(3).t();
if( Pw3d.at<double>(3) == 0 )
{
return false;
}
Pw3d = Pw3d.rowRange(0,3)/Pw3d.at<double>(3);
// 保存位置的值
Pw.x = Pw3d.at<double>(0);
Pw.y = Pw3d.at<double>(1);
Pw.z = Pw3d.at<double>(2);
return true;
}
// 检查两个视图之间特征点的角度
bool XIAOC::LinearTriangular::CheckCrossAngle( const cv::Point3d& Prn, const cv::Point3d& Pcn,
const cv::Mat& Trw, const cv::Mat& Tcw )
{
// 待办:通过角度检查是否适合三角化
}
// 检查我们三角化得到的点的深度是否正确
bool XIAOC::LinearTriangular::CheckDepth( const cv::Point3d& Pw3d )
{
// 待办:通过深度检查是否适合接受
}
CMakeList.txt
cmake_minimum_required( VERSION 2.8 )
project( linear_triangular )
set( CMAKE_BUILD_TYPE "Release" )
set( CMAKE_CXX_FLAGS "-std=c++11" )
set( EXECUTABLE_OUTPUT_PATH ${PROJECT_SOURCE_DIR}/bin )
set( LIBRARY_OUTPUT_PATH ${PROJECT_SOURCE_DIR}/lib )
find_package( OpenCV 3.0 REQUIRED )
include_directories( ${OpenCV_INCLUDE_DIRS} )
find_package( PCL REQUIRED )
include_directories( ${PCL_INCLUDE_DIRS} )
link_directories( ${PCL_LIBRARY_DIRS} )
add_definitions( ${PCL_DEFINITIONS} )
include_directories( ${PROJECT_SOURCE_DIR}/include )
#add_subdirectory( ${PROJECT_SOURCE_DIR} )
add_executable( linear_triangular src/linear_triangular.cpp src/main.cpp )
target_link_libraries( linear_triangular ${OpenCV_LIBS} ${PCL_LIBRARIES} )
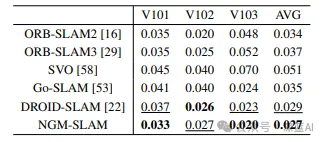
3. 结果



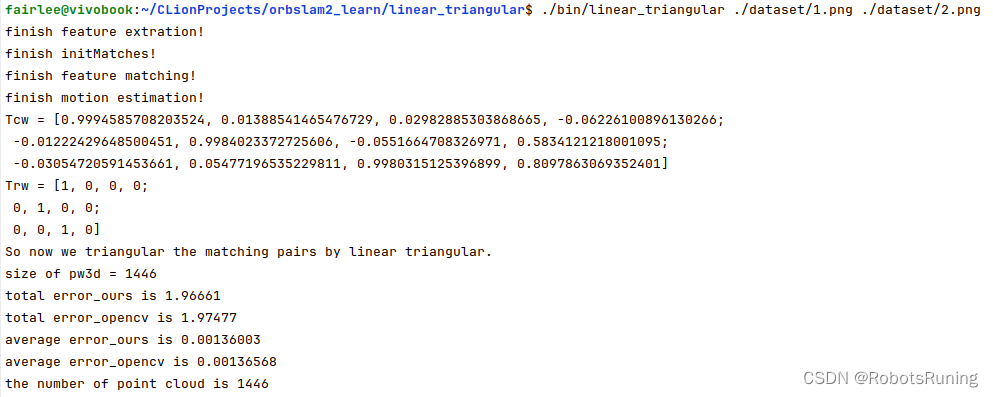
二、通过端到端深度学习方法估计单目深度---DPT
Ranftl et al. (2020) - 提出了一种基于Transformer的深度估计方法,称为Vision Transformer for Dense Prediction (DPT)。该方法利用了Transformer强大的全局建模能力,通过self-attention机制学习像素之间的长距离依赖关系。同时,他们还设计了一种多尺度融合策略,以结合不同层次的特征信息。DPT在多个数据集上都取得了最先进的性能。
1. 原理
根据论文 "Vision Transformers for Dense Prediction" 的内容,Dense Prediction Transformers (DPT) 的主要原理可以总结如下:DPT在编码器-解码器架构中利用视觉transformer (ViT)作为骨干网络,用于深度估计和语义分割等密集预测任务。与逐步下采样特征图的卷积骨干网络不同,ViT骨干网络通过对分块/令牌进行操作,在整个过程中保持恒定的空间分辨率。在每个阶段,ViT通过自注意力机制具有全局感受野。这允许在高分辨率下捕获长距离依赖关系。来自不同ViT阶段的令牌被重组为多尺度的类图像特征。然后,卷积解码器融合这些特征并对其进行上采样,以获得最终的密集预测。通过在每个阶段保持高分辨率并具有全局感受野,与全卷积网络相比,DPT能够提供细粒度和全局连贯的预测。当有大量训练数据可用时,DPT在先前技术的基础上大幅改进,在具有挑战性的数据集上设置了新的最先进水平。
总之,DPT的创新之处在于使用了ViT骨干,该骨干在每个阶段以全局上下文处理高分辨率特征,然后由卷积解码器将其合并为细粒度预测,从而在密集预测任务上显著提高了性能。(不是搞深度学习的我也看不懂啊,读者自行分别吧。这个坑后面再填)
2. 代码
代码连接: https://github.com/intel-isl/DPT![]() https://github.com/intel-isl/DPT论文连接:
https://github.com/intel-isl/DPT论文连接:
https://arxiv.org/pdf/2103.13413![]() https://arxiv.org/pdf/2103.13413
https://arxiv.org/pdf/2103.13413
3. 结果

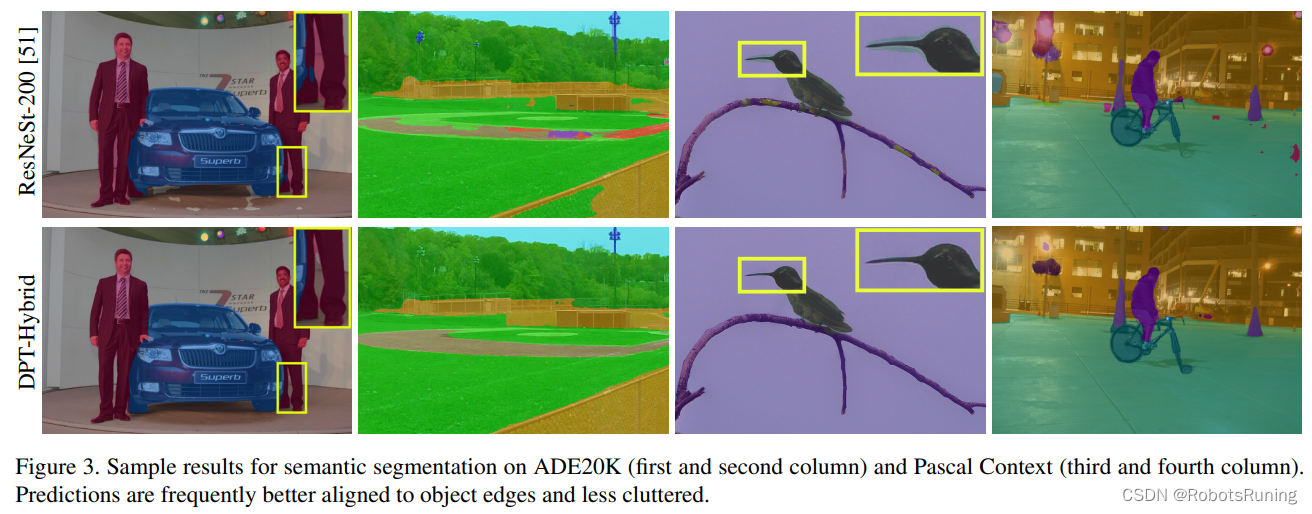
参考文章:
VSLAM中的特征点三角化 - 知乎 (zhihu.com)
SLAM--三角化求解3D空间点_jacobisvd(eigen::computefullv).matrixv()-CSDN博客