目录
- 第二门课: 改善深层神经网络:超参数调试、正 则 化 以 及 优 化 (Improving Deep Neural Networks:Hyperparameter tuning, Regularization and Optimization)
- 第二周:优化算法 (Optimization algorithms)
- 2.7 RMSprop
第二门课: 改善深层神经网络:超参数调试、正 则 化 以 及 优 化 (Improving Deep Neural Networks:Hyperparameter tuning, Regularization and Optimization)
第二周:优化算法 (Optimization algorithms)
2.7 RMSprop
你们知道了动量(Momentum)可以加快梯度下降,还有一个叫做 RMSprop 的算法,全称是 root mean square prop 算法,它也可以加速梯度下降,我们来看看它是如何运作的。
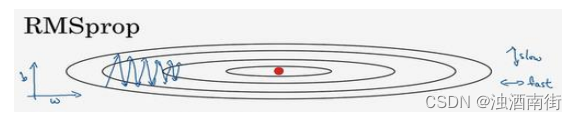
回忆一下我们之前的例子,如果你执行梯度下降,虽然横轴方向正在推进,但纵轴方向会有大幅度摆动,为了分析这个例子,假设纵轴代表参数𝑏,横轴代表参数𝑊,可能有𝑊1,𝑊2或者其它重要的参数,为了便于理解,被称为𝑏和𝑊。
所以,你想减缓𝑏方向的学习,即纵轴方向,同时加快,至少不是减缓横轴方向的学习,RMSprop 算法可以实现这一点。
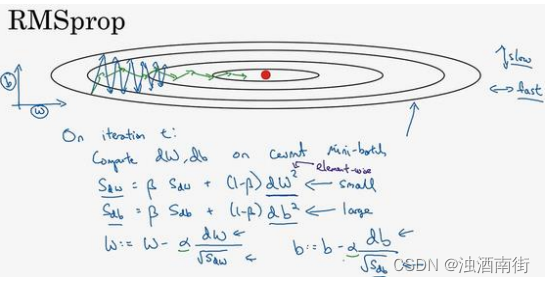
在第𝑡次迭代中,该算法会照常计算当下 mini-batch 的微分dW,db,所以我会保留这个指数加权平均数,我们用到新符号
S
d
W
S_{dW}
SdW,而不是
v
d
W
v_{dW}
vdW,因此
S
d
W
=
β
S
d
W
+
(
1
−
β
)
d
W
2
S_{dW} = βS_{dW} + (1 − β)dW^2
SdW=βSdW+(1−β)dW2,澄清一下,这个平方的操作是针对这一整个符号的,这样做能够保留微分平方的加权平均数,同样
S
d
b
=
β
S
d
b
+
(
1
−
β
)
d
b
2
S_{db} = βS_{db} + (1 − β)db^2
Sdb=βSdb+(1−β)db2,再说一次,平方是针对整个符号的操作。
接着 RMSprop 会这样更新参数值:
W : = W − α d W S d W , b : = b − α d b S d b W: = W − \alpha \frac {dW}{\sqrt {S_{dW}}},b: = b − \alpha \frac{db}{\sqrt {S_{db}}} W:=W−αSdWdW,b:=b−αSdbdb
我们来理解一下其原理。记得在横轴方向或者在例子中的𝑊方向,我们希望学习速度快,而在垂直方向,也就是例子中的𝑏方向,我们希望减缓纵轴上的摆动,所以有了 S d W S_{dW} SdW和 S d b S_{db} Sdb,我们希望 S d W S_{dW} SdW会相对较小,所以我们要除以一个较小的数,而希望 S d b S_{db} Sdb又较大,所以这里我们要除以较大的数字,这样就可以减缓纵轴上的变化。你看这些微分,垂直方向的要比水平方向的大得多,所以斜率在𝑏方向特别大,所以这些微分中,𝑑𝑏较大,𝑑𝑊较小,因为函数的倾斜程度,在纵轴上,也就是 b 方向上要大于在横轴上,也就是𝑊方向上。𝑑𝑏的平方较大,所以 S d b S_{db} Sdb也会较大,而相比之下,𝑑𝑊会小一些,亦或𝑑𝑊平方会小一些,因此 S d W S_{dW} SdW会小一些,结果就是纵轴上的更新要被一个较大的数相除,就能消除摆动,而水平方向的更新则被较小的数相除。
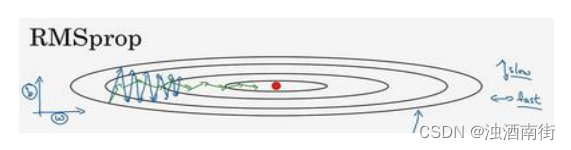
RMSprop 的影响就是你的更新最后会变成这样(绿色线),纵轴方向上摆动较小,而横轴方向继续推进。还有个影响就是,你可以用一个更大学习率𝑎,然后加快学习,而无须在纵轴上垂直方向偏离。
要说明一点,我一直把纵轴和横轴方向分别称为𝑏和𝑊,只是为了方便展示而已。实际中,你会处于参数的高维度空间,所以需要消除摆动的垂直维度,你需要消除摆动,实际上是参数 W 1 W_1 W1, W 2 W_2 W2等的合集,水平维度可能 W 3 W_3 W3, W 4 W_4 W4等等,因此把𝑊和𝑏分开只是方便说明。实际中𝑑𝑊是一个高维度的参数向量,𝑑𝑏也是一个高维度参数向量,但是你的直觉是,在你要消除摆动的维度中,最终你要计算一个更大的和值,这个平方和微分的加权平均值,所以你最后去掉了那些有摆动的方向。所以这就是 RMSprop,全称是均方根,因为你将微分进行平方,然后最后使用平方根。
最后再就这个算法说一些细节的东西,然后我们再继续。下一个视频中,我们会将RMSprop 和 Momentum 结合起来,我们在 Momentum 中采用超参数𝛽,为了避免混淆,我们现在不用𝛽,而采用超参数𝛽2以保证在 Momentum 和 RMSprop 中采用同一超参数。要确保你的算法不会除以 0,如果𝑆𝑑𝑊的平方根趋近于 0 怎么办?得到的答案就非常大,为了确保数值稳定,在实际操练的时候,你要在分母上加上一个很小很小的𝜀,𝜀是多少没关系, 1 0 − 8 10^{−8} 10−8是个不错的选择,这只是保证数值能稳定一些,无论什么原因,你都不会除以一个很小很小的数。所以 RMSprop 跟 Momentum 有很相似的一点,可以消除梯度下降中的摆动,包括mini-batch 梯度下降,并允许你使用一个更大的学习率 α \alpha α,从而加快你的算法学习速度。
所以你学会了如何运用 RMSprop,这是给学习算法加速的另一方法。关于 RMSprop 的一个有趣的事是,它首次提出并不是在学术研究论文中,而是在多年前Jeff Hinton在Coursera的课程上。我想 Coursera 并不是故意打算成为一个传播新兴的学术研究的平台,但是却达到了意想不到的效果。就是从 Coursera 课程开始,RMSprop 开始被人们广为熟知,并且发展迅猛。
我们讲过了 Momentum,我们讲了 RMSprop,如果二者结合起来,你会得到一个更好的优化算法,在下个视频中我们再好好讲一讲为什么。