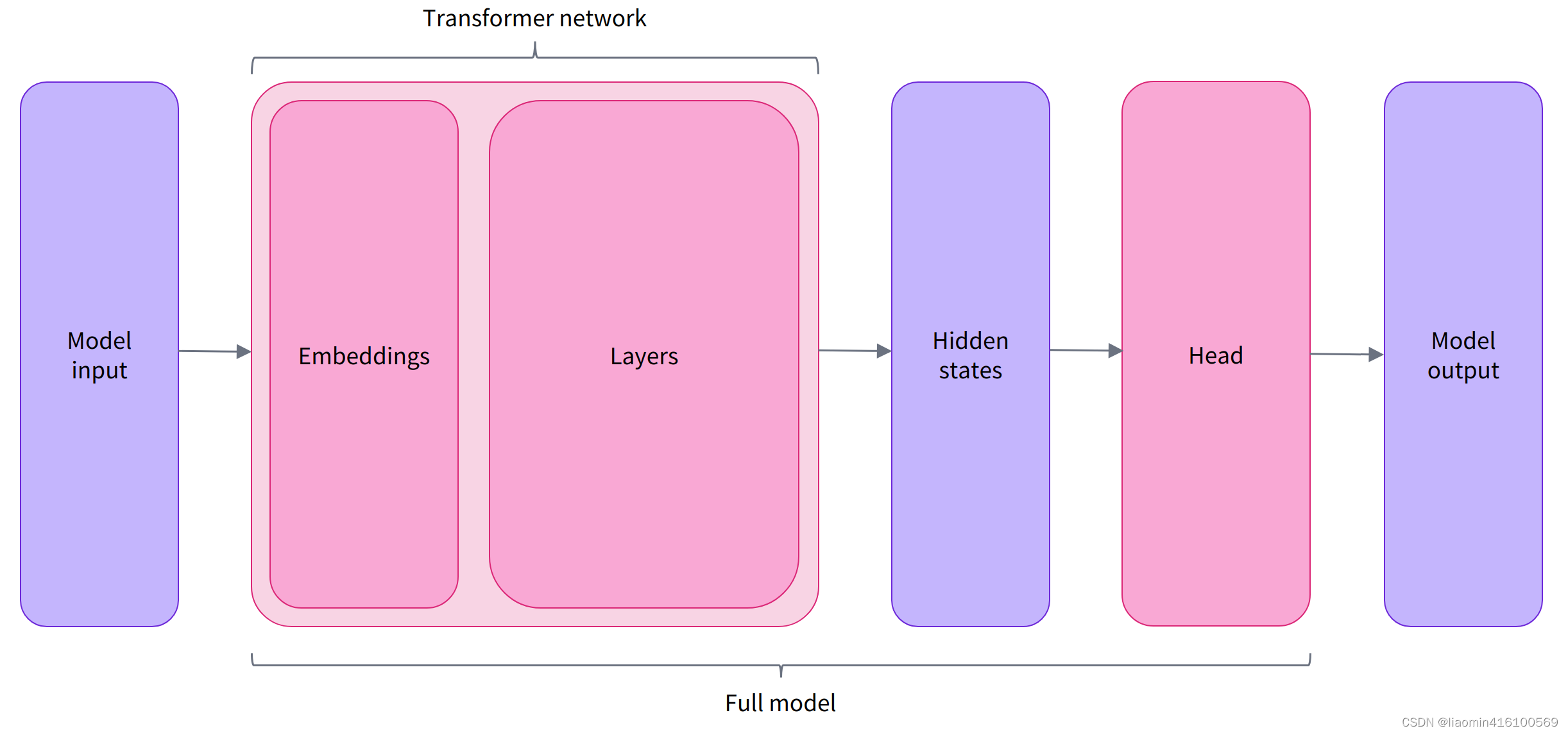
一、向量的加法运算
三角形法则(推荐)
两个或多个向量收尾相连的加法运算,用三角形法则

简便算法
首尾相连的多个向量,去掉中间点,就是最终的和。
也可以用三角形法则证明


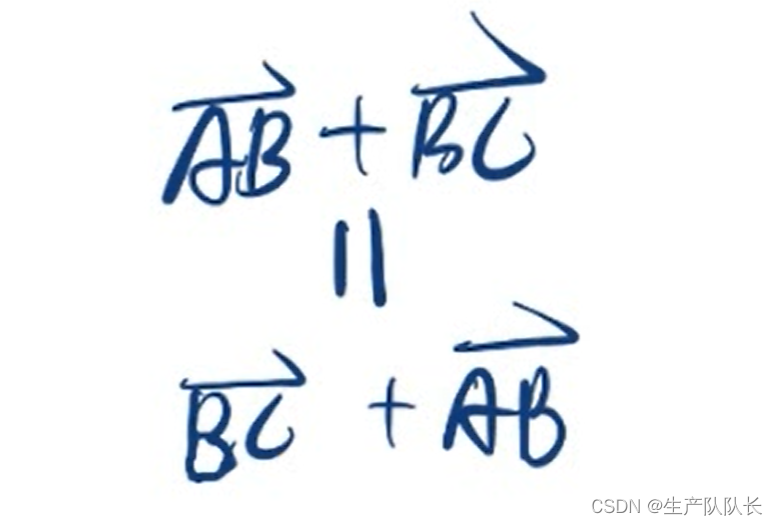
向量加法交换律
向量加法结合律
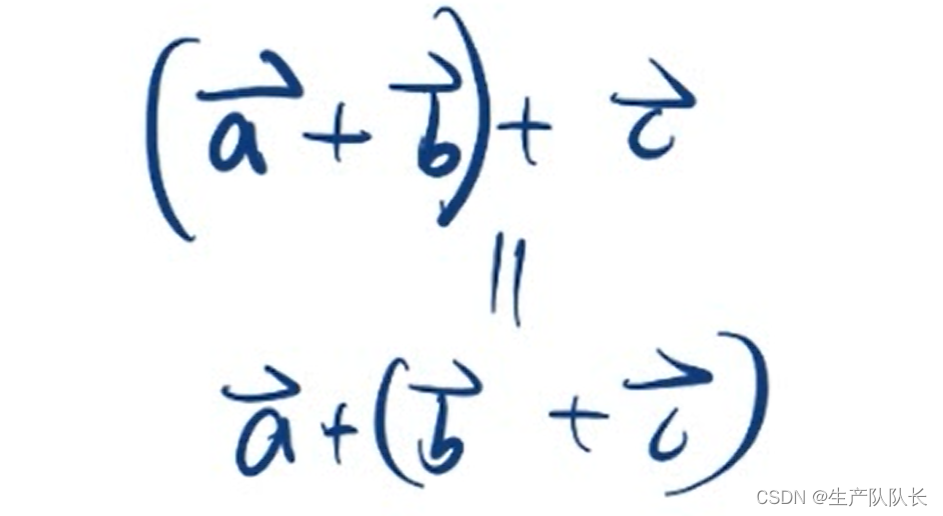
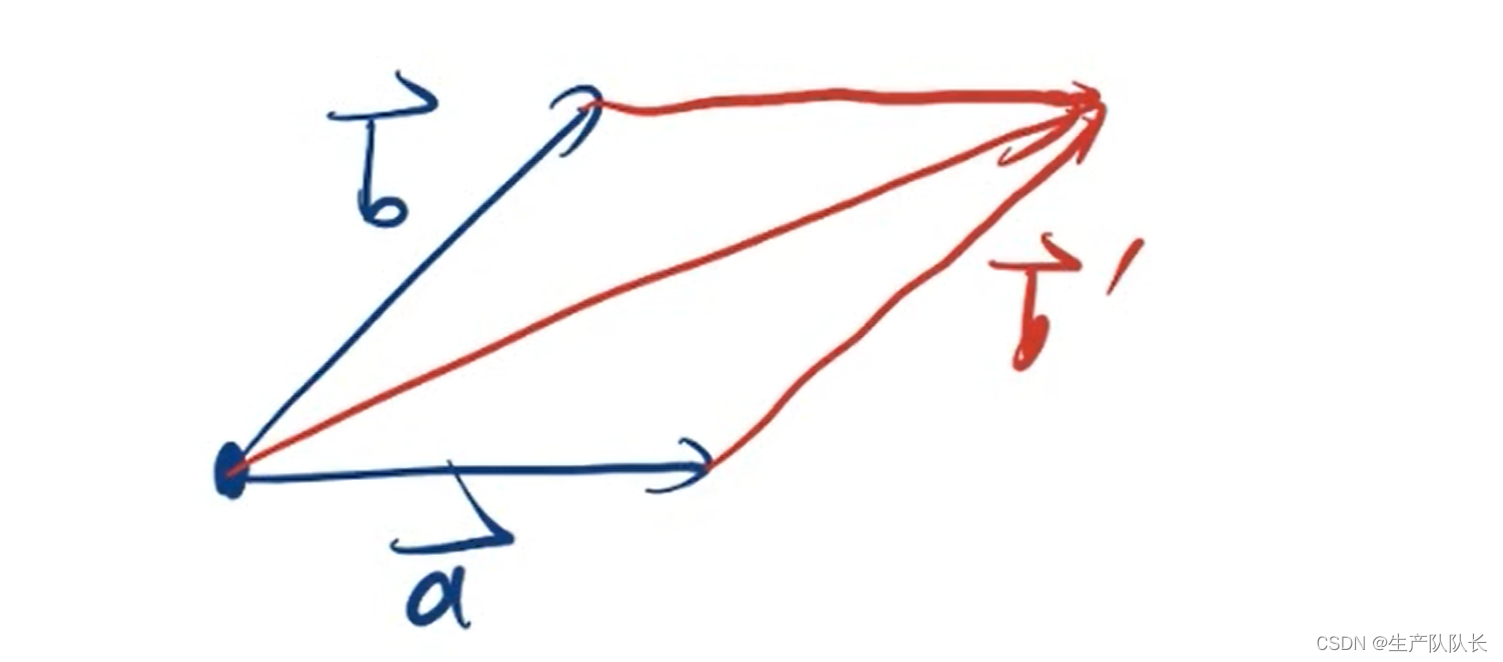
平行四边形法则
两个向量共同起点的时候,采用平行四边形法则
由于向量是可以平移的,所以,共同起点的向量,我们通过平移可以转化成首尾相连,从而可以采用三角形法则
特殊情况
同向与反向的两个向量相加

二、向量的减法运算
由于,向量的负向量,就是自身的反向量,大小相等,方向相反
有
a
→
\mathop{a}\limits ^{\rightarrow}
a→ + (
−
a
→
\mathop{-a}\limits ^{\rightarrow}
−a→ ) =
0
→
\mathop{0}\limits ^{\rightarrow}
0→
所以,减法运算可以转化成加法运算
即
a
→
\mathop{a}\limits ^{\rightarrow}
a→ -
b
→
\mathop{b}\limits ^{\rightarrow}
b→ =
a
→
\mathop{a}\limits ^{\rightarrow}
a→ + (
−
b
→
\mathop{-b}\limits ^{\rightarrow}
−b→)
其他,性质与加法运算相同
三、基本结论
零向量的加法运算
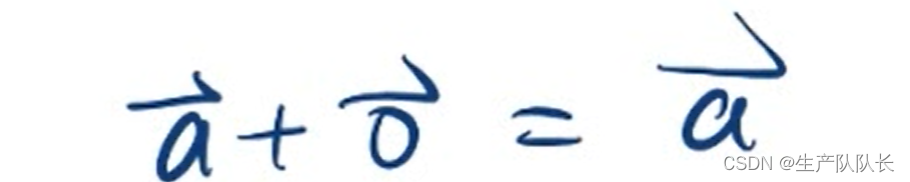
负向量
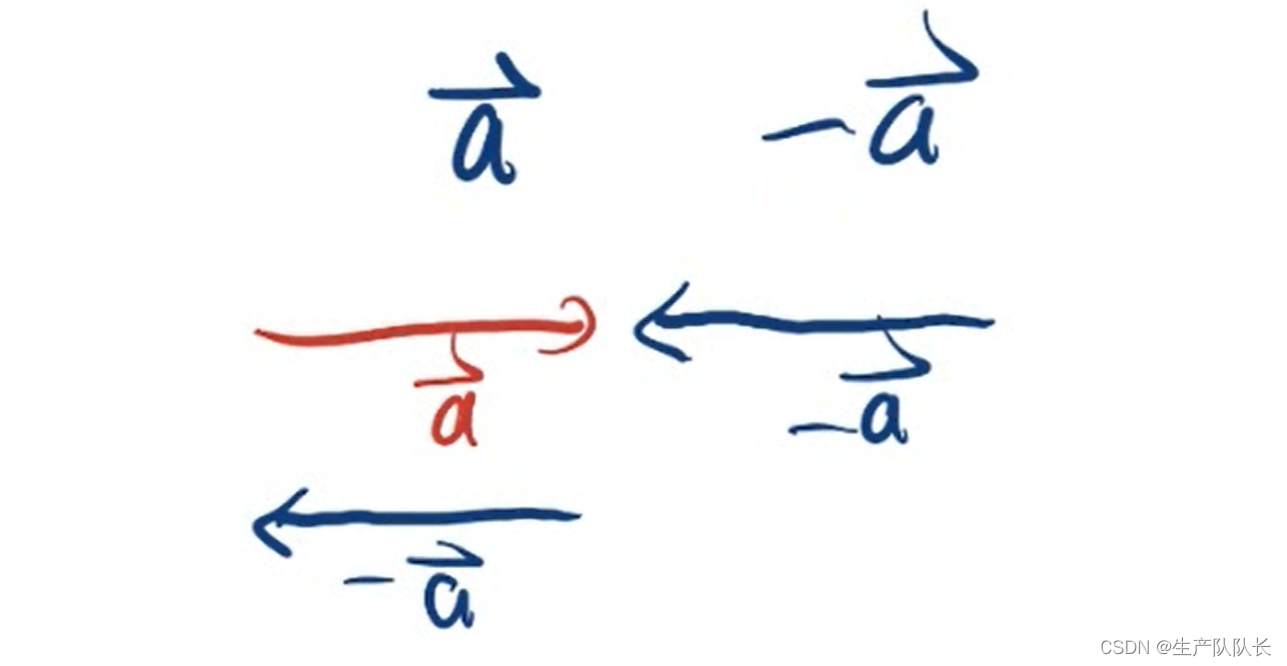
基本不等式

四、练习
例题1
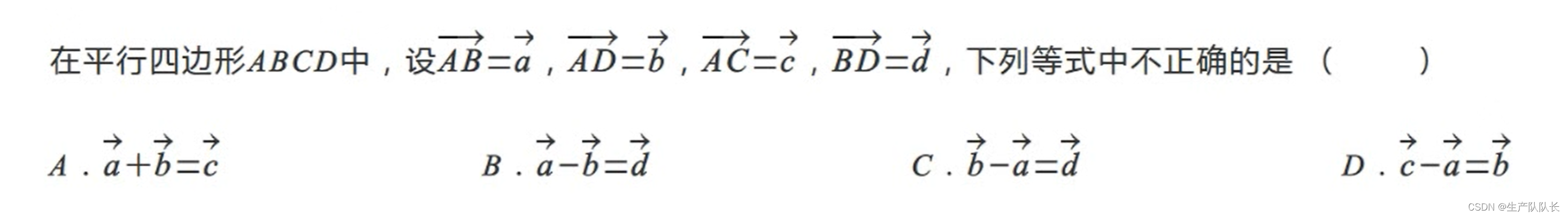
例题2
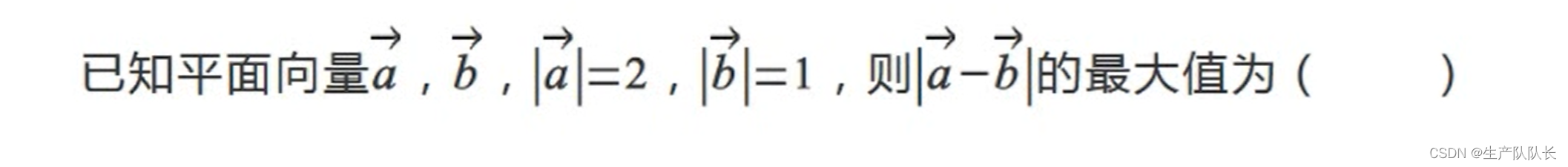
解析
这一题,用向量的基本不等式求直接秒杀
最大值,即
−
b
→
\mathop{-b}\limits ^{\rightarrow}
−b→ 与
a
→
\mathop{a}\limits ^{\rightarrow}
a→ 同向
最小值,即
−
b
→
\mathop{-b}\limits ^{\rightarrow}
−b→ 与
a
→
\mathop{a}\limits ^{\rightarrow}
a→ 反向