2024 National Invitational of CCPC (Zhengzhou)
2024CCPC郑州邀请赛暨CCPC河南省赛
2024 National Invitational of CCPC (Zhengzhou)

B. 扫雷 1
题意:扫n轮雷,每轮开始获得一枚扫雷币,可保存,从第一轮开始,可以决定在任意轮进行任意次扫雷,但过去的轮数不能返回,第i轮需要花费 c i c_i ci枚扫雷币扫雷一次,n轮最多扫多少雷。
思路:记录一个最便宜的扫雷后缀,遇见当前后缀最便宜的就开始买。
AC code:
void solve() {
int n; cin >> n;
for (int i = 1; i <= n; i ++) cin >> a[i];
r[n + 1] = INF;
for (int i = n; i >= 1; i --) {
r[i] = min(r[i + 1], a[i]);
}
int cnt = 0, now = 0;
for (int i = 1; i <= n; i ++) {
now ++;
if (a[i] == r[i]) {
cnt += now / a[i];
now -= (now / a[i]) * a[i];
}
}
cout << cnt << endl;
}
F. 优秀字符串
题意:略;
思路:照着题意模拟即可;
AC code:
void solve() {
int n; cin >> n;
int cnt = 0;
while (n --) {
string s; cin >> s;
if (s.size() != 5) continue;
if (s[2] != s[4]) continue;
bool flag = 1;
for (int i = 0; i < 4; i ++) for (int j = i + 1; j < 4; j ++) {
if (s[i] == s[j]) flag = 0;
}
if (flag) cnt ++;
}
cout << cnt << endl;
}
H. 随机栈
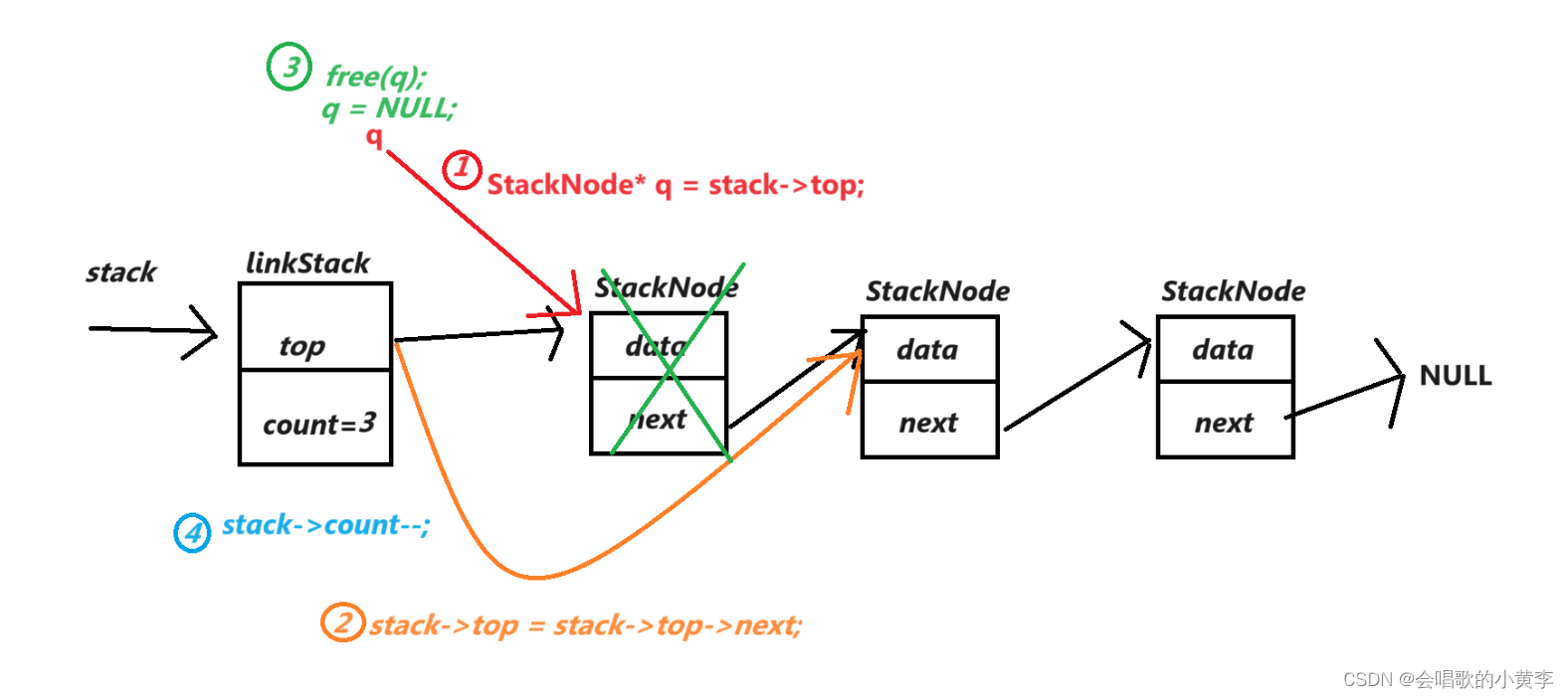
题意:给出一个空栈,还有一个操作序列,当当前操作元素不为-1时,将该元素压入栈中,否则取出一个栈中元素,取出当前栈中每个元素的概率是相同的,求最终取出元素序列为非递减的概率是多少,结果对998244353取模。
思路:模拟这个过程可以用优先队列来解决,当前栈中的元素总数为分母,当前队头的最小元素的数量即为分子,该数量可以用map来记录,计算不同分数的积并进行取模;
注意,运算过程中需要对各分数进行逆元取模运算,即分子*分母的逆元的过程不断累乘,过程中注意取模;
AC code:
int qmi(int a, int k, int p) {
int res = 1;
while (k) {
if (k & 1) res = res * a % p;
a = a * a % p;
k >>= 1;
} return res;
}
void solve() {
int n; cin >> n;
map<int, int> mp;
priority_queue<int, vector<int>, greater<int>> q;
int x = 1, y = 1;
int ans = qmi(1, MOD - 2, MOD);
for (int i = 1; i <= 2*n; i ++) {
cin >> a[i];
}
int last = -1;
for (int i = 1; i <= 2*n; i ++) {
if (a[i] == -1) {
int t = q.top();
if (last <= t) last = t;
else {
cout << 0 << endl;
return;
}
int xx = mp[t], yy = q.size();
int gd = gcd(xx, yy);
//cout << xx << ' ' << yy <<' ' << gd << endl;
ans = ((ans * xx) % MOD) * qmi(yy, MOD - 2, MOD) % MOD;
mp[t] --;
q.pop();
} else {
q.push(a[i]);
mp[a[i]] ++;
}
}
cout << ans % MOD << endl;
}
J. 排列与合数
题意:给出一个五位数字,重排后在没有前导零的情况下是否可能出现合数;
思路:预处理一下五位的合数,O1进行判断,然后DFS跑一下五位数的全排列即可;
AC code:
#include<bits/stdc++.h>
#define endl '\n'
#define int long long
#define fast() ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr)
using namespace std;
typedef long long LL;
typedef pair<int, int> PII;
const int N = 2e5+10, M = 2001;
const int INF = 0x3f3f3f3f3f, MOD = 998244353;
int T;
int n, ans;
int a[N], b[N], st[10];
bool p[N];
bool iprime(int x) {
if (x == 1) return false;
for (int i = 2; i <= x / i; i ++) {
if (x % i == 0) {
return true;
}
} return false;
}
void dfs(string aim, string s) {
if (ans != -1) return;
if (aim.size() == 5) {
int cnt = 0, tt = 10000;
if (aim[0] == '0') return;
for (int i = 0; i < 5; i ++) {
cnt += (aim[i] - '0') * tt;
tt /= 10;
}
if (p[cnt]) {
ans = cnt;
return;
}
return;
}
for (int i = 0; i < 5; i ++) {
if (!st[i]) {
st[i] = 1;
aim += s[i];
dfs(aim, s);
aim.pop_back();
st[i] = 0;
}
}
}
void solve() {
string s; cin >> s;
for (int i = 0; i < 5; i ++) st[i] = 0;
string ss = "";
ans = -1;
dfs(ss, s);
cout << ans << endl;
}
signed main() {
fast();
T = 1;
for (int i = 1; i < 100000; i ++) {
if (iprime(i)) p[i] = 1;
else p[i] = 0;
}
cin >> T;
while (T --) {
solve();
}
return 0;
}
K. 树上问题
题意:n个结点的无根树,每个结点有一个正权值,美丽节点的定义为,以当前节点为根时,除根节点外的所有节点,其点权不小于父节点的一半,计算有多少美丽节点。
思路:
首先初始就满足x * 2 >= y的节点y一定可以为x的父节点,即有一条有向边,若两个点互相可为父节点,则这两点可以由并查集记录为同一点在图中存在;
现在统计每个点当前可能的父节点,并根据上述情况合并到同一并查集中,记录每个连通块的大小;
然后通过DFS进行记录各点的出度,出度为0的点即为可能的根节点,注意在统计过程中进行标记防止重复统计;
注意,如果存在某一点的出度大于1,则该连通图必然不可能存在美丽节点。
AC code:
#include<bits/stdc++.h>
#define endl '\n'
#define int long long
#define fast() ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr)
using namespace std;
typedef long long LL;
typedef pair<int, int> PII;
const int N = 2e5+10, M = 2001;
const int INF = 0x3f3f3f3f3f, MOD = 998244353;
int T;
int n;
int a[N], f[N], d[N];
vector<int> g[N];
map<int, int> mp, pos;
int find(int x) {
if (f[x] != x) f[x] = find(f[x]);
return f[x];
}
void dfs(int u, int v) {
for (auto t : g[u]) {
if (t == v) continue;
dfs(t, u);
int fu = find(u), ft = find(t);
if (fu == ft) continue;
if (a[t] * 2 >= a[u] && a[u] * 2 >= a[t]) continue;
else if (a[t] * 2 >= a[u]) d[ft] ++;
else if (a[u] * 2 >= a[t]) d[fu] ++;
else d[ft] ++, d[fu] ++;
}
}
void solve() {
cin >> n;
mp.clear();
pos.clear();
for (int i = 1; i <= n; i ++) {
cin >> a[i];
f[i] = i;
d[i] = 0;
g[i].clear();
}
for (int i = 1; i < n; i ++) {
int u, v; cin >> u >> v;
g[u].push_back(v);
g[v].push_back(u);
int fu = find(u), fv = find(v);
if (a[u] * 2 >= a[v] && a[v] * 2 >= a[u]) {
f[f[u]] = fv;
}
}
for (int i = 1; i <= n; i ++) {
mp[find(i)] ++;
}
dfs(1, -1);
int ans = 0;
for (int i = 1; i <= n; i ++) {
if (d[find(i)] > 1) {
cout << 0 << endl;
return;
}
if (d[find(i)] || pos[find(i)]) continue;
pos[find(i)] ++;
ans += mp[find(i)];
}
cout << ans << endl;
}
signed main() {
fast();
T = 1;
cin >> T;
while (T --) {
solve();
}
return 0;
}
L. Toxel 与 PCPC II
题意:总共n行代码,已知m行有bug,扫描一行需要一秒,同时处理x个bug需要 x 4 x^4 x4秒,最短多少秒可以完成;
思路:dp,在更新每个点的最短debug时间时最多不会超过同时处理30个bug;
AC code:
int qmi (int a, int k) {
int res = 1;
while (k) {
if (k & 1) res = res * a;
a = a * a;
k >>= 1;
} return res;
}
void solve() {
int n, m; cin >> n >> m;
vector<int> a(m + 10), dp(m + 10, INF);
dp[0] = 0;
for (int i = 1; i <= m; i ++) cin >> a[i];
for (int i = 1; i <= m; i ++) {
for (int j = i - 1; j >= max(0LL, i - 30); j --) {
dp[i] = min(dp[i], dp[j] + a[i] + qmi(i - j, 4));
}
}
cout << dp[m] << endl;
}
M. 有效算法
题意:给出长度为n的序列a和b,对于每个a元素进行一次操作满足|ai - x| <= k * bi的任意整数x,求出最小的非负整数k,满足至少存在一种方法的操作后所有a元素相等
思路:二分即可,对于check函数每次x都会有一个左右边界,不断缩小左右边界,x只要出现在该范围内均符合条件,若出现r>l边界的情况则直接返回false,注意二分边界,最多开到1e9,不然会炸(血的教训)。
AC code:
bool check (int k) {
int l = -INF, r = INF;
for (int i = 1; i <= n; i ++) {
int now = k * b[i];
int ll = a[i] - now, rr = a[i] + now;
l = max(l, ll);
r = min(r, rr);
if (l > r) return false;
}
return true;
}
void solve() {
cin >> n;
for (int i = 1; i <= n; i ++) cin >> a[i];
for (int i = 1; i <= n; i ++) cin >> b[i];
int l = 0, r = 1e9;
while (l < r) {
int mid = l + r >> 1;
if (check(mid)) r = mid;
else l = mid + 1;
}
cout << r << endl;
}
PS:有没有佬有A的写法QAQ