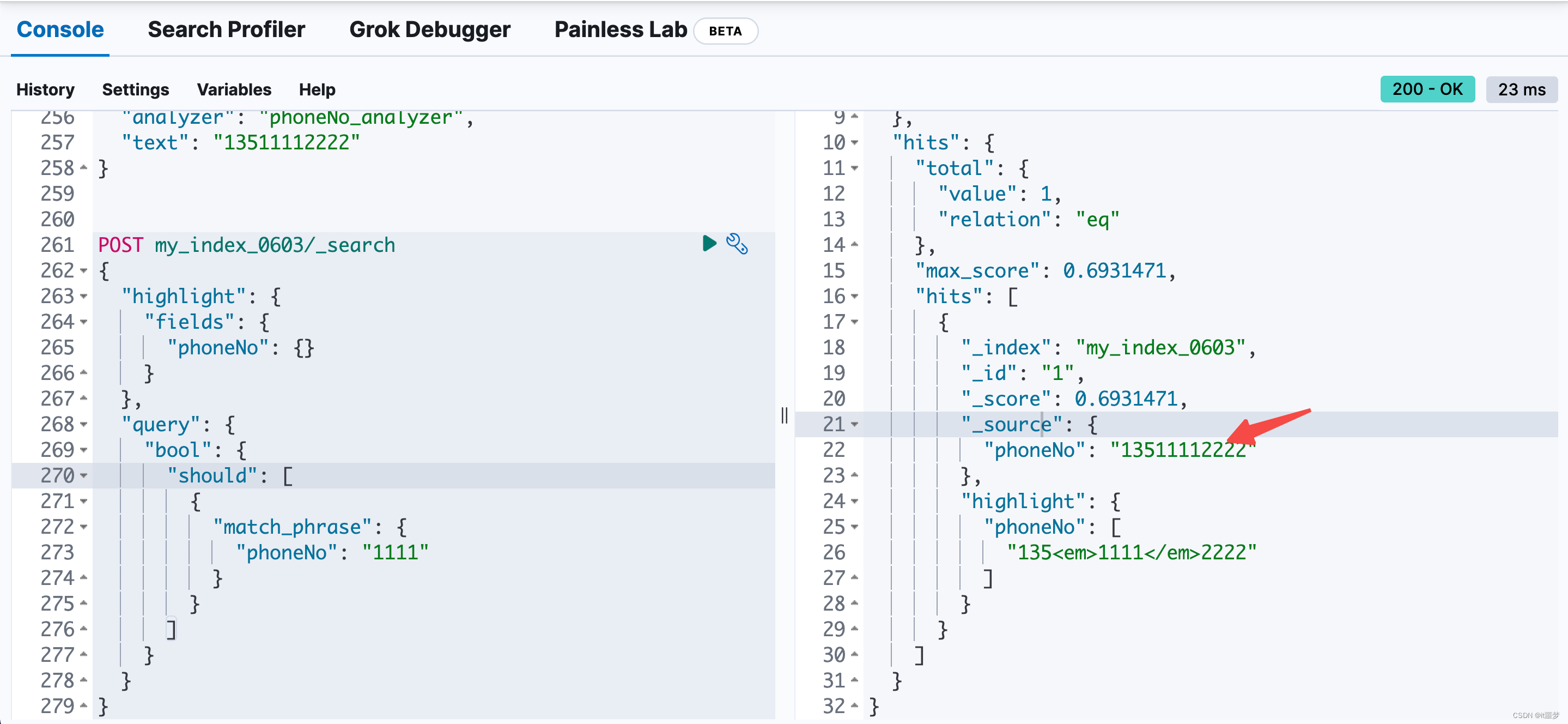
题干:
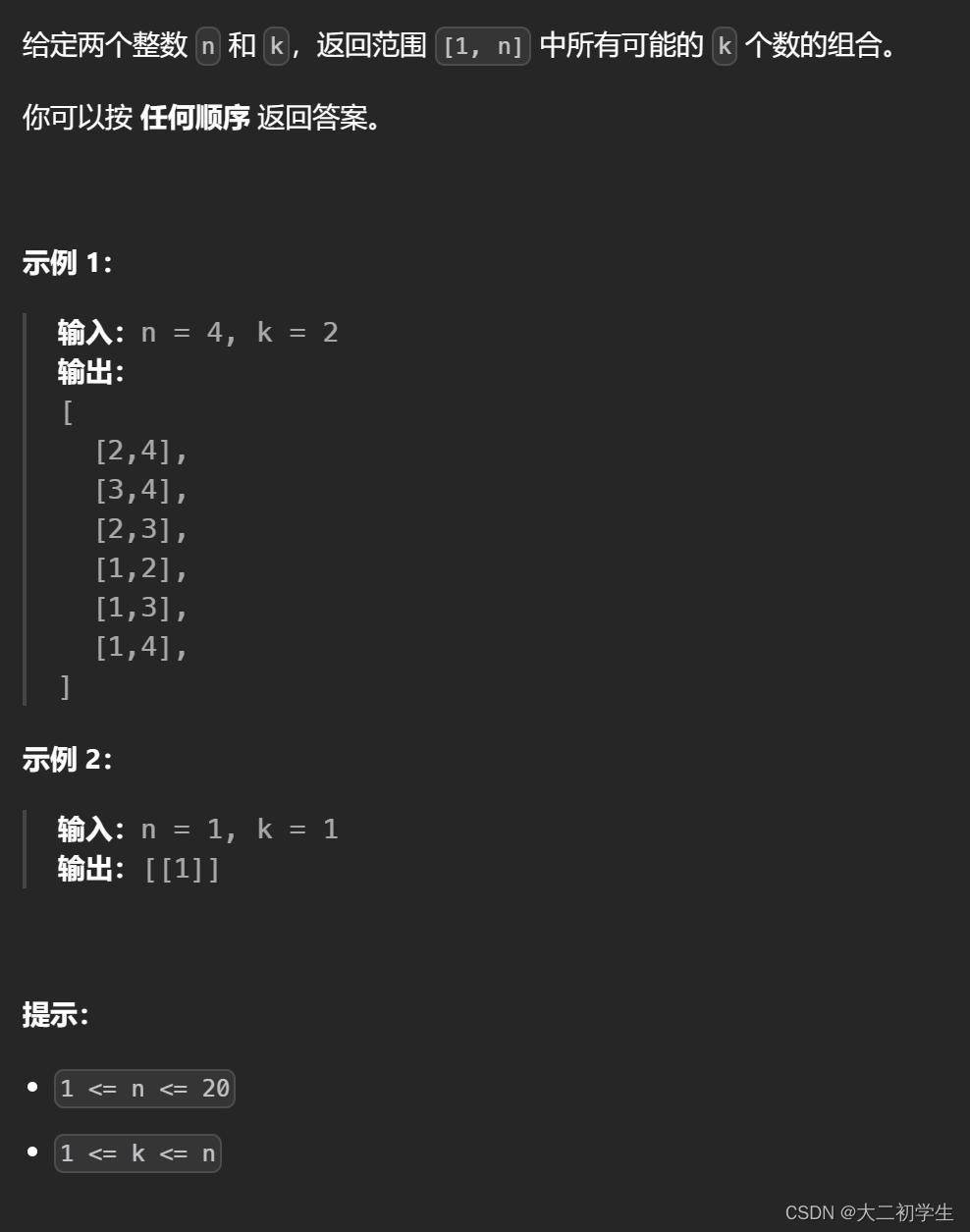
代码:
class Solution {
public:
vector<vector<int>> res;
vector<int> tmp;
void backtracking(int n, int k, int start){
if(tmp.size() == k){
res.push_back(tmp);
return;
}
for(int i = start; i <= n; i++){
tmp.push_back(i);
backtracking(n, k, i + 1);
tmp.pop_back();
}
}
vector<vector<int>> combine(int n, int k) {
backtracking(n, k, 1);
return res;
}
};回溯模板:
void backtracking(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
处理节点;
backtracking(路径,选择列表); // 递归
回溯,撤销处理结果
}
}回溯就是暴力算法,本组合问题实质可以想象成一颗有很多层的树,从根开始往下一层开始选,选了以后再往下一层开始选后面的: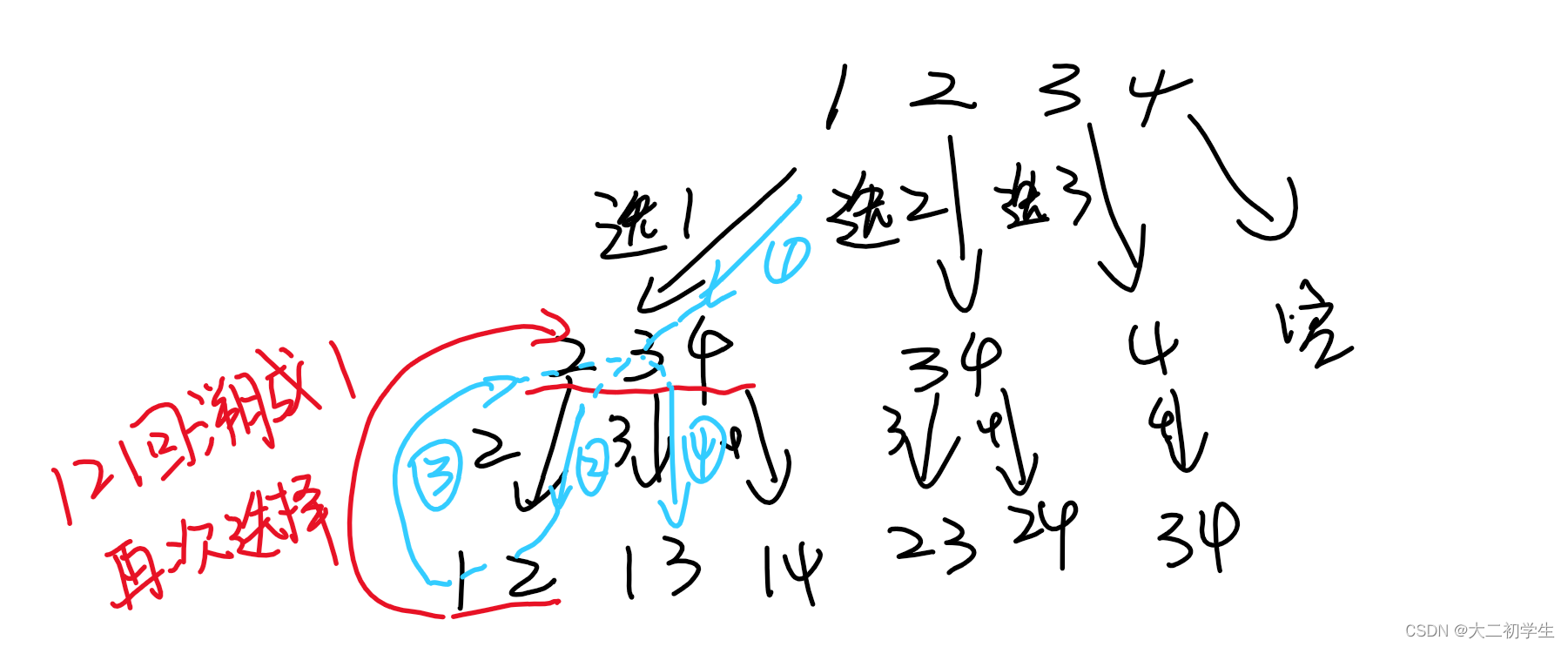
![[Algorithm][回溯][组合][目标和][组合总和]详细讲解](https://img-blog.csdnimg.cn/direct/0eb80903a9d3413aa82d73114f2ce7c8.png)