目录
- 1.组合
- 1.题目链接
- 2.算法原理详解
- 3.代码实现
- 2.目标和
- 1.题目链接
- 2.算法原理详解
- 3.代码实现
- 3.组合总和
- 1.题目链接
- 2.算法原理详解
- 3.代码实现
1.组合
1.题目链接
- 组合
2.算法原理详解
- 思路:每次都只选一个数,此后只能选它后面的数
- 函数设计:
- 全局变量:
vector<vector<int>> retvector<int> path
DFS()设计:void DFS(nums, pos)- 递归出口:
path.size() == k - 剪枝:控制参数,每次从此位置下一个位置开始递归
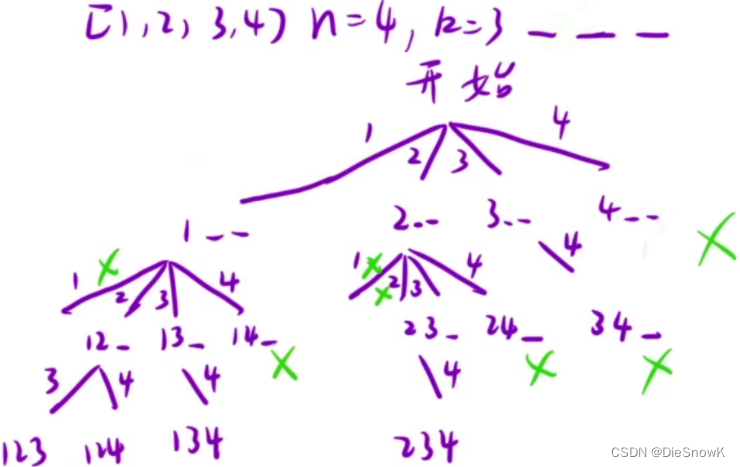
- 全局变量:
3.代码实现
class Solution
{
int _n;
int _k;
vector<vector<int>> ret;
vector<int> path;
public:
vector<vector<int>> combine(int n, int k)
{
_n = n;
_k = k;
DFS(1);
return ret;
}
void DFS(int start)
{
if(path.size() == _k)
{
ret.push_back(path);
}
// 递归 + 剪枝
for(int i = start; i <= _n; i++)
{
path.push_back(i);
DFS(i + 1);
path.pop_back(); // 回溯,恢复现场
}
}
};
2.目标和
1.题目链接
- 目标和
2.算法原理详解
- 本题与子集逻辑几乎相同
- 本题会实现两种代码,可以通过这两种代码来感受:回溯的两种做法
path是全局变量的时候- 本题可能会超时
path作为参数- 此时编译器/代码会代为回溯,每次回溯都省去了一次加/减运算,故效率有所提高
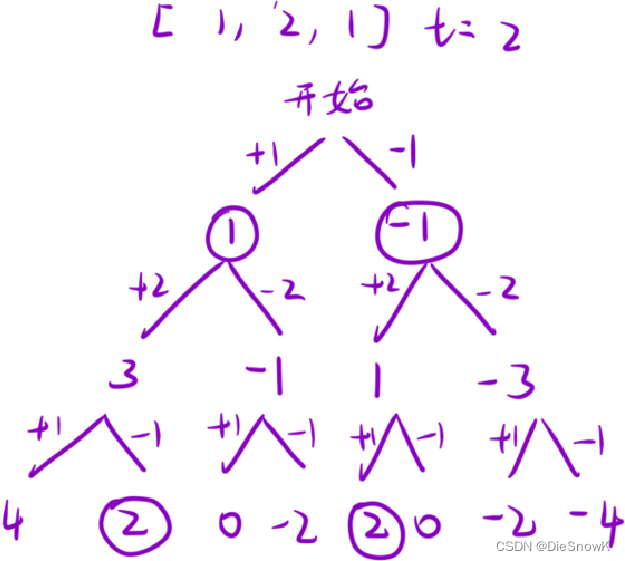
- 此时编译器/代码会代为回溯,每次回溯都省去了一次加/减运算,故效率有所提高
3.代码实现
// v1.0 效率低,可能会超时
class Solution
{
int ret = 0;
int path = 0;
int _target = 0;
public:
int findTargetSumWays(vector<int>& nums, int target)
{
_target = target;
DFS(nums, 0);
return ret;
}
void DFS(vector<int>& nums, int pos)
{
if(pos == nums.size())
{
if(path == _target)
{
ret++;
}
return;
}
// 加
path += nums[pos];
DFS(nums, pos + 1);
path -= nums[pos]; // 回溯,恢复现场
// 减
path -= nums[pos];
DFS(nums, pos + 1);
path += nums[pos]; // 回溯,恢复现场
}
};
--------------------------------------------------------------------------
// v2.0,效率有所改善
class Solution
{
int ret = 0;
int _target = 0;
public:
int findTargetSumWays(vector<int>& nums, int target)
{
_target = target;
DFS(nums, 0, 0);
return ret;
}
void DFS(vector<int>& nums, int pos, int path)
{
if(pos == nums.size())
{
if(path == _target)
{
ret++;
}
return;
}
// 加
DFS(nums, pos + 1, path + nums[pos]);
// 减
DFS(nums, pos + 1, path - nums[pos]);
}
};
3.组合总和
1.题目链接
- 组合总和
2.算法原理详解
-
思路一:每次都只选一个数,此后只能选它及它后面的数
- 函数设计:
- 全局变量:
vector<vector<int>> retvector<int> path
DFS()设计:void DFS(nums, pos, sum)- 递归出口:
sum == _target || (sum > _target || pos == nums.size()) - 回溯:通过
sum控制回溯 - 剪枝:控制
pos参数,每次从此位置开始递归
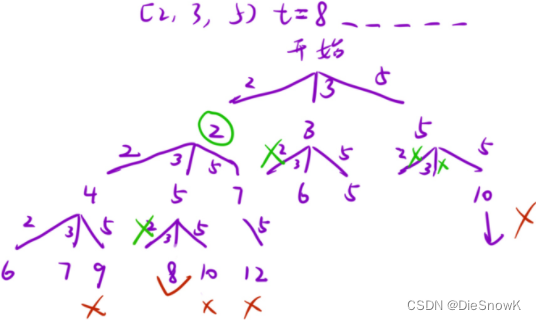
- 全局变量:
- 函数设计:
-
思路二:每次枚举一个数,出现几次
- 函数设计:
- 全局变量:
vector<vector<int>> retvector<int> path
DFS()设计:void DFS(nums, pos, sum)- 递归出口:
sum == _target || (sum > _target || pos == nums.size()) - 回溯:通过
sum控制回溯 - 剪枝:控制
pos参数,每次从此位置开始递归
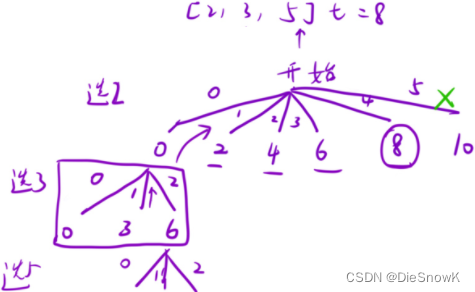
- 全局变量:
- 函数设计:
3.代码实现
// v1.0 每次都只选一个数,此后只能选它及它后面的数
class Solution
{
int _target;
vector<int> path;
vector<vector<int>> ret;
public:
vector<vector<int>> combinationSum(vector<int>& nums, int target)
{
_target = target;
DFS(nums, 0, 0);
return ret;
}
void DFS(vector<int>& nums, int pos, int sum)
{
if(sum == _target)
{
ret.push_back(path);
return;
}
if(sum > _target || pos == nums.size())
{
return;
}
// 递归决策 + 剪枝
for(int i = pos; i < nums.size(); i++)
{
path.push_back(nums[i]);
DFS(nums, i, sum + nums[i]);
path.pop_back(); // 回溯,恢复现场
}
}
};
--------------------------------------------------------------------------
// v2.0 每次枚举一个数,出现几次
class Solution
{
int _target;
vector<int> path;
vector<vector<int>> ret;
public:
vector<vector<int>> combinationSum(vector<int>& nums, int target)
{
_target = target;
DFS(nums, 0, 0);
return ret;
}
void DFS(vector<int>& nums, int pos, int sum)
{
if(sum == _target)
{
ret.push_back(path);
return;
}
if(sum > _target || pos == nums.size())
{
return;
}
// 枚举个数 + 剪枝
for(int i = 0; i * nums[pos] + sum <= _target; i++)
{
if(i)
{
path.push_back(nums[pos]);
}
DFS(nums, pos + 1, i * nums[pos] + sum);
}
// 回溯,恢复现场
for(int i = 1; i * nums[pos] + sum <= _target; i++)
{
path.pop_back();
}
}
};