平衡三进制小数详解与进制转换

标准三进制是“逢三进一，退一还三”的机制，平衡三进制与之类似，但就是偏移了一下变得对称了，平衡三进制与标准三进制可以相互转换，但这样显得有点多余了，所以这里只讲平衡三进制与十进制的转换。

数字系统的由来

远古时代：原始人通过绳子系绳结、在石头或木头上刻划痕的方式来记数，这种计数方法简单，但难数，时间过久了就难以分清那个是那个了。

非位置化数字系统：罗马数字(经典代表)，罗马数字共有7个，分别是Ⅰ（1）、Ⅴ（5）、Ⅹ（10）、Ⅼ（50）、Ⅽ（100）、Ⅾ（500）和Ⅿ（1000），若为ⅤⅤⅤ则表示15。

位置化数字系统：现在用的基本都是这个，如：二进制、平衡三进制、十进制等，计算金钱的用的也是位置化数字系统，它与我们的生活息息相关。

位置化系统的位权

以小数点为分界线，整数的第一位为0，向前一位为1，再向前一位为2，依次类推；然后是小数部分，第一位为-1，向后一位为-2，再后一位为-3依次类推；位置化系统的位权作为系数，若基数为十，则称为十进制、若基数为2，则称为二进制、若基数为3，则称为标准三进制或平衡三进制，如下表所示：

位置化系统的位权	2	1	0		-1	-2	-3
十进制数(125.345)	1	2	5	.	3	4	5
	10^2	10^1	10^0		10^-1	10^-2	10^-3
平衡三进制数(1TT.111)	1	T	T	.	1	1	1
	3^2	3^1	3^0		3^-1	3^-2	3^-3

平衡三进制的小数表示

这是一个绕不开的问题，要想搞明白平衡三进制的小数如何表示，怎么来的那就先搞懂十进制的小数与整数，如上表十进制数为125.345，也就是：

1*10^2 + 2*10^1 + 5*10^0 + 3*10^-1 + 4*10^-2 + 5*10^-3

=100 + 20 + 5 + 0.3 + 0.04 +0.005

=125.345

所以平衡三进制1TT.111(十进制5.5)，可表示为：

1*3^2 + T*3^1 + T*3^0 + 1*3^-1 + 1*3^-2 + 1*3^-3

=9 + (-3) + (-1) + (1/3) + (1/9) + (1/27)

大概为5.4，要精确到后5位，这样的结果较为准确，1TT.11111重新计算结果为5.46095.

平衡三进制转换的运算规则

平衡三进制作为标准三进制的一个变体，所以还是以标准三进制出发，然后再进一步去除得到最终的平衡三进制转换方法。

标准三进制转平衡三进制的方法

平衡三进制的转转换法中，需要先写出一个给定的数 x 在标准三进制中的表示。当 x 是用标准三进制表示时，其数字的每一位都是 0、1 或 2。要转化为平衡三进制，需要从低位到高位操作

遇到 0 和 1，可直接跳过
遇到 2，当前位改为 T，向前进位加上 1
遇到 3，当前位改为 0，向前进位加上 1

十进制整数直接转平衡三进制的方法

   每次进行模3取余，最后进行倒序读取，有以下得余数表示，
   -2   -1   0   1   2（正数与负数分别对2与-2处理）
   -1、0、1合法的，故不处理
   若商为-2，则将商减一，再除于3得到新商，然后余数变成1
   若商为 2，则将商加一，再除于3得到新商，然后余数变成-1

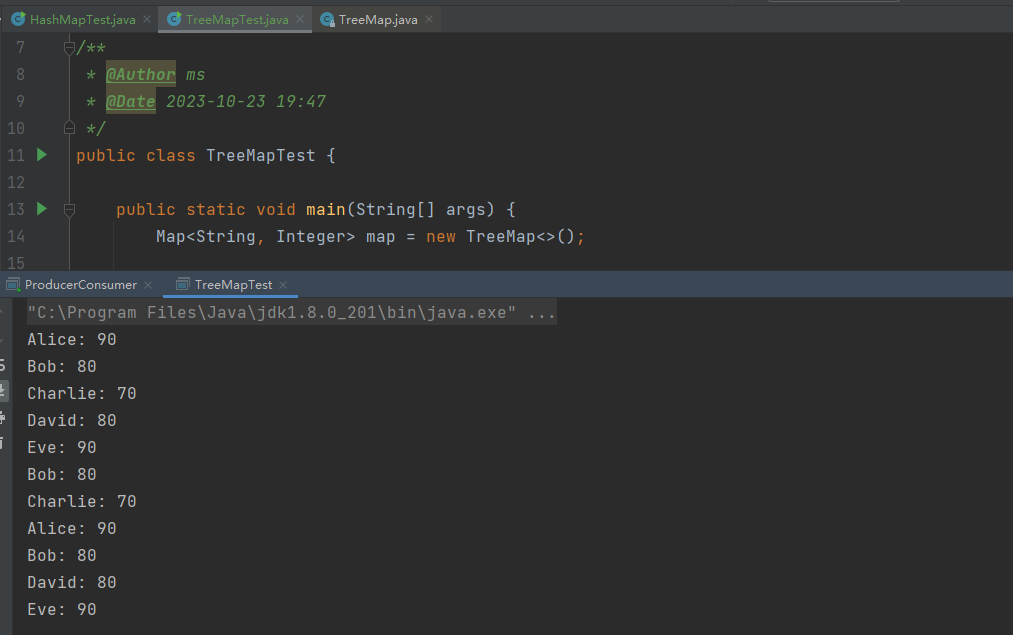
如上图所示，先用连除法，不断的除于3取余，商至到为0结束，标准三进制得到的数为20，然后用第一个规则(标三转平三)，得到1T0；然后直接跳过标准三进制，当商为 2，则将商加一，再除于3得到新商为1，然后余数变成-1，直接得1T0，这样就不用转来转去了。

十进制小数直接转平衡三进制的方法

   每次进行乘3取整，正数结果为正，负数则为负，那么会有以下得整数表示，
   -2   -1   0   1   2（正数与负数分别对2与-2处理）
   若为正数，则遇到0或1直接跳过，遇到2当前位改T，向前进1
   若为负数，则遇到0或1直接跳过，遇到-2当前位改1，向前进T

如上图所示，小数用的是连乘法，不断的乘于3取整，可以精确到某一位或为0为止，标准三进制得到0.3为0.022002，然后用第一个规则(标三转平三)，得到0.10T01T；然后直接跳过标准三进制，遇到0或1直接跳过，遇到2当前位改T，向前进1，也就是向上进1，直接得到0.10T01T，得到正数直接可以(1变T,T变1)变为负数，也可以再算一次。

总结：

整数部分与小数部分要分开算，得到相应结果，最后再相加在一起就行了；

整数部分使用连除法，采用倒序读取余数，即可以得结果；

小数部分使用连乘法，采用正序读取整数，即可以得结果；

十进制浮点数转平衡三进制数的实现

先观察上图，平衡三进制数，它的小数很有特点，就是以0.5或-0.5为分界，它过了这条界则要向前进一位，上面与下面的数也是对称，所以如果是4.5转成平衡三进制，则为11.11111111，当为4.6时，则0.6为1.TT11和4的11相加，则整数部分要进位，得到1TT.TT11TT11TT，其中小数部分没变，整数变了，所以当小数与整数合体时，大于0.5或小于-0.5的小数要进位，会丢失一位，所以要在前面补0就行了。

然后结合上面的方法，十进制数的整数与小数分别转为平衡三进制，再将它们结合在一起就可以了，这里用C++成功实现了上述方法，采用的是deque容器数据结构，它可以高效的在前后两端推入数据，类似于数组但不是数组，因为要进位所以用deque容器，当输入去的数据再拿出来改时方便，平衡三进制的小数和它的分数其实都各有优势，但我更喜欢分数(方便计算，误差小)。

平衡三进制和十进制一样，用小数点分隔整数部分和小数部分；在平衡三进制中，四舍五入和截位的操作是等效的；平衡三进制可以像十进制一样，可以用小数来表示分数；小数可分为：有限小数、无限循环小数、无限不循环小数，小数中除无限不循环小数外都可以用分数来表示；最后给出写了几天，终于写出的十进制浮点数转平衡三进制的C++代码：

#include <iostream>
#include <deque>
#include <algorithm>


using namespace std;
// 将deque容器内数据展示出来
void showDequeArray(const deque<char>& charDeque) {
    for (char element : charDeque) {
        cout << element;
    }
    cout << endl;
}
// 将数字转为char
char toTargetChar(int n) {
    switch (n) {
        case -1: return 'T';
        case 0:  return '0';
        case 1:  return '1';
        default: return '\0';
    }
}

//进位操作
void changeCarryChar(deque<char>& originBalancedTernary,char carryChar){
	//默认要进一位，倒着读取再进位
	bool isCarry=true;
	//当前最后一位为originBalancedTernary.size()-1，
	//前一位为originBalancedTernary.size()-2，
	//最后一位改写，前一位判断是否再进位，同样要改写
	for (int i = originBalancedTernary.size()-2; i >= 0; --i) {	
		//若false则不进位，结束循环
		if(!isCarry) break;
		//这是变换进位操作(正数进1，负数进T)
		switch (originBalancedTernary[i]) {
			case '0':
				isCarry=false;
				originBalancedTernary[i]=carryChar;
				break;
			case '1':
				if(carryChar=='T'){
					isCarry=false;
					originBalancedTernary[i]='0';
				}
				else if(carryChar=='1'){
					isCarry=true;
					originBalancedTernary[i]='T';
				}
				break;
			case 'T':
				if(carryChar=='1'){
					isCarry=false;
					originBalancedTernary[i]='0';
				}
				else if(carryChar=='T'){
					isCarry=true;
					originBalancedTernary[i]='1';
				}
				break;
			default:
				break;
		}
	}
}


//将十进制数转换成平衡三进制数
deque<char> decimalToBalancedTernary(double decimal){
	deque<char> balancedTernary;//创建 Vector存结果
	const int maxIterations = 10;//可调整，小数部分的精确位
	/*
	获取整数部分，进行转换操作，
	每次进行模3取余，因为会出现负数，那么会有以下得余数表示，
	-2	-1	0	1	2（正数与负数分别对2与-2处理）
	-1、0、1合法的，故不处理
	若商为-2，则将商减一，再除于3得到新商，然后余数变成1
	若商为 2，则将商加一，再除于3得到新商，然后余数变成-1
	*/
	int integerPart = static_cast<int>(decimal);
	if(integerPart==0)balancedTernary.push_back('0');//默认为0，则出0
    while (integerPart != 0) {
    	int remainder = integerPart % 3;//得到余数
    	switch (remainder) {
			case -1:
			case  2:
				balancedTernary.push_back('T');
				integerPart = (integerPart + 1) / 3;//商加一，除于3是为了得到商
				break;
			case  1:
			case -2:
				balancedTernary.push_back('1');
				integerPart = (integerPart - 1) / 3;//商减一，除于3是为了得到商
				break;
			default:
				balancedTernary.push_back('0');
				integerPart /= 3;//除于3是为了得到商
				break;
		}
    }
	reverse(balancedTernary.begin(), balancedTernary.end()); // 反转顺序，倒序读取
	
	balancedTernary.push_back('.');//添加小数点
	/*
	获取小数部分，进行转换操作，
	每次进行乘3取整，正数结果为正，负数则为负，那么会有以下得整数表示，
	-2	-1	0	1	2（正数与负数分别对2与-2处理）
	若为正数，则遇到0或1直接跳过，遇到2当前位改T，向前进1
	若为负数，则遇到0或1直接跳过，遇到-2当前位改1，向前进T
	*/
	double fractionalPart = decimal - static_cast<int>(decimal);
	//大于0.5或小于-0.5的小数要进位，当小数与整数合体时，会丢失一位，所以要在前面补0
	if(fractionalPart>0.5 || fractionalPart < -0.5)balancedTernary.push_front('0');
    for (int i = 0; i < maxIterations; ++i) {
		fractionalPart*=3;
		int roundIndex = static_cast<int>(fractionalPart);//乘3后取整的数
		switch (roundIndex) {
			case -2:
				balancedTernary.push_back('1');
				changeCarryChar(balancedTernary,'T');
			break;	
			case 2:
				balancedTernary.push_back('T');
				changeCarryChar(balancedTernary,'1');
			break;
			default:
				balancedTernary.push_back(toTargetChar(roundIndex));
				break;
		}
		fractionalPart-=roundIndex;//得到剩下的小数	
    	if (fractionalPart == 0) break;// 如果小数部分已经处理完毕，退出循环
    }

	return balancedTernary;
}

int main()
{
	double decimal;
	cout<<"请输入十进制浮点数，将转换成平衡三进制:"<<endl;
	cin >> decimal;
	deque<char> balancedTernary = decimalToBalancedTernary(decimal);
	showDequeArray(balancedTernary);
	return 0;
}