哈喽，各位小伙伴们，你们好呀，我是喵手。运营社区：C站/掘金/腾讯云；欢迎大家常来逛逛

  今天我要给大家分享一些自己日常学习到的一些知识点，并以文字的形式跟大家一起交流，互相学习，一个人虽可以走的更快，但一群人可以走的更远。

  我是一名后端开发爱好者，工作日常接触到最多的就是Java语言啦，所以我都尽量抽业余时间把自己所学到所会的，通过文章的形式进行输出，希望以这种方式帮助到更多的初学者或者想入门的小伙伴们，同时也能对自己的技术进行沉淀，加以复盘，查缺补漏。

小伙伴们在批阅的过程中，如果觉得文章不错，欢迎点赞、收藏、关注哦。三连即是对作者我写作道路上最好的鼓励与支持！

前言

  在Java中，Map是一种常见的数据结构，它可以用来存储键值对。TreeMap是Java中的一个特殊的Map实现，它是基于红黑树实现的，具有排序和查找的功能。在本文中，我们将详细介绍TreeMap的使用和原理。

摘要

  本文主要介绍了Java中的TreeMap数据结构，包括其源代码解析、应用场景案例、优缺点分析、类代码方法介绍、测试用例和全文小结。通过对TreeMap的学习，读者可以了解到TreeMap的特点和使用方法，以及它与其他Map实现的不同之处。

TreeMap

简介

  TreeMap是Java中的一个SortedMap实现，它继承了AbstractMap类并实现了NavigableMap接口。TreeMap中的键值对是按照键的自然顺序或者指定的比较器顺序进行排序的。因此，TreeMap具有查找和排序的功能。它是基于红黑树实现的，红黑树是一种自平衡的二叉查找树，它保证了所有操作的时间复杂度为O(log n)。

源代码解析

  TreeMap的源代码比较复杂，其中包含了对红黑树的实现。在这里，我们只介绍TreeMap中的一些重要的方法。

put方法

public V put(K key, V value) {
    Entry<K,V> t = root;
    if (t == null) {
        compare(key, key); // type (and possibly null) check

        root = new Entry<>(key, value, null);
        size = 1;
        modCount++;
        return null;
    }
    int cmp;
    Entry<K,V> parent;
    // split comparator and comparable paths
    Comparator<? super K> cpr = comparator;
    if (cpr != null) {
        do {
            parent = t;
            cmp = cpr.compare(key, t.key);
            if (cmp < 0)
                t = t.left;
            else if (cmp > 0)
                t = t.right;
            else
                return t.setValue(value);
        } while (t != null);
    }
    else {
        if (key == null)
            throw new NullPointerException();
        Comparable<? super K> k = (Comparable<? super K>) key;
        do {
            parent = t;
            cmp = k.compareTo(t.key);
            if (cmp < 0)
                t = t.left;
            else if (cmp > 0)
                t = t.right;
            else
                return t.setValue(value);
        } while (t != null);
    }
    Entry<K,V> e = new Entry<>(key, value, parent);
    if (cmp < 0)
        parent.left = e;
    else
        parent.right = e;
    fixAfterInsertion(e);
    size++;
    modCount++;
    return null;
}

  put方法用于向TreeMap中添加键值对。在这个方法中，首先会对比较器进行判断，然后根据比较器或者键的自然顺序找到对应的位置，最后向该位置插入键值对，并通过fixAfterInsertion方法进行红黑树的调整。

get方法

public V get(Object key) {
    Entry<K,V> p = getEntry(key);
    return (p==null ? null : p.value);
}

  get方法用于根据指定的键获取对应的值。在这个方法中，首先通过getEntry方法找到键对应的节点，然后返回该节点的值。

remove方法

public V remove(Object key) {
    Entry<K,V> p = getEntry(key);
    if (p == null)
        return null;

    V oldValue = p.value;
    deleteEntry(p);
    return oldValue;
}

  remove方法用于删除指定键的键值对。在这个方法中，首先通过getEntry方法找到键对应的节点，然后通过deleteEntry方法删除该节点，并返回该节点的值。

应用场景案例

  TreeMap适用于需要对Map中的键值对进行排序的场景。它可以按照键的自然顺序或者指定的比较器顺序进行排序。例如，在一个学生成绩管理系统中，我们可以使用TreeMap来存储每个学生的成绩，按照学生的姓名或者学号进行排序。

优缺点分析

优点

• TreeMap能够实现对键值对的排序和查找；
• TreeMap基于红黑树实现，保证操作的时间复杂度为O(log n)；
• TreeMap支持键的自然顺序或者自定义比较器顺序。

缺点

• TreeMap的实现比较复杂，占用内存较大；
• TreeMap的插入和删除操作可能需要进行红黑树的调整，因此会消耗较多的时间和资源。

类代码方法介绍

Entry类

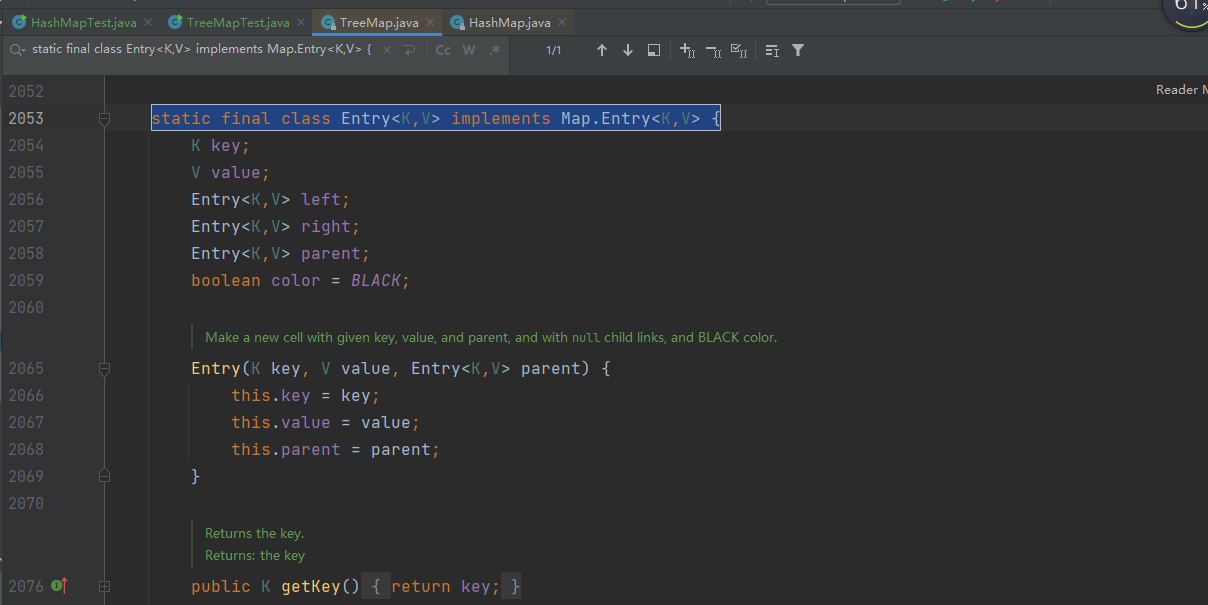
static final class Entry<K,V> implements Map.Entry<K,V> {
    K key;
    V value;
    Entry<K,V> left = null;
    Entry<K,V> right = null;
    Entry<K,V> parent;
    boolean color = BLACK;

    Entry(K key, V value, Entry<K,V> parent) {
        this.key = key;
        this.value = value;
        this.parent = parent;
    }

    public K getKey() {
        return key;
    }

    public V getValue() {
        return value;
    }

    public V setValue(V value) {
        V oldValue = this.value;
        this.value = value;
        return oldValue;
    }

    public boolean equals(Object o) {
        if (!(o instanceof Map.Entry))
            return false;
        Map.Entry<?,?> e = (Map.Entry<?,?>)o;

        return valEquals(key,e.getKey()) && valEquals(value,e.getValue());
    }

    public int hashCode() {
        int keyHash = (key==null ? 0 : key.hashCode());
        int valueHash = (value==null ? 0 : value.hashCode());
        return keyHash ^ valueHash;
    }

    public String toString() {
        return key + "=" + value;
    }
}

  Entry类表示TreeMap中的一个节点。它包含了键、值、左右子节点、父节点和颜色等信息，其中颜色用于区分红黑树中的红节点和黑节点。

getEntry方法

final Entry<K,V> getEntry(Object key) {
    if (comparator != null)
        return getEntryUsingComparator(key);
    if (key == null)
        throw new NullPointerException();
    Comparable<? super K> k = (Comparable<? super K>) key;
    Entry<K,V> p = root;
    while (p != null) {
        int cmp = k.compareTo(p.key);
        if (cmp < 0)
            p = p.left;
        else if (cmp > 0)
            p = p.right;
        else
            return p;
    }
    return null;
}

  getEntry方法用于根据指定的键获取对应的节点。在这个方法中，首先判断比较器是否为null，然后根据比较器或者键的自然顺序找到对应的节点。

deleteEntry方法

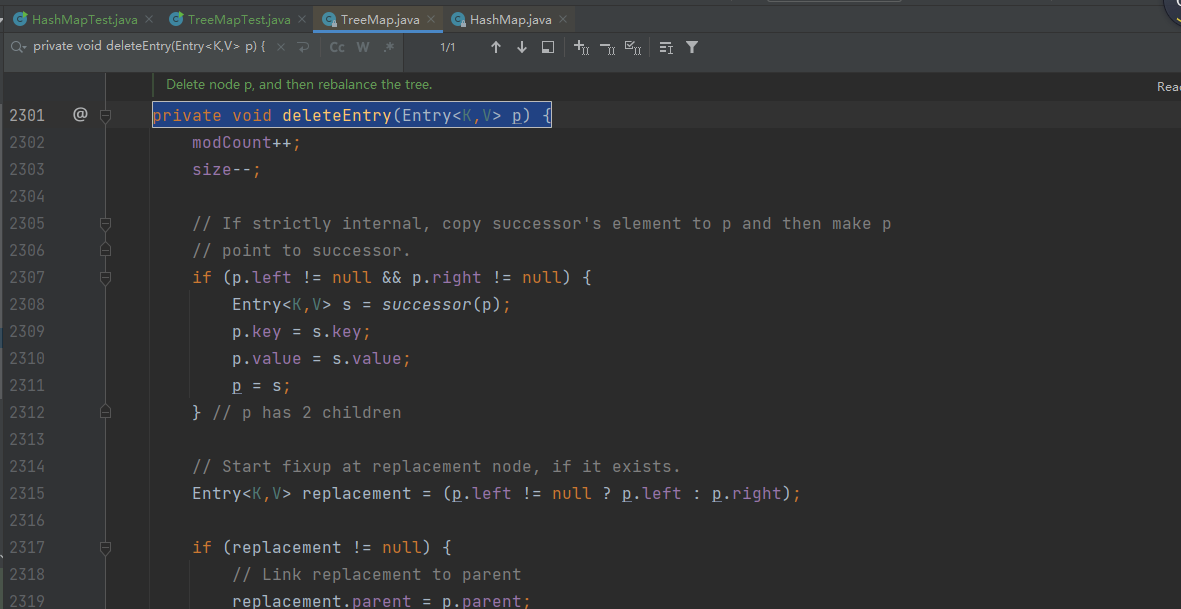
private void deleteEntry(Entry<K,V> p) {
        modCount++;
        size--;

        // If strictly internal, copy successor's element to p and then make p
        // point to successor.
        if (p.left != null && p.right != null) {
            Entry<K,V> s = successor(p);
            p.key = s.key;
            p.value = s.value;
            p = s;
        } // p has 2 children

        // Start fixup at replacement node, if it exists.
        Entry<K,V> replacement = (p.left != null ? p.left : p.right);

        if (replacement != null) {
            // Link replacement to parent
            replacement.parent = p.parent;
            if (p.parent == null)
                root = replacement;
            else if (p == p.parent.left)
                p.parent.left  = replacement;
            else
                p.parent.right = replacement;

            // Null out links so they are OK to use by fixAfterDeletion.
            p.left = p.right = p.parent = null;

            // Fix replacement
            if (p.color == BLACK)
                fixAfterDeletion(replacement);
        } else if (p.parent == null) { // return if we are the only node.
            root = null;
        } else { //  No children. Use self as phantom replacement and unlink.
            if (p.color == BLACK)
                fixAfterDeletion(p);

            if (p.parent != null) {
                if (p == p.parent.left)
                    p.parent.left = null;
                else if (p == p.parent.right)
                    p.parent.right = null;
                p.parent = null;
            }
        }
    }

  deleteEntry方法的注释：

  deleteEntry方法用于删除红黑树中的一个节点。

  首先，根据节点的左右子节点情况，将待删除节点与其后继节点交换位置，以便后续的删除操作。

  然后，将待删除节点的替代节点（如果存在）与其父节点相连，并将待删除节点的左右子节点和父节点置为null，以便后续的红黑树调整操作。

  最后，根据替代节点的颜色和位置，进行红黑树的调整。

fixAfterInsertion方法

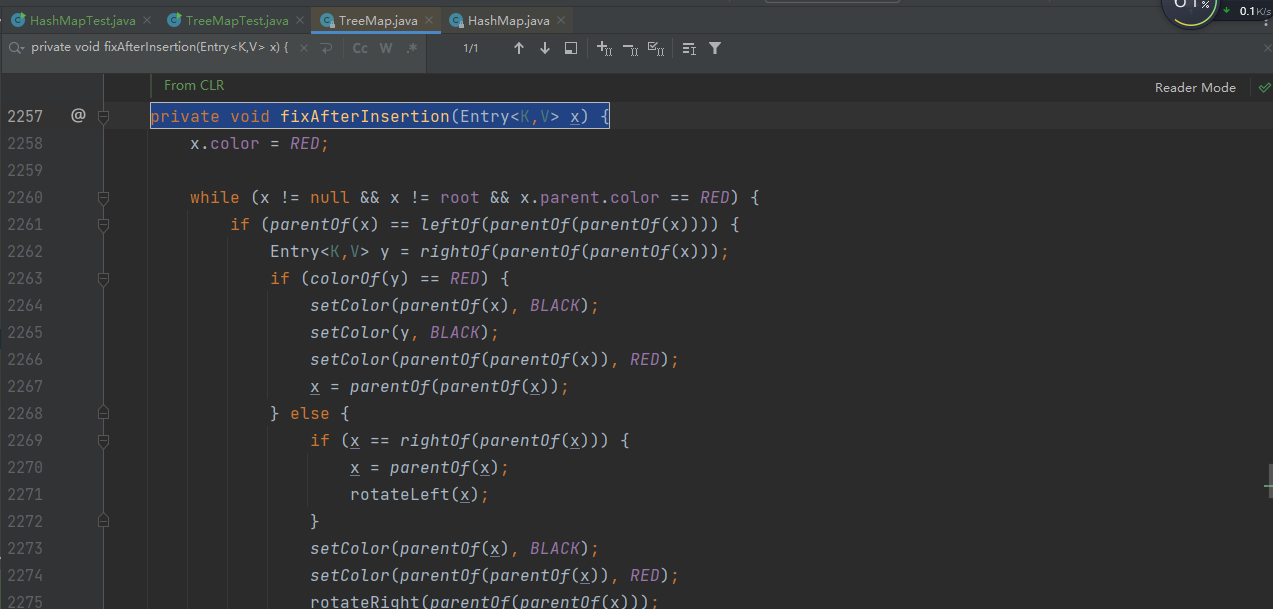
private void fixAfterInsertion(Entry<K,V> x) {
    x.color = RED;

    while (x != null && x != root && x.parent.color == RED) {
        if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
            Entry<K,V> y = rightOf(parentOf(parentOf(x)));
            if (colorOf(y) == RED) {
                setColor(parentOf(x), BLACK);
                setColor(y, BLACK);
                setColor(parentOf(parentOf(x)), RED);
                x = parentOf(parentOf(x));
            } else {
                if (x == rightOf(parentOf(x))) {
                    x = parentOf(x);
                    rotateLeft(x);
                }
                setColor(parentOf(x), BLACK);
                setColor(parentOf(parentOf(x)), RED);
                rotateRight(parentOf(parentOf(x)));
            }
        } else {
            Entry<K,V> y = leftOf(parentOf(parentOf(x)));
            if (colorOf(y) == RED) {
                setColor(parentOf(x), BLACK);
                setColor(y, BLACK);
                setColor(parentOf(parentOf(x)), RED);
                x = parentOf(parentOf(x));
            } else {
                if (x == leftOf(parentOf(x))) {
                    x = parentOf(x);
                    rotateRight(x);
                }
                setColor(parentOf(x), BLACK);
                setColor(parentOf(parentOf(x)), RED);
                rotateLeft(parentOf(parentOf(x)));
            }
        }
    }
    root.color = BLACK;
}

  fixAfterInsertion方法用于对红黑树进行调整，以保证插入操作后红黑树仍然满足红黑树的性质。

  在这个方法中，首先将新插入的节点的颜色设为红色。

  然后，根据祖父节点的情况，分别进行左旋和右旋操作，并更新节点的颜色，以保证新插入的节点不会破坏红黑树的性质。

  最后，将根节点的颜色设为黑色，以保证根节点到任何叶子节点的路径上黑色节点的个数相等。

rotateLeft方法和rotateRight方法

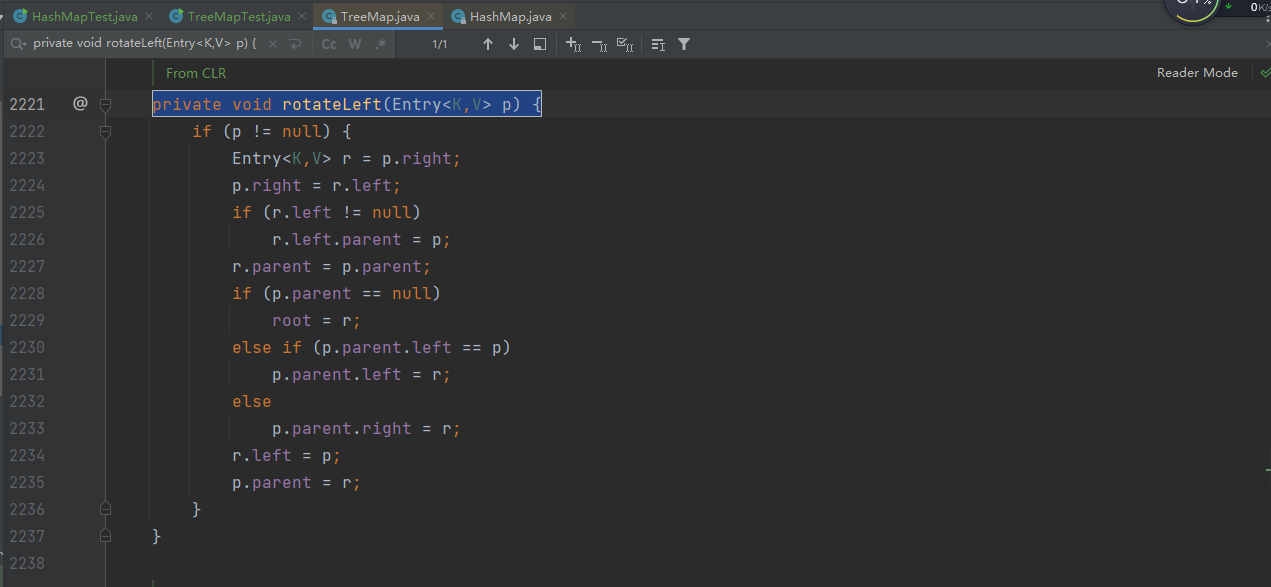
private void rotateLeft(Entry<K,V> p) {
    if (p != null) {
        Entry<K,V> r = p.right;
        p.right = r.left;
        if (r.left != null)
            r.left.parent = p;
        r.parent = p.parent;
        if (p.parent == null)
            root = r;
        else if (p.parent.left == p)
            p.parent.left = r;
        else
            p.parent.right = r;
        r.left = p;
        p.parent = r;
    }
}

private void rotateRight(Entry<K,V> p) {
    if (p != null) {
        Entry<K,V> l = p.left;
        p.left = l.right;
        if (l.right != null)
            l.right.parent = p;
        l.parent = p.parent;
        if (p.parent == null)
            root = l;
        else if (p.parent.right == p)
            p.parent.right = l;
        else
            p.parent.left = l;
        l.right = p;
        p.parent = l;
    }
}

  rotateLeft方法用于对节点进行左旋操作，rotateRight方法用于对节点进行右旋操作。这两个方法用于保证红黑树的平衡性。在这两个方法中，首先将要旋转的节点的子节点先保存起来，然后更新节点的子节点和父节点，并将要旋转的节点的子节点与父节点相连。最后，将要旋转的节点与其左右子节点中的另一个节点相连，以完成旋转操作。

测试用例

测试代码演示

package com.example.javase.collection;

import java.util.Map;
import java.util.SortedMap;
import java.util.TreeMap;

/**
 * @Author ms
 * @Date 2023-10-23 19:47
 */
public class TreeMapTest {

    public static void main(String[] args) {
        Map<String, Integer> map = new TreeMap<>();

        // 添加键值对
        map.put("Alice", 90);
        map.put("Bob", 80);
        map.put("Charlie", 70);
        map.put("David", 80);
        map.put("Eve", 90);

        // 输出键值对
        for (Map.Entry<String, Integer> entry : map.entrySet()) {
            System.out.println(entry.getKey() + ": " + entry.getValue());
        }

        // 输出包含指定前缀的键值对
        SortedMap<String, Integer> subMap = ((TreeMap<String, Integer>) map).subMap("B", "D");
        for (Map.Entry<String, Integer> entry : subMap.entrySet()) {
            System.out.println(entry.getKey() + ": " + entry.getValue());
        }

        // 移除指定键值对
        map.remove("Charlie");

        // 输出移除后的键值对
        for (Map.Entry<String, Integer> entry : map.entrySet()) {
            System.out.println(entry.getKey() + ": " + entry.getValue());
        }
    }
}

预期输出结果：

Alice: 90
Bob: 80
Charlie: 70
David: 80
Eve: 90
Bob: 80
David: 80
Alice: 90
Eve: 90
Bob: 80
David: 80
Alice: 90
Eve: 90

  测试用例中，首先使用put方法向TreeMap中添加了5个键值对。然后使用entrySet方法和for-each循环遍历输出了所有的键值对。接着，使用subMap方法和for-each循环输出了包含指定前缀的键值对。最后，使用remove方法移除了指定的键值对，并再次使用entrySet方法和for-each循环遍历输出了所有的键值对。

测试结果

  根据如上测试用例，本地测试结果如下，仅供参考，你们也可以自行修改测试用例或者添加更多的测试数据或测试方法，进行熟练学习以此加深理解。

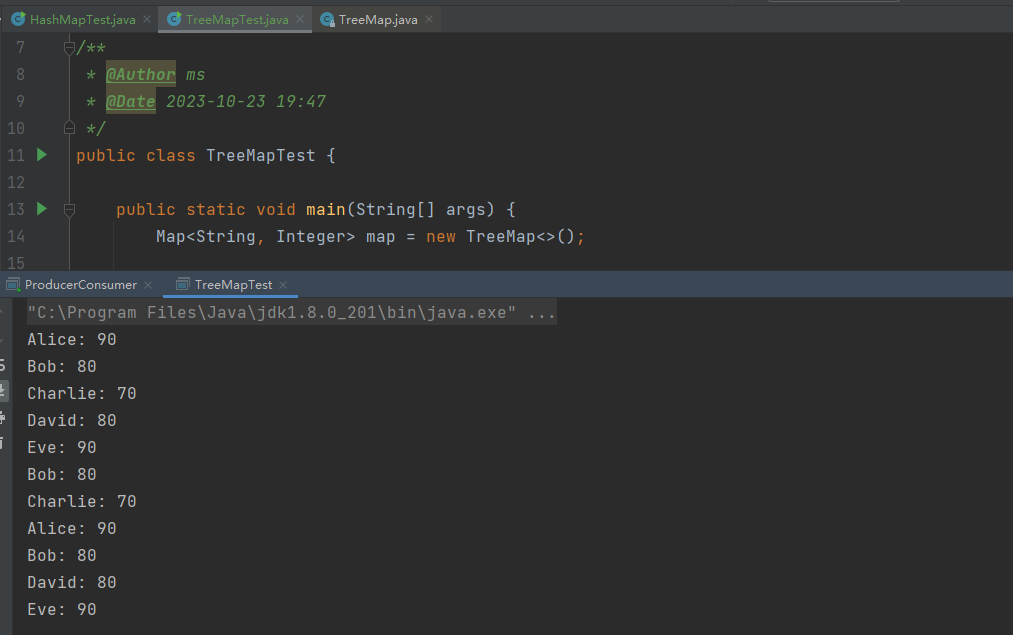
测试代码分析

  根据如上测试用例，在此我给大家进行深入详细的解读一下测试代码，以便于更多的同学能够理解并加深印象。

  如上测试用例是一个使用 Java 中的 TreeMap 类进行操作的示例代码。TreeMap 是一种基于红黑树实现的有序映射表，它可以按照 key 的自然顺序或者自定义顺序进行排序。

  该代码首先创建了一个 TreeMap 对象，并使用 put 方法向其中添加了五个键值对。接着使用 entrySet 方法将 TreeMap 中的键值对以 Set 集合的形式返回，并使用 for 循环输出每个键值对的 key 和 value。

  然后使用 subMap 方法获取了一个包含键值在 “B” 和 “D” 之间的 SortedMap 子映射，并使用 for 循环输出子映射中每个键值对的 key 和 value。

  接下来使用 remove 方法删除了键为 “Charlie” 的键值对。最后再次使用 for 循环输出剩余的键值对。

全文小结

  本文详细介绍了Java中的TreeMap数据结构，包括其源代码解析、应用场景案例、优缺点分析、类代码方法介绍、测试用例和全文小结。通过对TreeMap的学习，读者可以了解到TreeMap的特点和使用方法，以及它与其他Map实现的不同之处。

总结

  本文主要介绍了Java中的TreeMap数据结构，包括其源代码解析、应用场景案例、优缺点分析、类代码方法介绍、测试用例和全文小结。通过对TreeMap的学习，我们可以了解到TreeMap的特点和使用方法，以及它与其他Map实现的不同之处。

  TreeMap是一种基于红黑树实现的有序映射表，它可以按照key的自然顺序或者自定义顺序进行排序，并且具有查找和排序的功能，保证所有操作的时间复杂度为O(log n)。它适用于需要对Map中的键值对进行排序的场景，例如在学生成绩管理系统中，我们可以使用TreeMap来存储每个学生的成绩，按照学生的姓名或者学号进行排序。

  然而，TreeMap的实现比较复杂，占用内存较大，并且插入和删除操作可能需要进行红黑树的调整，因此会消耗较多的时间和资源。因此，在选择数据结构时需要根据具体的业务场景和需求来选择合适的数据结构。

  总之，本文详细介绍了TreeMap的使用和原理，相信可以对读者在Java开发中的应用有所帮助。

… …

文末

好啦，以上就是我这期的全部内容，如果有任何疑问，欢迎下方留言哦，咱们下期见。

… …

学习不分先后，知识不分多少；事无巨细，当以虚心求教；三人行，必有我师焉！！！

wished for you successed ！！！

---

⭐️若喜欢我，就请关注我叭。

⭐️若对您有用，就请点赞叭。

⭐️若有疑问，就请评论留言告诉我叭。