文章目录
- 分支概念
- 分支使用
- 查看分支
- 分支创建
- 分支切换
- 分支合并
- 合并冲突
- 分支删除
- 分支管理
- 快进模式
- 分支策略
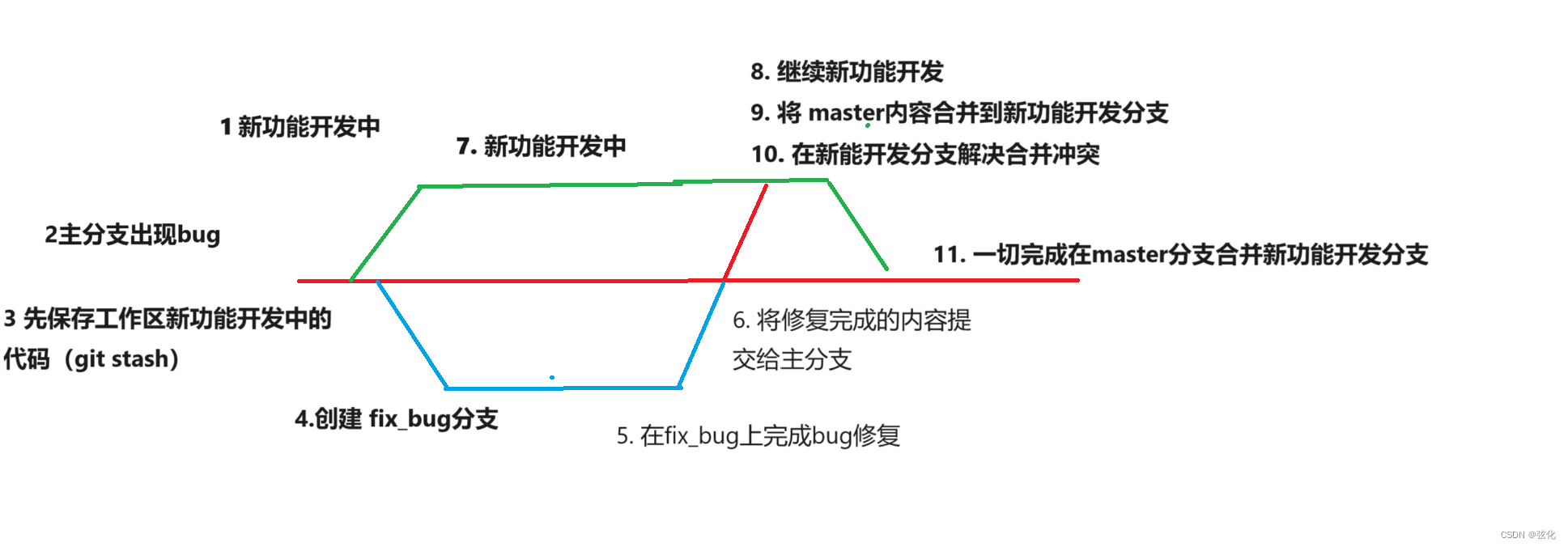
- 内容保存
- 错误处理
分支概念
(1)分支概念
Git分支是指在版本控制系统Git中,用来表示项目的不同工作流程或开发路径的一个重要概念。通过创建分支,可以在不影响主线代码的情况下进行独立的工作或实验。在Git中,每个项目都有一个默认的主分支,通常称为master或main分支。除了主分支外,用户可以根据需要创建任意数量的其他分支。这些分支可以基于主分支创建,也可以基于其他分支创建。分支的主要作用是允许团队成员在不互相干扰的情况下并行开发不同的功能或修复bug。每个分支都是独立的代码空间,允许开发人员自由地提交、合并和回滚更改,而不会影响其他分支或主线代码。
(二) HEAD 含义:
Git 基础使用(1)中提到,HEAD是.git文件夹中的一个重要文件。
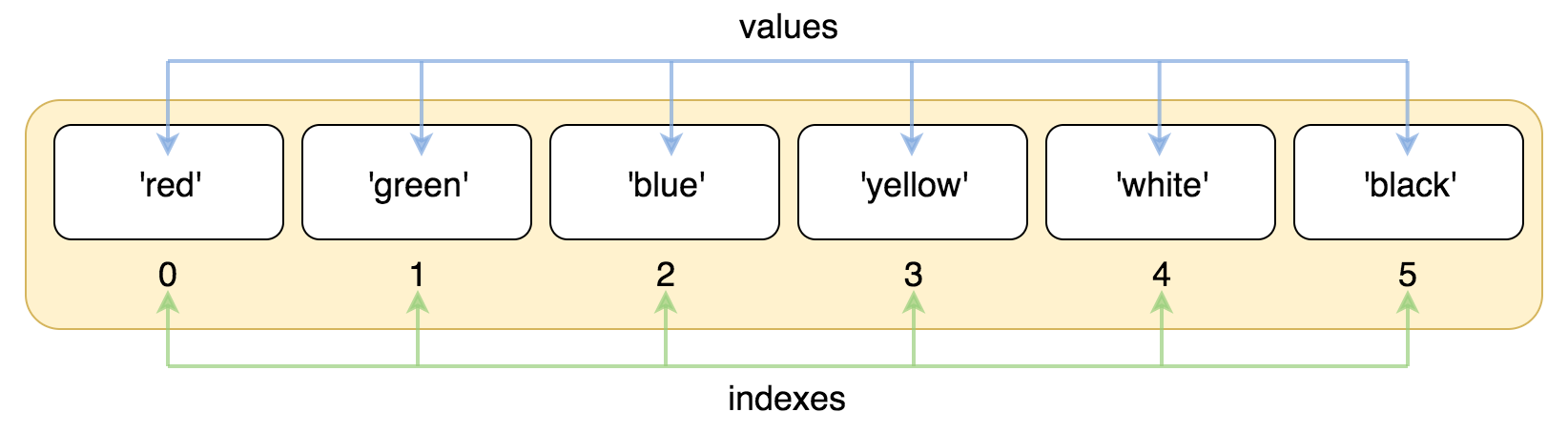
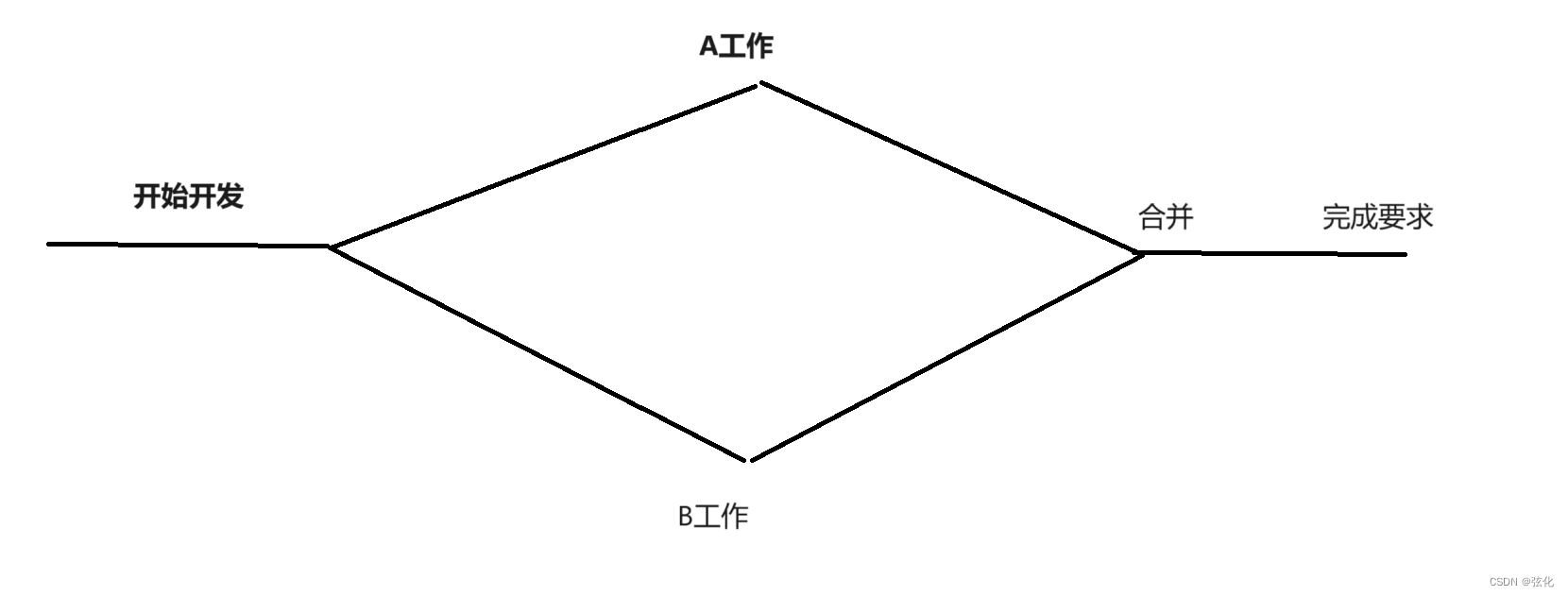
Git 中的 HEAD 是一个指针,指向当前所在的本地分支上最近一次提交的版本。它可以理解为当前工作目录的快照,是我们在代码库中进行操作时的参照点。HEAD:默认指向 master 分⽀。
HEAD作用:
①标识当前位置:HEAD 指示了当前所在的分支以及在该分支上的最新提交。
②切换分支:当我们切换分支时,HEAD 会随之移动到所切换到的分支上,指向该分支上的最新提交
分支使用
查看分支
# 查看所有本地分支,
# 并在当前分支旁边标记一个星号(*)表示当前所在的分支
# 即HEAD指向的分支
git branch

分支创建
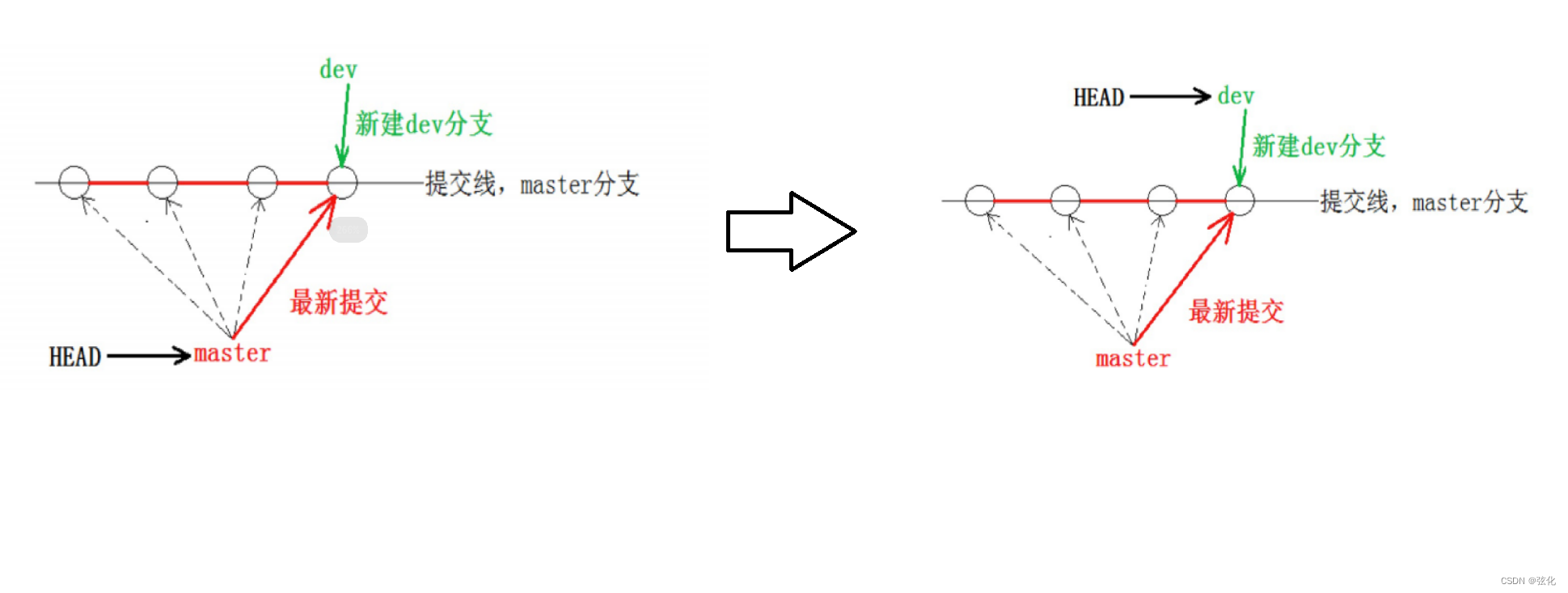
git branch new_branch_name
分支切换
git checkout target_branch_name
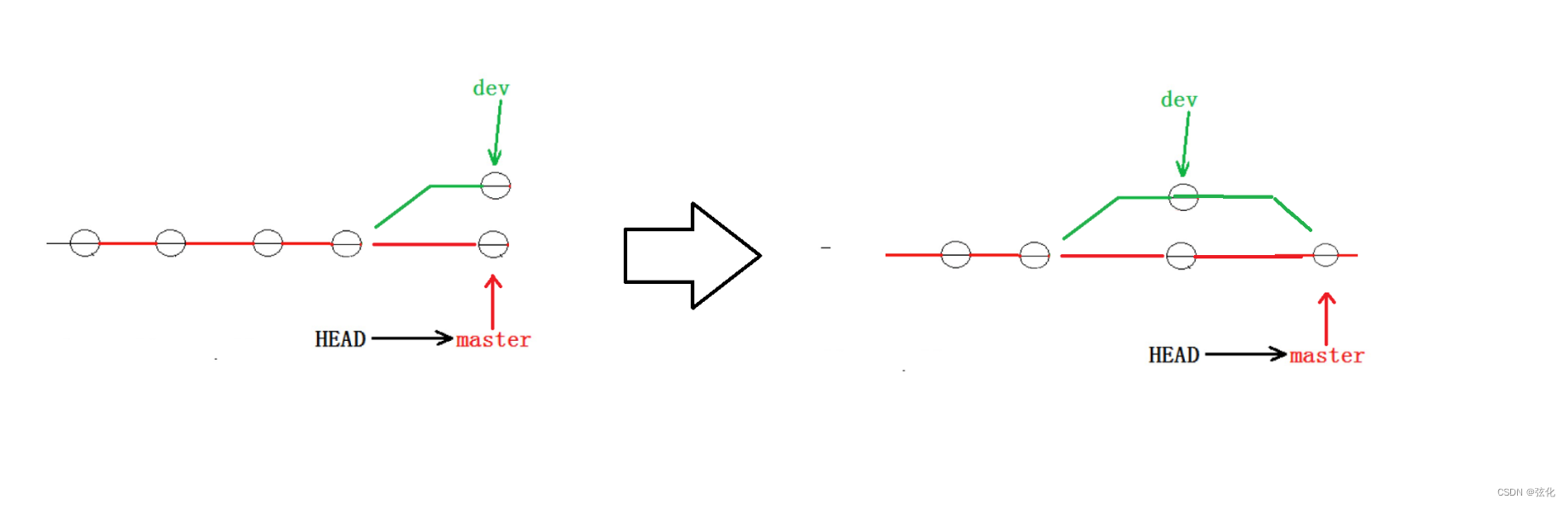
分支合并
因为创建、合并和删除分⽀⾮常快,所以Git⿎励你使⽤分⽀完成某个任务,合并后再删掉分⽀,这和直接在master分⽀上⼯作效果是⼀样的,但过程更安全。
# 首先需要切换到 master 分支
git checkout <target-branch>
# 把 source-branch 分支的更改合并到当前所在的 target-branch 分支上
git merge <source-branch>
合并冲突
<<<<<<< HEAD
// 本地分支的修改内容
=======
// 要合并的分支的修改内容
>>>>>> branch-name
// 在通过文本编辑的方式手动解决冲突之后,需要再次commit
在实际分⽀合并的时候,并不是想合并就能合并成功的,有时候可能会遇到代码冲突的问题。
举例:

分支删除
分支与主分支合并完成后, 该分⽀对于我们来说就没⽤了, 那么dev分⽀就可以被删除掉。注意,如果当前正处于某分⽀下,就不能删除当前分⽀。
// 删除指定分支
// 这个指令会删除指定的分支,前提是该分支已完全合并到当前分支中
git branch -d <branch_name>
//这会强制删除指定分支,即使它包含未合并的更改。
git branch -D <branch_name>
分支管理
快进模式
快进模式(Fast-forward mode)是Git中一种合并分支的方式。当您尝试将一个分支合并到当前分支时,如果当前分支的指针可以直接移动到要合并的分支的最新提交,而不需要创建新的合并提交,Git就会执行快进合并。(发升合并冲突后,手动修改并再次commite就不是Fast-forward mode模式)
在快进模式下,Git会简单地将当前分支指针直接指向要合并的分支的最新提交,从而使得提交历史保持线性。这种合并方式通常发生在没有分支间的提交冲突时,可以帮助保持项目的提交历史整洁和易于理解。
但在在这种 Fast forward 模式下,删除分⽀后,查看分⽀历史时,会丢掉分⽀信息,看不出来最新提交到底是 merge 进来的还是正常提交的。 Git ⽀持我们强制禁⽤ Fast forward 模式,那么就会在 merge 时⽣成⼀个新的 commit ,这样,从分⽀历史上就可以看出分⽀信息。
# 合并分支时禁用快进模式
# 即使是简单的合并操作也会生成一个合并提交,以保留合并的信息。
git merge --no-ff <branch-name>
# 提交
git commite -m
# 查看提交日志
git log
分支策略
常见分支策略如下:
主分支(Master/Main):主分支通常用于存储稳定的、可部署的代码。开发团队应该保持主分支的代码始终是可用和可部署的状态。
开发分支(Develop):开发分支是用于整合各个功能特性的地方。团队成员在各自的特性分支上完成开发后,将其合并到开发分支进行集成测试。
特性分支(Feature Branches):每个新功能或任务应该在单独的特性分支上进行开发。一旦特性完成并通过测试,可以将其合并回开发分支。
发布分支(Release Branches):发布分支用于准备发布新版本。在发布分支上进行最终测试、Bug修复和版本号更新等操作。
修复分支(Hotfix Branches):用于紧急修复生产环境中的Bug的分支。修复完成后,应该将其合并回主分支和开发分支。
内容保存
# git stash 会先存储当前工作区发生的更改,再将将当前工作区发生的更改清除
# 在Git的"堆栈"中,存储当前工作区的内容
git stash
# 用于显示存储的变更列表,运行这个命令后,
# Git会列出所有已经存储的变更以及它们的引用ID
git stash list
# git stash list 结果
# ID(stash@{n})
stash@{0}: WIP on <branch_name>: <commit_message>
stash@{1}: On <branch_name>: <commit_message>
# 它会将最近一次存储的变更应用到当前工作目录中,但并不会从堆栈中移除这个存储项。
git stash apply
# 它会将最近一次存储的变更应用到当前工作目录中,并从堆栈中移除这个存储项。
git stash pop
# 如果你想应用存储的变更并且删除所有存储项
git stash apply stash@{n}
错误处理
(当master分支出现bug,但还有新功能要开发)