目录

1.程序功能描述

2.测试软件版本以及运行结果展示

3.核心程序

4.本算法原理

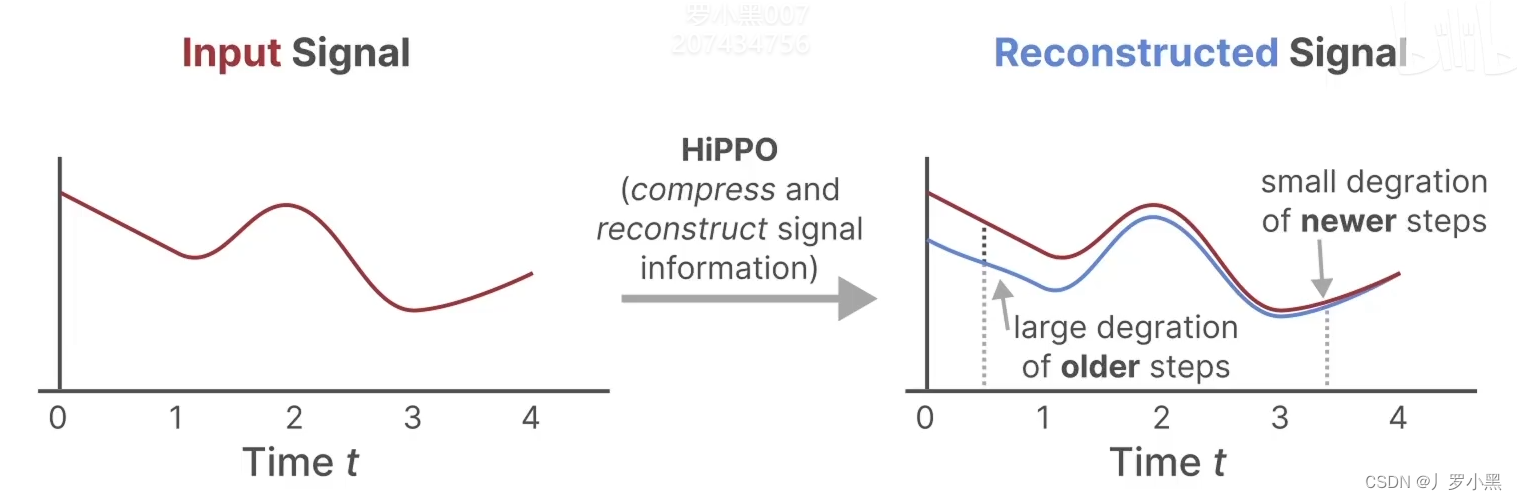
4.1 扩散映射（Diffusion Maps）

4.2 卡尔曼滤波

4.3 基于梯度流的扩散映射卡尔曼滤波（GFDMKF）

5.完整程序

---

1.程序功能描述

        基于梯度流的扩散映射卡尔曼滤波算法的信号预处理matlab仿真。设置不同的噪声大小，测试滤波效果。

2.测试软件版本以及运行结果展示

MATLAB2022A版本运行

3.核心程序

..........................................................................
% 加载数据
load data.mat

SNR     = 10;     % 信噪比
Dims    = 2;      % 扩散映射坐标使用的维度
Ts      = 0.01;   % 时间步长
% 生成测量值：
x0      = atan(ang1./ang2).';       % 清洁角度值
y0      = sqrt(ang1.^2 + ang2.^2).'; % 清洁半径值

x1      = awgn(x0,SNR,'measured'); % 含噪声角度
y1      = awgn(y0,SNR,'measured');  % 含噪声半径
 
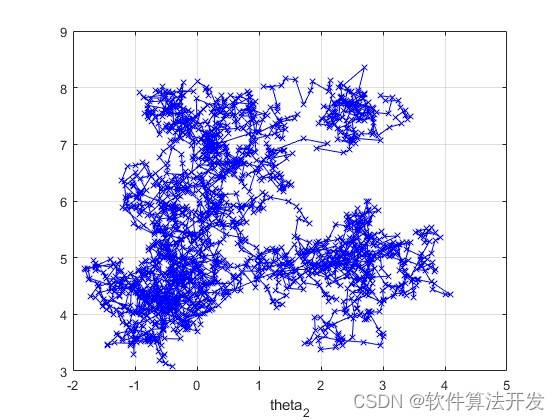
% 绘制状态轨迹：
figure
plot(ang1(1:2000),ang2(1:2000),'b-x')
grid on; 
xlabel('theta_1')
xlabel('theta_2') 

% 使用修改后的马氏距离构建扩散映射
% 计算含噪测量的修改后马氏距离：
distance      = func_dist([x1; y1]);

% 计算扩散映射坐标和特征值：
[xd, lmd]     = func_diffusion(distance, Dims);
% 应用DMK滤波器：
[~, y_est] = func_mk(xd, lmd, [x1; y1], Ts);

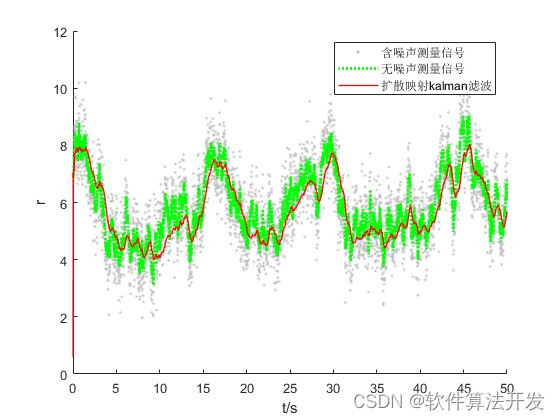
% 绘制不同SNR的轨迹示例：
tt = 1:size([x1; y1],2); 


figure
scatter(tt*Ts,y1,20,[0.75,0.75,0.75],'.'); % 绘制噪声半径测量点
hold on
plot(tt*Ts,y0,'g:','LineWidth',2); % 绘制清洁半径轨迹
hold on
plot(tt*Ts,y_est(2,tt),'r','LineWidth',1); % 绘制DMK估计的半径轨迹
hold on
xlabel('t/s'); 
ylabel('r')
legend('含噪声测量信号','无噪声测量信号','扩散映射kalman滤波');



figure
scatter(tt*Ts,x1,20,[0.74,0.74,0.74],'.'); % 绘制噪声角度测量点
hold on
plot(tt*Ts,x0,'g:','LineWidth',2); % 绘制清洁角度轨迹
hold on
plot(tt*Ts,y_est(1,tt),'r','LineWidth',1); % 绘制DMK估计的角度轨迹
hold off;
xlabel('t/s');
ylabel('phi')
legend('含噪声测量信号','无噪声测量信号','扩散映射kalman滤波');
50

4.本算法原理

        基于梯度流的扩散映射卡尔曼滤波算法（Gradient Flow Diffusion Map Kalman Filter, GFDMKF）是一种将非线性流形学习理论与经典卡尔曼滤波相结合的信号处理方法，旨在提高对非线性、高维信号的滤波和跟踪性能。这种方法通过扩散映射（Diffusion Maps）捕捉数据的低维流形结构，随后利用梯度流（Gradient Flow）优化卡尔曼滤波的预测和更新步骤，从而在非线性动态系统中实现更精准的状态估计。

4.1 扩散映射（Diffusion Maps）

        扩散映射是一种非线性降维技术，通过构造一个扩散过程来揭示高维数据集的潜在低维流形结构。其核心是构造一个扩散核K(xi​,xj​)，通常选用高斯核：

4.2 卡尔曼滤波

4.3 基于梯度流的扩散映射卡尔曼滤波（GFDMKF）

       在GFDMKF中，首先应用扩散映射将原始高维状态空间映射到一个低维流形空间，从而简化卡尔曼滤波的计算复杂度。然后，利用梯度流优化映射空间中的状态预测和更新过程，以更好地适应非线性动态。

5.完整程序

VVV