相关题解
- 题目一:6291. 数组元素和与数字和的绝对差
- 题目二:6292. 子矩阵元素加 1
- 题目三:6293. 统计好子数组的数目
- 题目四:2538. 最大价值和与最小价值和的差值
题目一:6291. 数组元素和与数字和的绝对差
题目链接:
https://leetcode.cn/problems/difference-between-element-sum-and-digit-sum-of-an-array/
解题分析:
很简单的签到题啦,快速过
AC代码:
class Solution {
public:
int solve(int num)
{
int sum=0;
while(num)
{
sum+=num%10;
num/=10;
}
return sum;
}
int differenceOfSum(vector<int>& nums) {
int len=nums.size();
int sum1=0,sum2=0;
for(int i=0;i<len;i++)
{
sum1+=nums[i];
sum2+=solve(nums[i]);
}
return abs(sum1-sum2);
}
};
题目二:6292. 子矩阵元素加 1
题目链接:
https://leetcode.cn/problems/increment-submatrices-by-one/
解题分析:
二维差分,忘记了模板,比赛的时候现推,推了老半天,最好是能够直接记住
具体二维差分讲解间博客:https://blog.csdn.net/weixin_45629285/article/details/111146240
注意两个重要点:
- s[i][j]是以(i,j)为下标的左上角矩阵所有元素的和,也就是左上角为(0,0),右下角为(i,j)的矩阵
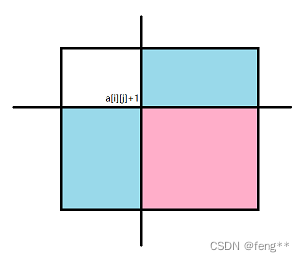
- a[i][j]加一,会使得以(i,j)为下标位置的右下角的矩阵所有的s都加一,也就是求和时包含a[i][j]这个元素的所有s加一,而不是二维数组遍历时经过a的那些位置的s加一,图中只有粉色位置的s值会加一,蓝色的不会
- 推二维差分的时候多多借鉴一维差分的思路,类比着推,一般a和s从下标1开始赋值比较好算
- vector数组在没有分配空间或者没有push_back值的时候不能使用下标进行访问和赋值,要么就用push_back来添加元素,要么就先resize,再用下标访问或赋值
AC代码:
class Solution {
public:
vector<vector<int>> rangeAddQueries(int n, vector<vector<int>>& queries) {
int a[n+1][n+1];
memset(a,0,sizeof(a));
int len=queries.size();
//cout<<queries[0][3]<<endl;
for(int i=0;i<len;i++)
{
int x1=queries[i][0],y1=queries[i][1],x2=queries[i][2],y2=queries[i][3];
a[x1][y1]+=1;
a[x1][y2+1]-=1;
a[x2+1][y1]-=1;
a[x2+1][y2+1]+=1;
}
vector<vector<int>>s(n+1);
for (int i = 0; i < s.size(); i++) s[i].resize(n+1);
vector<vector<int>>ans(n);
// s[0][0]=a[0][0];
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
s[i][j]=s[i][j-1]+s[i-1][j]-s[i-1][j-1]+a[i-1][j-1];
ans[i-1].push_back(s[i][j]);
}
}
return ans;
}
};
题目三:6293. 统计好子数组的数目
题目链接:
https://leetcode.cn/problems/count-the-number-of-good-subarrays/
解题分析:
- 首先看这个数据范围为1e5,要控制在O(nlogn)了,然后就是感觉是双指针就能做,虽然使用双指针要先经过严格的证明,证明当j往右走的时候i只能往右走,也就是二者成单调关系,但是有时候考虑一下模拟走的过程中会不会有什么问题,如果用双指针模拟没什么问题也就可以用了;双指针就是考虑清楚什么时候j往右走什么时候停下来,什么时候i往右走什么时候停下来就行,我个人喜欢每次while循环里只走一步,要么j走,要么i走,要么i和j都走一步,不喜欢在里面再写循环(一直走直到怎么怎么样)
- 这个题中,维护一个[i,j]区间,
当这个区间内的满足条件的对数还不够的时候j就需要不断往前走,直到对数够的时候当前[i,j]区间和剩下j右边的那些位置的数分别可以构成n-j个数组,更新数组个数
当这个区间内的满足条件的对数足够k个时,就可以让i往前走了,并且i往前走的过程中有左边的数字从区间中被淘汰出去,就需要更新一下区间内的对数
注意,一个区间中比如3可能出现多次,每两个3之间就能组成一对儿,因此要保存区间内每个数出现的次数,多纳入一个3时对数需要更新区间内3的个数那么多对
AC代码:
class Solution {
public:
map<int,int>exit; //存i,j区间里的数字及其个数
long long countGood(vector<int>& a, int k) {
int n=a.size();
int i=0,j=-1;
long long dui=0,sum=0;
while(j<n)
{
if(dui<k) //对数不够,j往前走
{
j++;
if(exit[a[j]]) //加入的数字在i,j区间里有
{
dui+=exit[a[j]]; //有几个对数就加几
}
exit[a[j]]++;
}
else //对数够,i往前走
{
if(dui>=k) sum+=n-j;
if(exit[a[i]]>=1)
{
dui-=exit[a[i]]-1; //i,j区间里还剩有该数字,剩下多少个对数就减少多少
}
exit[a[i]]--; //区间内个数减一
i++;
}
}
return sum;
}
};
题目四:2538. 最大价值和与最小价值和的差值
题目链接:
https://leetcode.cn/problems/difference-between-maximum-and-minimum-price-sum/
解题分析:
- 解法一:求树的直径,题目翻译过来其实就是找出树中所有的最长路径(树中最远的两个结点),然后求这些路径中权值和最大为多少,也就是求树的直径
具体的详细解答参考博客:
https://leetcode.cn/problems/difference-between-maximum-and-minimum-price-sum/solution/by-kpole-ces2/
求的时候可以用dfs也可以用bfs
AC代码:
class Solution {
public:
const static int N=100005;
int degree[N];
vector<int>adj[N]; //邻接表
//int visited[N];
long long Max=0,now=0,ans=0;
int max_e;
long long ds[N]; //s到每个点的距离
long long dt[N]; //t到每个点的距离
void dfs(int s,int fa,long long a[],vector<int>& price)
{
// cout<<now<<endl;
a[s]=now;
if(now>Max)
{
Max=now;
max_e=s;
}
for(int i=0;i<adj[s].size();i++)
{
if(adj[s][i]==fa) continue;
now+=price[adj[s][i]];
dfs(adj[s][i],s,a,price);
now-=price[adj[s][i]];
}
}
long long maxOutput(int n, vector<vector<int>>& edges, vector<int>& price) {
for(int i=0;i<edges.size();i++)
{
degree[edges[i][0]]++;
degree[edges[i][1]]++;
adj[edges[i][0]].push_back(edges[i][1]);
adj[edges[i][1]].push_back(edges[i][0]);
}
dfs(0,-1,ds,price);
int s=max_e;
now=price[s],Max=0;
dfs(s,-1,ds,price);
int t=max_e;
now=price[t],Max=0;
dfs(t,-1,dt,price);
for(int i=0;i<n;i++)
{
// cout<<ds[i]<<" ";
ans=max(ans,ds[i]-min(price[s],price[i]));
ans=max(ans,dt[i]-min(price[t],price[i]));
}
return ans;
}
};
- 解法二:DP解法