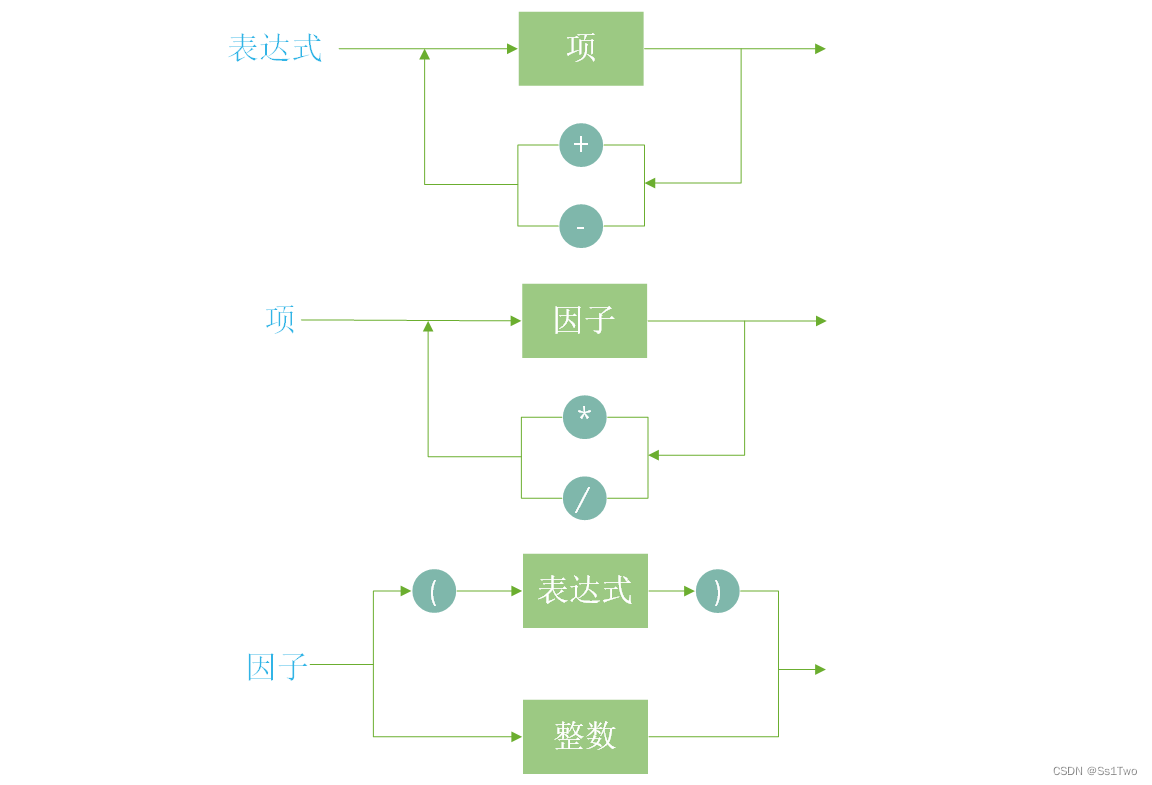
正交向量与子空间
本章研究的重点还是之前提到过的子空间,但是本章我们主要从正交的角度来探讨这些子空间具有的性质,主要内容见下图。
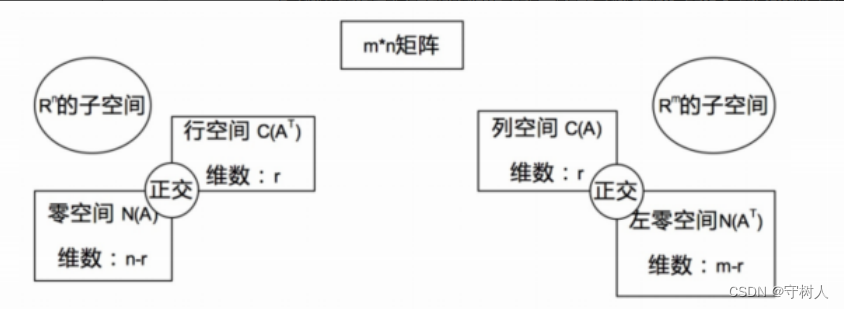
注意,上图指出了我们之前没有关注到的子空间的一些性质:对于一个矩阵,其零空间与行空间正交,其列空间与左零空间正交。
向量正交与空间正交
在线性代数中,正交就是垂直。无论我们讨论的是向量正交还是空间正交,都可以理解为垂直。
我们先研究最简单的向量正交:
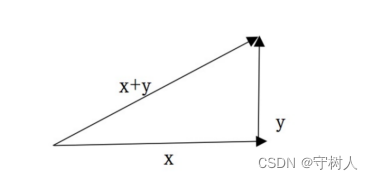
如上图,其中 与 向量之间相互垂直(正交)。根据垂直关系,可得 xTy =0,这是初高中的内容:如果两个向量相互垂直(正交),那么这两个向量的数量积(内积)为 。
如果两个向量中其中一个是零向量,则两个向量一定正交。
接下来我们讨论空间正交,两个空间正交意味着:其中一个空间中的任意一个向量,都与另外一个空间中的任意一个向量正交。
这里需要注意一种容易混淆的情况,比如以黑板和地板为例,这两者所处的空间并非是空间正交的,最直接的反例是黑板平面和地板平面的交线处,这个交线处上的向量既属于黑板平面,也属于地板平面,最简单地,取交线处上的向量的平方存在不为 0 的可能,所以黑板平与地板平面不是空间正交的。
这同时也提醒我们:两个平面若在非零向量处相交,则这两个平面一定是不正交的。
最后我们探究子空间中的正交情况,先简单地以 的子空间为例,R2的子空间有三种:整个平面D,过原点的直线 L,零向量。
就这三个子空间而言,显然L 和D 是不可能正交的,因为L 就在平面上,但L 和零向量,D 和零向量是正交的。此外, 和 之间也可能是正交的:两条直线需要在原点处互相垂直。
矩阵的子空间的正交情况
一个矩阵,其零空间与行空间是正交的,它们之间的关系类似于将一个空间一分为二所得到的两个子空间。
我们先证明为什么零空间和行空间是正交的,而这一点很容易从 Ax = 0上找到答案。
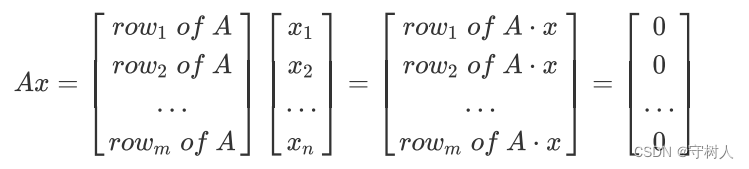
对于 ,有 Ax = 0的每一行与 相乘结果为零,这也即表明 A中的每一行与 x正交。 对应的是零空间中的任意向量,现 A中的每一行与x 相乘结果为零,那么显然A 中的行的线性组合与 x相乘结果依然为零,而 A中的行的线性组合对应的是行空间中的任意向量,所以,矩阵零空间与行空间正交。同样地,根据ATy = 0 ,我们能以相同的方法证明矩阵的列空间和左零空间是正交的。
无解方程Ax = b 的最优解
在上一课中我们看到了,矩阵的数据来源于实际测量,既然是测量,那么就存在测量不准确的情况,从而导致无解。此外,测量过程中极其细微的误差也可能导致无解。
除了测量因素以外,有时候 是一个长方形矩阵,其行数 很多,列数 很少(也即较少的未知数要满足非常多的方程),这时候有些方程得到的结果可能是有很大误差的,这个误差来自 ,也即 中有一部分是“坏数据”,这些“坏数据”使得方程无解。
我们可以不断去掉一些方程,用以剔除“坏数据”,最后得到一个可逆的方阵然后进行求解,但这种方法是不实际的,因为对于所有测量值而言,我们很难判断哪些是有效的好数据,哪些是无效的坏数据。一般我们希望利用所有的测量值求出“最优值”,类似于一种拟合
一种常用的方法是在方程两侧乘以 AT,无解方程从而改写成 
,求解新方程的解即为最优解。
注意,这个解并非是 A x= b 的解,我们已经假设 A x=b 是无解的,也即符合方程的x 不存在。在已知 Ax 不等于b的情况下,我们尝试求解 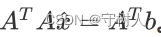
ATA未必是可逆的,当A的各列线性相关的时候,ATA就不可逆了。
- 性质一:N(ATA) = N(A):ATA与A的零空间相同。
- 性质二:rank(ATA) = rank(A):ATA与A的秩相同。
显然,如果 A的各列线性相关,那么A 的零空间就存在非零向量使得A 的各列线性组合为零向量。因为ATA 与A 的零空间相同,所以 ATA零空间就存在非零向量使得 ATA的各列线性组合为零向量,既然存在这样的非零向量,那么ATA 就不是一个可逆矩阵。