1.带环链表及其拓展
(1)这个题目组要就是进行判断这个链表是否带环,使用的是布尔类型作为返回值;
(2)我们这里的思路是使用的快慢指针,快指针一次走2步,慢指针一次走1步,如果这个过程中两个指针会相遇,那么我们就可以说明这个链表是带环的,否则就是不带环的;
(3)可能有些同学就会问,难道这个过程他们两个快慢指针就一定会相遇吗?这个当在快指针一次走两步的情况下,这个是一定会相遇的,为什么这么说呢?因为当慢指针进行环之后,每次快指针都会比慢指针多走一步,假设慢指针进入环的时候,两者之间的距离是L,每走一步,两者之间的距离就会减少一个单位长度,这个样的话,他们两个指针迟早是会相遇的;
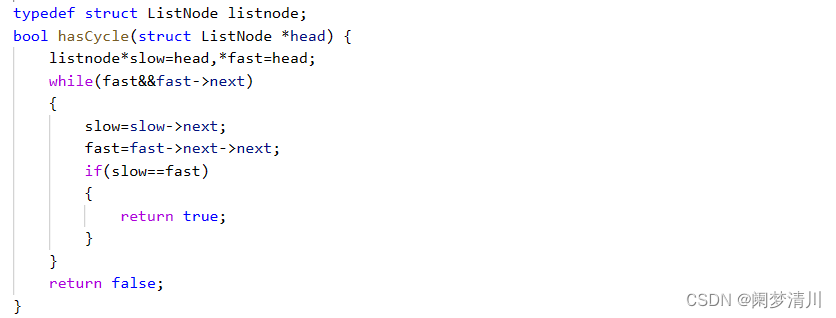
(4)这个题目本身可能并不是非常难,但是在这个题目的基础之上,面试官还会更加深入的进行提问:这个我们设计的快指针是一次走两个单位,如果一次走3个,一次走4个单位长度,又会是什么样的结果呢?
我们使用的判断依据就是一个快指针,一个慢指针,快指针先进入环(在有环的前提下面),慢指针后进入环,这个过程中快慢指针就会进行追击,是否一定可以追上呢?这个有何哪些因素相关呢?实际上这个和环上面的元素的个数以及初始情况下快慢指针的相差的个数有关;
(5)下面我们讨论一下当fast一次走3个单位长度的时候,会不会相遇,在什么情况下相遇?
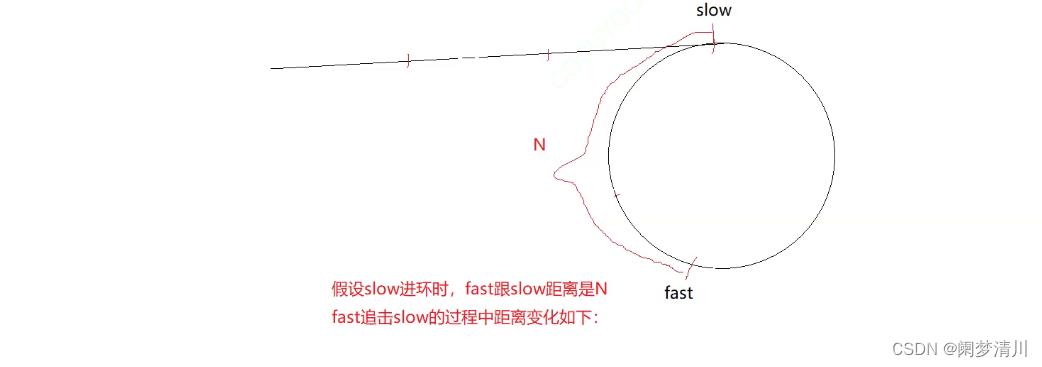
上面的就是一个基本的情况,我们的慢指针进入环的时候,快指针就已经在环里面走过很长的一段距离了,这个时候我们假设快指针和慢指针之间的距离是n,因为在这个情况线面我们的快指针是一次走3步,慢指针一次走1步,这个时候,我们的快指针每次都会比慢指针多走2步,每次都是两步两步的进行追击,我们在这个情况下面能不能追上就和n的救星有关了;
因为如果这个n是偶数,每次快指针都比慢指针多走两步,那么最后一定是可以追上的,但是如果n是奇数,每次减少2个单位长度,最后就是相差的5,3,1相差到1个单位长度的时候,我们的快指针已经马上可以追上慢指针了,但是因为快指针每次都会比慢指针多走2步,这个时候就会错过,出现的结果就是快指针跑到了慢指针的前面,之后他们的差距就会增加,展开新一轮的追击;
到这个时候,你千万不要以为两个错过之后就结束了,就再也不会相遇了,因为这个时候快指针还是走得快,这个一段时间之后他们两个还是会相遇的,这个情况我们还是要继续进行分析的;
这个时候我们定义一个新的变量就是C,这个C代表的就是环上面的元素的个数,或者说是节点的个数,因为当快指针还差一个单位长度追上慢指针的时候,就会出现快指针一次比慢指针走2步,从而实现超越,这个时候两者之间相差的元素的个数就是n-1了,这个时候展开新一轮的追击,每次快指针还是比慢指针多走两步,当这个n-1是偶数,也就是说n是奇数的时候,两步两步的进行追击,最后是可以追上的,但是当n-1还是奇数的时候,就会出现又会错过的情况,这个时候之后就永远都不会追上了(因为最后的时候还是马上就要追上的时候实现超越,两者之间还是相差n-1个元素);
(6)针对上面的分析,我们进行总结一下:当快指针一次走3步的时候,就会因为两个之间相差的元素的个数出现不同的情况,
一种就是n是偶数,这样的话两步两步的追最后就可以追上了;
但是当n是奇数的时候,我们就要重新对于情况进行划分:我们重新定义c作为这个环上面的元素的个数,当c-1是偶数的时候,第二轮可以追上的,但是当c-1是奇数的时候,最后就永远追不上了;
总的来讲:n是奇数,c是偶数的时候,就会永远追不上;
(7)当快指针一次走4步,我们快指针每次都比慢指针多走3个单位长度,我们就要判断这个之间的元素n的情况,我们这个时候就不是按照奇偶性进行讨论,而是看这个n和3之间的关系,从而进行对应的判断,这里只会更加复杂,但是分析的方法同上,这里不再赘述,感兴趣的小伙伴可自行进行讨论;
(8)永远追不上的条件分析:我们以快指针一次走3步作为例子,我们通过这个快指针的路程是慢指针的3被作为等量关系列式
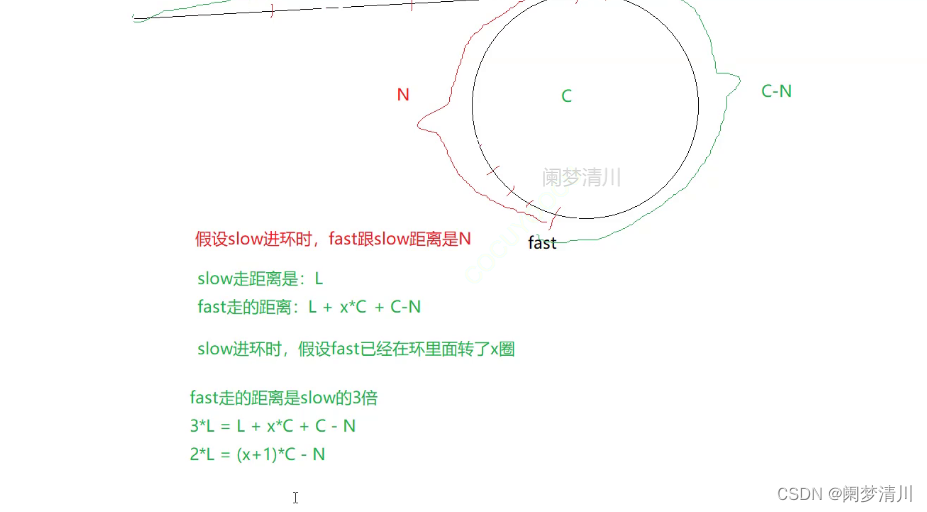
上面的就是我们进行分析的过程:n还是慢指针进环的时候,快慢指针之间相差的元素个数,L指的是进环之前的路程,我们分别表示出来开始到慢指针进环快慢指针走过的路程,利用之间的3被作为等量关系列示求解;
上面我们是以慢指针进环的时候两者之间的3被关系作为关系的,实际上这个过程中快指针始终是慢指针的3被,我们只是选取了慢指针进入环的这个时刻进行分析罢了;
慢指针走的路程就是L,我们假设fast在慢指针进入环之前就已经走了x圈,这个时候我们表示出来快指针走过的路程,利用3倍关系进行计算,最后的出来这个等式2*L=(x+1)*C-n;
我们上面就已经讨论过,n是奇数,C是偶数的时候永远不会相遇,我们带入就可以发现,2*L肯定是奇数,因为C是奇数(x+1)*C肯定是偶数,偶数-n是偶数,当n是奇数的时候这个等式肯定是不成立的,所以我们发现,我们上面讨论的那个永远不会相遇的情况是不满足这个等式的。
(9)这个时候,你还清醒吗?就是我们通过理论的分析,发现当n是奇数,c是偶数的时候,就会永远错过;
但是我们的快慢指针走的路程满足3倍关系,我们推理出来一个等式,我们的n奇数,c偶数根本不会满足这个等式,就说明我们的n奇数c偶数根本就不存在,因此这个当快指针一次走3个单位长度的时候,不会出现永远错过的情况,一定会相遇,这个就是我们通过上面的严谨的证明过程想要得出的结论。