强化训练：day9（添加逗号、跳台阶、扑克牌顺子）

news2024/11/20 11:34:07

文章目录

前言
1. 添加逗号
- 1.1 题目描述
- 2.2 解题思路
- 2.3 代码实现
2. 跳台阶
- 2.1 题目描述
- 2.2 解题思路
- 2.3 代码实现
3. 扑克牌顺子
- 3.1 题目描述
- 3.2 解题思路
- 3.3 代码实现
总结

前言

1. 添加逗号
2. 跳台阶
3. 扑克牌顺子

1. 添加逗号

1.1 题目描述

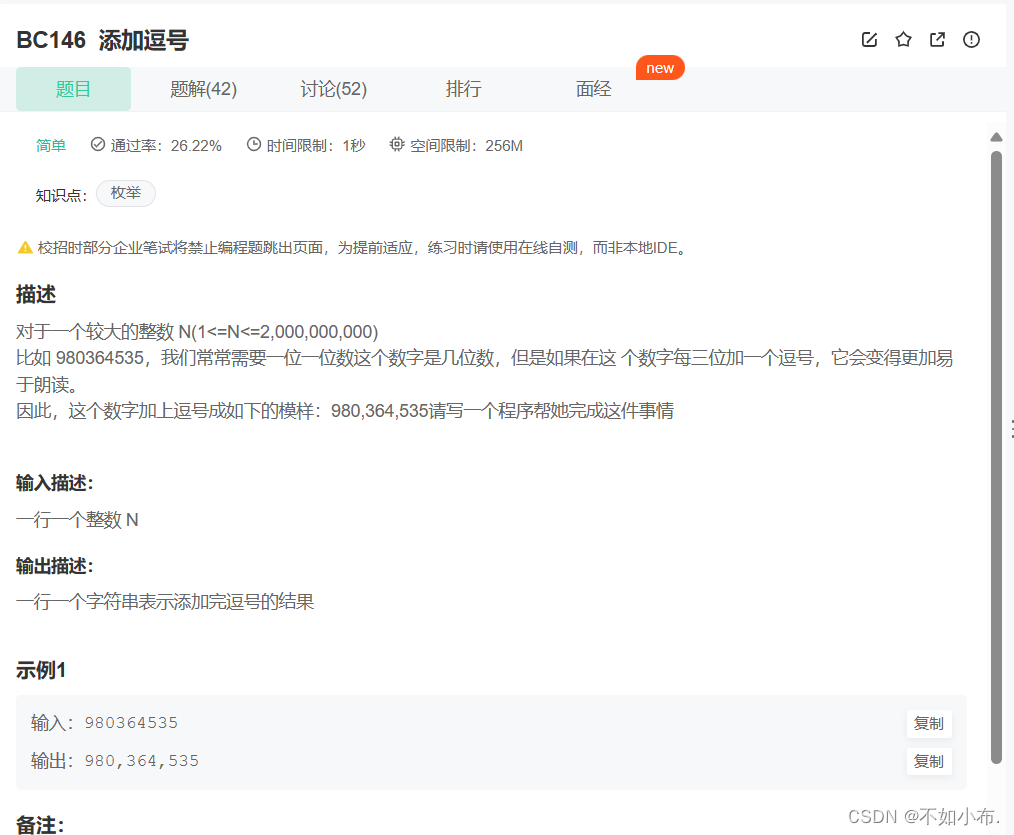
在这里插入图片描述

2.2 解题思路

我的写法是先进行逆置，然后再创建一个字符串，然后一个一个添加上去，每添加三个字符，就加上一个逗号，结束之后再进行逆置就可以了。（当然也可以直接逆序遍历，这样就不需要逆置了）

2.3 代码实现

#include <iostream>
using namespace std;
#include <string>
#include <algorithm>
int main() 
{
    string ret, num;
    cin >> num;
    reverse(num.begin(), num.end());
    int n = num.size();
    int k = 0;
    while (k < n) 
    {
        if (k != 0 && k % 3 == 0)
            ret += ",";
        ret += num[k++];
    }
    reverse(ret.begin(), ret.end());
    cout << ret;
    return 0;
}

2. 跳台阶

2.1 题目描述

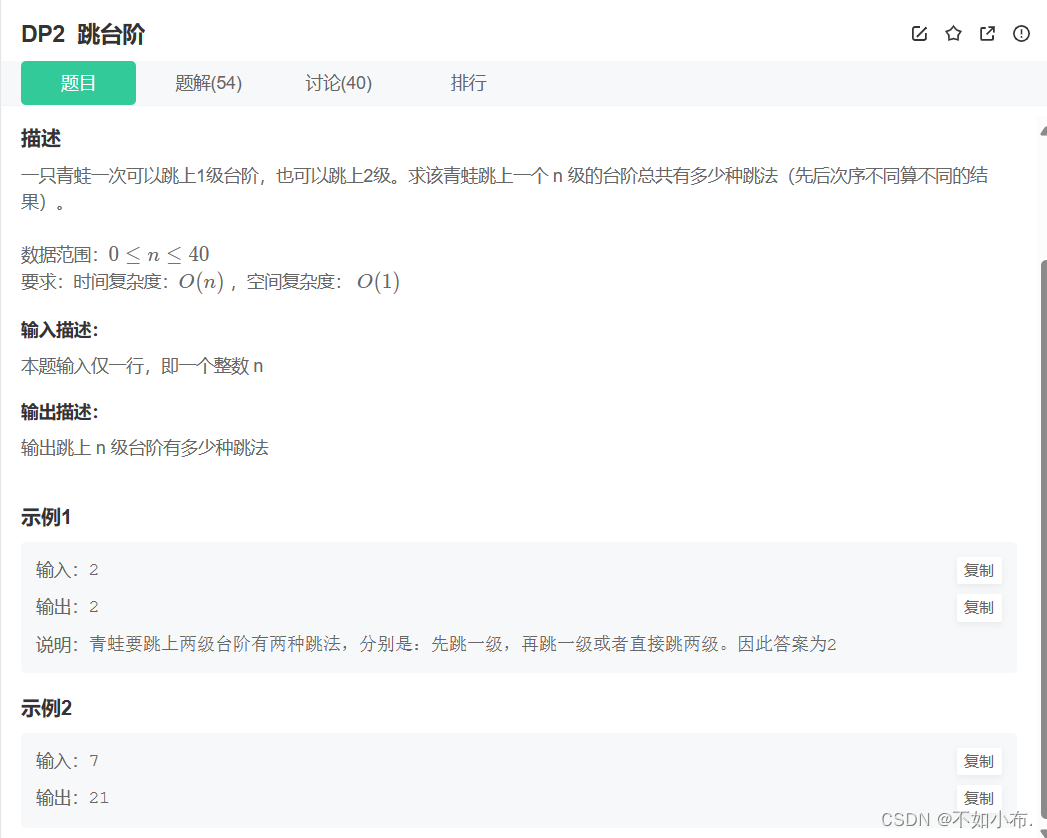
在这里插入图片描述

2.2 解题思路

还是一道简单的dp问题，大概思路与之前写的最小花费爬楼梯相差无几。
状态表示：dp[i] -> 到达 i 位置一共有多少跳法。每一个位置的跳法都来源于它前两个台阶，所以状态转移方程就是：dp[i] = dp[i-1] + dp[i-2]。
还可以进行优化，那就是只用两个变量来保存一个台阶前两个台阶的各自的跳法，就像滚动数组一样，不断向前就可以了。如果不理解就写成上面的状态转移方程就行了。

2.3 代码实现

#include <iostream>
using namespace std;
int main() {
    int n = 0;
    cin >> n;
    int dp1 = 1, dp2 = 2;
    int ret = 0;
    if (n == 1) ret = 1;
    else if (n == 2) ret = 2;
    else 
    {
        for (int i = 3; i <= n; i++) 
        {
            ret = dp1 + dp2;
            dp1 = dp2;
            dp2 = ret;
        }
    }
    cout << ret;
    return 0;
}

3. 扑克牌顺子

3.1 题目描述

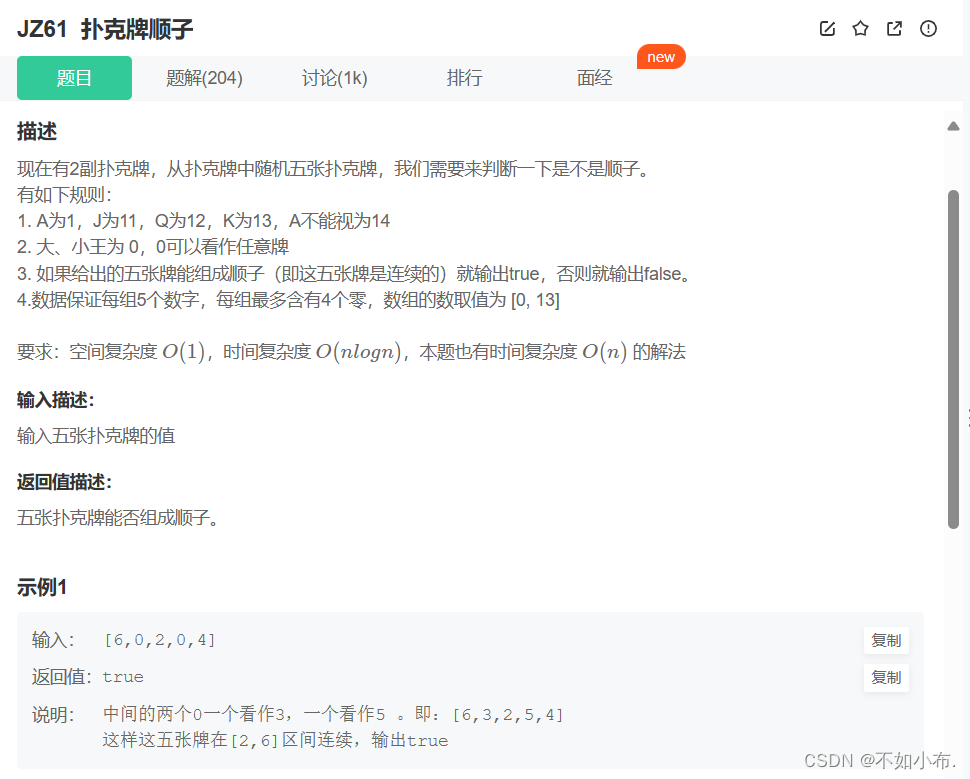
在这里插入图片描述

3.2 解题思路

一开始我想了很多，写了半天写不出来，最后一看题解……
其实这道题很简单，我们只要发现其中的规则，一下就出来了，那就是：最大的牌数和最小的牌数只差应该是等于4的（1，2，3，4，5），但是还有可能出现0的情况（3，4，5，0，0），因此所得的五张牌的最大与最小只差应该是小于等于4。但是其中不能有重复的牌（0可以重复噢），所以还需要判断（哈希）。
我们只需要遍历一遍数组，找出最大与最小，看看它们的差值是否小于等于4就可以了，同时如果出现重复数字之间返回false即可。

3.3 代码实现

class Solution {
public:
    bool hash[14];
    bool IsContinuous(vector<int>& nums) 
    {
        memset(hash, 0, sizeof hash);
        int maxVal = 0, minVal = 14;
        for(auto x : nums)
        {
            if(x)
            {
                if(hash[x]) return false;
                else
                {
                    hash[x] = true;
                    maxVal = max(maxVal, x);                
                    minVal = min(minVal, x);                
                }
            }
        }
        return maxVal - minVal <= 4;
    }
};