T1. 龟兔赛跑

题目描述

兔子又来找乌龟赛跑啦！同样的错误兔子不会犯两次，所以兔子提出赛跑的时候，乌龟就觉得这场比赛很不公平。于是兔子进一步放宽了条件，表示他可以在比赛开始以后先睡 $t$ 分钟再开始追乌龟。

乌龟这下没办法确定比赛到底公平不公平了，所以请你来帮忙。假设乌龟每分钟可以跑 $x$ 米，兔子每分钟跑 $y$ 米 $(x<y)$。他希望你计算最大的整数赛跑距离 (米)，满足乌龟能在兔子先睡 $t$ 分钟的前提下，比兔子更早或同时到达终点。

输入格式

三个整数 $x,y,t$。

输出格式

一个整数，表示要求的最长赛跑距离。

样例 #1

样例输入 #1

11 21 7

样例输出 #1

161

提示

$1\le x<y\le 100,t\le 1000$。

本题原始满分为 $15\text{pts}$。

正解

简单的追及问题，答案是 $x\times t+1.0\times x\times t÷(y-x)\times x$。

代码

#include <bits/stdc++.h>
using namespace std;
int x,y,t; 
int main()
{
	cin >> x >> y >> t;
	cout << int(x * t + 1.0 * x * t / (y - x) * x);
	return 0;
}

T2. 基因组分析

题目描述

乌龟得到了他的基因组，一个只包含 $\mathtt{ATCG}$ 四种字母的字符串。乌龟想起科学家说，基因组中很多片段都多次重复出现，而且这种重复是很有意义的，于是他想计算一下自己基因组里片段的重复情况。

给定一个基因组，其中一个长度为 $k$ 的子串称为一个“$k$-片段”。乌龟希望你计算出基因组中不同的 $k$-片段数量。例如，基因组 $\mathtt{TACAC}$ 的 $2$-片段有 $\mathtt{TA},\mathtt{AC},\mathtt{CA},\mathtt{AC}$，其中不同的片段数量有 $3$ 个。

---

试题中使用的生成数列 $R$ 定义如下：整数 $0\le R_1<201701$ 在输入中给出。

对于 $i>1,R_i=(R_{i-1}\times 6807+2831)\mathrm{mod}201701$。

输入格式

整数 $n,k,R_1$，表示基因组的长度、片段的长度和数列生成的首项。基因组第 $i(1\le i\le n)$ 个字符在 $R_i\mathrm{mod}4$ 的值为 $0,1,2,3$ 时分别为 $\mathtt{A},\mathtt{T},\mathtt{C},\mathtt{G}$。

输出格式

一个整数，表示不同的 $k$-片段的数量。

样例 #1

样例输入 #1

20 2 37

样例输出 #1

10

提示

$30\%$ 的数据满足 $n\le 100$；

$100\%$ 的数据满足 $1\le n\le 10^5,1\le k\le 10$。

本题原始满分为 $20\text{pts}$。

正解

直接根据题意暴力枚举即可，时间复杂度为 $O(nm)$，不会超。

代码

#include <bits/stdc++.h>
#define int long long
using namespace std;

int a,b,c;
string s = "ATCG";
map <string,int> mp;
string t;
int sum;

void solve()
{
	cin >> a >> b >> c;
	for (int i = 0;i < a;i++)
		t += s[c%4],c = (c*6807+2831) % 201701;
	for (int i = 0;i < a-b+1;i++)
	{
		string n = "";
		for (int j = i;j <= i+b-1;j++)
			n += t[j];
		if (mp[n] != 1)
			mp[n] = 1,sum++;
	}
	cout << sum;
}

signed main()
{
	int TTT;
//	cin >> TTT;
	TTT = 1;
	while (TTT--) solve();
	return 0;
}

T3. 任务调度

题目描述

乌龟因为动作太慢，有 $n$ 个任务已经超过截止日期了。乌龟处理第 $i$ 个任务需要 $a_i$ 单位时间。从 $0$ 时刻开始，乌龟可以选择某项任务，完成它，然后再开始另一项任务，如此往复直到所有任务都被完成。

由于已经超过截止日期，乌龟会为此受到一定的惩罚，惩罚值等于所有任务完成时刻之和。例如，有 2 个任务分别需要 $10$ 和 $20$ 单位时间完成。如果先完成任务 1，惩罚值为 $10+30=40$；如果先完成任务 2，惩罚值为 $20+30=50$。

乌龟希望你求出惩罚值最小的完成任务的顺序。

---

试题中使用的生成数列 $R$ 定义如下：整数 $0\le R_1<201701$ 在输入中给出。

对于 $i>1,R_i=(R_{i-1}\times 6807+2831)\mathrm{mod}201701$。

输入格式

两个整数 $n,R_1$，表示任务的数量和生成数列的首项。处理任务 $i(1\le i\le n)$ 的时间 $a_i=(R_i\mathrm{mod}100)+1$。

输出格式

一个整数，表示完成所有任务的最小惩罚值。

样例 #1

样例输入 #1

10 2

样例输出 #1

1641

提示

对于 $100\%$ 的数据，$1\le n\le 10^3$。

本题原始满分为 $15\text{pts}$。

正解

直接根据题意模拟即可。

代码

#include <bits/stdc++.h>
#define int long long
using namespace std;

int n,m;
int a[1010],b[1010];

void solve()
{
	cin >> n >> m;
	b[1] = m;
	for (int i = 2;i <= n;i++)
		b[i] = (b[i-1]*6807+2831) % 201701;
	for (int i = 1;i <= n;i++)
		a[i] = b[i] % 100 + 1;
	sort(a+1,a+n+1);
	int ans = 0,sum = 0;
	for (int i = 1;i <= n;i++)
		sum += a[i],ans += sum;
	cout << ans;
}

signed main()
{
	int TTT;
//	cin >> TTT;
	TTT = 1;
	while (TTT--) solve();
	return 0;
}

T4. 密码锁

题目描述

乌龟给自己的贵重物品上了密码锁。密码锁上有 $5$ 个数字拨盘。每个数字拨盘每次向上拨使数字增加 $1$ （$9$ 向上拨得到 $0$），向下拨使数字减少 $1$ （$0$ 向下拨得到 $9$）。

拨盘上的数字组成一个 $5$ 位数。只要拨盘上的数字变为素数，密码锁就会被解开。素数 (又称质数) 是只能被 $1$ 和它自身整除的大于 $1$ 的自然数。因为乌龟动作实在太慢，他希望你帮他计算如何开锁，使得拨动的总次数最少。

输入格式

一个 $5$ 位数，表示拨盘的初始数字。

输出格式

一个 $5$ 位素数，表示开启密码锁使用的素数（拨动次数最少）。如有多组解，输出满足条件的最大数。

样例 #1

样例输入 #1

01210

样例输出 #1

01319

提示

本题原始满分为 $15\text{pts}$。

正解

根据题意模拟即可。

代码

#include <bits/stdc++.h>
#define int long long
using namespace std;

int n,ans,mi = 1e18,idx;
int check(int x)
{
	if (x == 1) return 0;
	for (int i = 2;i * i <= x;i++)
		if (x % i == 0)
			return 0;
	return 1;
}

void solve()
{
	cin >> n;
	int na = n / 10000,nb = n / 1000 % 10,nc = n / 100 % 10,nd = n / 10 % 10,ne = n % 10;
	for (int i = 2;i <= 99999;i++)
		if (check(i))
		{
			int ia = i / 10000,ib = i / 1000 % 10,ic = i / 100 % 10,id = i / 10 % 10,ie = i % 10;
			ans += min((na-ia+10)%10,(ia-na+10)%10);
			ans += min((nb-ib+10)%10,(ib-nb+10)%10);
			ans += min((nc-ic+10)%10,(ic-nc+10)%10);
			ans += min((nd-id+10)%10,(id-nd+10)%10);
			ans += min((ne-ie+10)%10,(ie-ne+10)%10);
			if (mi > ans) mi = ans,idx = i;
			else if (mi == ans && idx < i) idx = i;
			ans = 0;
		}
	if (idx < 10000) cout << 0;
	if (idx < 1000) cout << 0;
	if (idx < 100) cout << 0;
	if (idx < 10) cout << 0;
	cout << idx;
}

signed main()
{
	int TTT;
//	cin >> TTT;
	TTT = 1;
	while (TTT--) solve();
	return 0;
}

T5. 房屋积水

题目描述

乌龟家的屋顶是凹凸不平的，所以每次雨后都会积水。为了知道屋顶是否会在暴雨后塌掉，他把屋顶的形状给了你，希望你帮他计算暴雨后屋顶的积水总量。

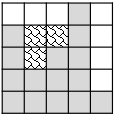
乌龟的屋顶由顺次排在同一水平线上的 $n$ 个宽度为 $1$、高度为整数 (分别给出) 的瓦片组成。例如给定 $n=5$，瓦片的高度分别为 $4,2,3,5,1$，屋顶可以画在下图所示的网格中，灰色格子为瓦片。

暴雨过后，如果一个方格向左右两侧延伸都能到达瓦片占据的方格，它就会积水。所以图中波浪线格子在暴雨后会积水，屋顶的积水方格总数为 $3$。

---

试题中使用的生成数列 $R$ 定义如下：整数 $0\le R_1<201701$ 在输入中给出。

对于 $i>1,R_i=(R_{i-1}\times 6807+2831)\mathrm{mod}201701$。

输入格式

两个整数 $n,R_1$，表示屋顶的宽度和生成数列的首项。从左向右数第 $i(1\le i\le n)$ 个瓦片的高度 $a_i=R_i\mathrm{mod}10$。

输出格式

一个整数，表示暴雨后屋顶积水方格的总数。

样例 #1

样例输入 #1

10 1

样例输出 #1

23

提示

$1\le n\le 100$。

本题原始满分为 $15\text{pts}$。

正解

通过正序房屋的最大值、倒序房屋的最大值，来求出中间部分的数量。

代码

#include <bits/stdc++.h>
#define int long long
using namespace std;

int n,sum;
int a[111],b[111],c[111],r[111];

void solve()
{
	cin >> n >> r[1];
	for (int i = 2;i <= n;i++)
		r[i] = (r[i-1]*6807+2831) % 201701;
	for (int i = 1;i <= n;i++)
		a[i] = r[i] % 10;
	for (int i = 1;i <= n;i++)
		b[i] = max(b[i-1],a[i]);
	for (int i = n;i >= 1;i--)
		c[i] = max(c[i+1],a[i]);
	for (int i = 1;i <= n;i++)
		sum += min(b[i],c[i]) - a[i];
	cout << sum;
}

signed main()
{
	int TTT;
//	cin >> TTT;
	TTT = 1;
	while (TTT--) solve();
	return 0;
}