发现宝藏

前些天发现了一个巨牛的人工智能学习网站，通俗易懂，风趣幽默，忍不住分享一下给大家。【宝藏入口】。

---

第十一届蓝桥杯大赛软件类决赛 Java C 组

【考生须知】

考试开始后, 选手首先下载题目, 并使用考场现场公布的解压密码解压试

考试时间为 4 小时。考试期间选手可汶览自己已经提交的答案, 被浏览的答案允许拷贝。时间截止后, 将无法继续提交或浏览答案。

对同一题目, 选手可多次提交答案, 以最后一次提交的答案为准。

选手必须通过浏览器方式提交自己的答案。选手在其它位置的作答或其它方式提交的答案无效。

试题包含 “结果填空” 和 “程序设计” 两种题型。

结果填空题: 要求选手根据题目描述直接填写结果。求解方式不限。不要求源代码。把结果填空的答案直接通过网页提交即可, 不要书写多余的内容。

程序设计题: 要求选手设计的程序对于给定的输入能给出正确的输出结果。考生的程序只有能运行出正确结果才有机会得分。

注意: 在评卷时使用的输入数据与试卷中给出的示例数据可能是不同的。选手的程序必须是通用的, 不能只对试卷中给定的数据有效。

所有源码必须在同一文件中。调试通过后，拷贝提交。

注意: 不要使用 package 语句。

注意: 选手代码的主类名必须为: Main, 否则会被判为无效代码。

注意: 如果程序中引用了类库, 在提交时必须将 import 语句与程序的其他部分同时提交。只允许使用 Java 自带的类库。

---

试题 A: 美丽的 2

本题总分: 5 分

【问题描述】

小蓝特别喜欢 2 , 今年是公元 2020 年, 他特别高兴。

他很好奇, 在公元 1 年到公元 2020 年 (包含) 中, 有多少个年份的数位中包含数字 2 ?

【答案提交】

这是一道结果填空的题, 你只需要算出结果后提交即可。本题的结果为一个整数, 在提交答案时只填写这个整数, 填写多余的内容将无法得分。

---

试题 B: 合数个数

本题总分: 5 分

【问题描述】

一个数如果除了 1 和自己还有其他约数, 则称为一个合数。例如: $1,2,3$不是合数, 4,6 是合数。

请问从 1 到 2020 一共有多少个合数。

【答案提交】

这是一道结果填空的题, 你只需要算出结果后提交即可。本题的结果为一个整数, 在提交答案时只填写这个整数, 填写多余的内容将无法得分。

---

试题 C: 扩散

本题总分: 10 分

【问题描述】

小蓝在一张无限大的特殊画布上作画。

这张画布可以看成一个方格图, 每个格子可以用一个二维的整数坐标表示。

小蓝在画布上首先点了一下几个点: $(0,0),(2020,11),(11,14),(2000,2000)$ 。只有这几个格子上有黑色, 其它位置都是白色的。

每过一分钟, 黑色就会扩散一点。具体的, 如果一个格子里面是黑色, 它就会扩散到上、下、左、右四个相邻的格子中, 使得这四个格子也变成黑色 (如果原来就是黑色, 则还是黑色)。

请问, 经过 2020 分钟后，画布上有多少个格子是黑色的。

【答案提交】

这是一道结果填空的题, 你只需要算出结果后提交即可。本题的结果为一个整数, 在提交答案时只填写这个整数, 填写多余的内容将无法得分。

---

试题 D: 阶乘约数

本题总分: 10 分

【问题描述】

定义阶乘 $n!=1\times 2\times 3\times \cdots \times n$ 。

请问 $100!（100$ 的阶乘）有多少个正约数。

【答案提交】

这是一道结果填空的题, 你只需要算出结果后提交即可。本题的结果为一个整数, 在提交答案时只填写这个整数, 填写多余的内容将无法得分。

---

试题 E: 本质上升序列

本题总分: 15 分

小蓝特别喜欢单调递增的事物。

在一个字符串中, 如果取出若干个字符, 将这些字符按照在字符串中的顺序排列后是单调递增的, 则成为这个字符串中的一个单调递增子序列。

例如, 在字符串 lanqiao 中, 如果取出字符 $n$ 和 $q$, 则 $nq$ 组成一个单调递增子序列。类似的单调递增子序列还有 $1\mathrm{nq}$ 、 i、ano 等等。

小蓝发现, 有些子序列虽然位置不同, 但是字符序列是一样的, 例如取第二个字符和最后一个字符可以取到 ao, 取最后两个字符也可以取到 ao。小蓝认为他们并没有本质不同。

对于一个字符串, 小蓝想知道, 本质不同的递增子序列有多少个?

例如, 对于字符串 lanqiao, 本质不同的递增子序列有 21 个。它们分别是 $1、a、n、q、i、o、1n、an、1q、aq、nq、ai、1o、ao、no、iov1nq、$ anq, Ino, ano, aio.

请问对于以下字符串 (共 200 个小写英文字母, 分四行显示)： (如果你把以下文字复制到文本文件中, 请务必检查复制的内容是否与文档中的一致。在试题目录下有一个文件 inc.txt, 内容与下面的文本相同)

tocyjkdzcieoiodfpbgcncsrjbhmugdnojjddhllnofawllbhf iadgdcdjstemphmnjihecoapdjjrprrqnhgccevdarufmliqij gihhfgdemxvicfauachlifhafpdccfseflcdgjncadfclvfmad vrnaaahahndsikzssoywakgnfjjaihtniptwoulxbaeqkqhfwl

本质不同的递增子序列有多少个?

【答案提交】

这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数, 在提交答案时只填写这个整数, 填写多余的内容将无法得分。

---

试题 F 天干地支

时间限制: $1.0\mathrm{s}$ 内存限制: $512.0\mathrm{MB}$ 本题总分: 15 分

【问题描述】

古代中国使用天干地支来记录当前的年份。

天干一共有十个, 分别为: 甲 (jiǎ)、乙 (yǐ)、丙 (bǐng)、丁 (dīng)、戊 (wù)、己 (ji)、庚 (gēng)、辛 (xīn)、壬 (rén)、癸 (guǐ)。

地支一共有十二个, 分别为：子（ž）、丑（chǒu）、寅（yín）、卯（mǎo）、辰 (chén)、巳 (sì)、午（wǔ）、未（wèi）、申（shēn）、西（yǒu）、戌（xū）、亥 (hài)。

将天干和地支连起来, 就组成了一个天干地支的年份, 例如: 甲子。 2020 年是庚子年。

每过一年, 天干和地支都会移动到下一个。例如 2021 年是辛丑年。

每过 60 年, 天干会循环 6 轮, 地支会循环 5 轮, 所以天干地支纪年每 60 年轮回一次。例如 1900 年, 1960 年, 2020 年都是庚子年。

给定一个公元纪年的年份, 请输出这一年的天干地支年份。

【输入格式】

输入一行包含一个正整数, 表示公元年份。

【输出格式】

输出一个拼音, 表示天干地支的年份, 天干和地支都用小写拼音表示（不表示声调)，之间不要加入任何多余的字符。

【样例输入】

$\begin{array}{l}2020\end{array}$

【样例输出】

$\begin{array}{l}gengzi\end{array}$

【评测用例规模与约定】

对于所有评测用例, 输入的公元年份为不超过 9999 的正整数。

---

试题 G 皮亚诺曲线距离

时间限制: $1.0\mathrm{s}$ 内存限制: $512.0\mathrm{MB}$ 本题总分: 20 分

---

【问题描述】

皮亚诺曲线是一条平面内的曲线。

下图给出了皮亚诺曲线的 1 阶情形, 它是从左下角出发, 经过一个 $3\times 3$ 的方格中的每一个格子, 最终到达右上角的一条曲线。

下图给出了皮亚诺曲线的 2 阶情形, 它是经过一个 $3^2\times 3^2$ 的方格中的每一个格子的一条曲线。它是将 1 阶曲线的每个方格由 1 阶曲线替换而成。

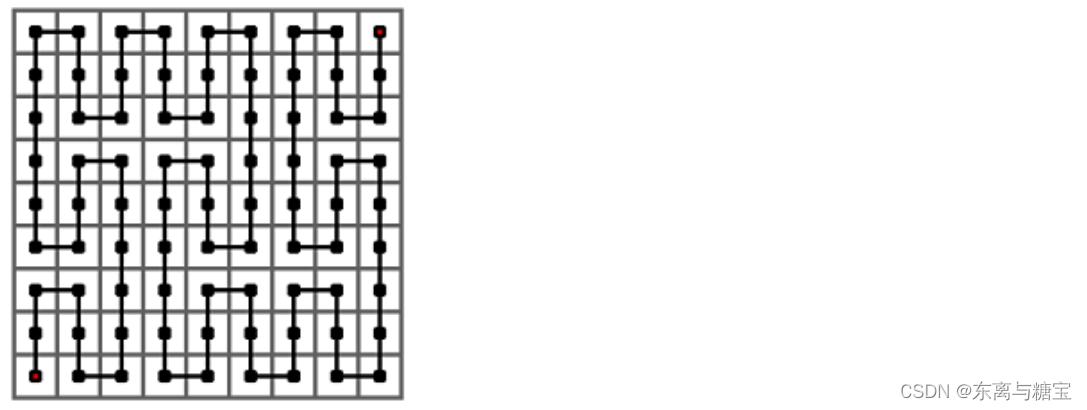
下图给出了皮亚诺曲线的 3 阶情形, 它是经过一个 $3^3\times 3^3$ 的方格中的每一个格子的一条曲线。它是将 2 阶曲线的每个方格由 1 阶曲线替换而成。

皮亚诺曲线总是从左下角开始出发, 最终到达右上角。

我们将这些格子放到坐标系中, 对于 $k$ 阶皮亚诺曲线, 左下角的坐标是 $(0,0)$, 右上角坐标是 $\left(3^k-1,3^k-1\right)$, 右下角坐标是 $\left(3^k-1,0\right)$, 左上角坐标是 $\left(0,3^k-1\right)$ 。

给定 $k$ 阶皮亚诺曲线上的两个点的坐标, 请问这两个点之间, 如果沿着皮亚诺曲线走, 距离是到少?

【输入格式】

输入的第一行包含一个正整数 $k$, 皮亚诺曲线的阶数。
第二行包含两个整数 $x_1,y_1$, 表示第一个点的坐标。
第三行包含两个整数 $x_2,y_2$, 表示第二个点的坐标。

【输出格式】

输出一个整数, 表示给定的两个点之间的距离。

【样例输入】

$\begin{array}{l}1\end{array}$

$\begin{array}{ll}0& 0\end{array}$

$\begin{array}{ll}2& 2\end{array}$

【样例输出】

$\begin{array}{l}8\end{array}$

【样例输入】

$\begin{array}{l}2\end{array}$

$\begin{array}{ll}0& 2\end{array}$

$\begin{array}{ll}0& 3\end{array}$

【样例输出】

$\begin{array}{l}13\end{array}$

【评测用例规模与约定】
对于 $30\%$ 的评测用例， $0\le k\le 10$ 。
对于 $50\%$ 的评测用例， $0\le k\le 20$ 。
对于所有评测用例, $0\le k\le 100,0\le x_1,y_1,x_2,y_2<3^k,x_1,y_1,x_2,y_2\le 10^{18}$ 。数据保证答案不超过 $10^{18}$ 。

---

试题 H 蓝肽子序列

时间限制: $1.0\mathrm{s}$ 内存限制: $512.0\mathrm{MB}$ 本题总分: 20 分

---

【问题描述】

$\mathrm{L}$ 星球上的生物由蛋蓝质组成, 每一种㞼蓝质由一类称为蓝肽的物资首尼连接成一条长链后折叠而成。

生物学家小乔正在研究 L 星球上的蛋蓝质。她拿到两个蛋蓝质的蓝肽序列,想通过这两条蓝肽序列的共同特点来分析两种蛋蓝质的相似性。

具体的, 一个蓝肽可以使用 1 至 5 个英文字母母表示, 其中第一个字母大写,后面的字母小写。一个蛋蓝质的蓝肚序列可以用蓝肚的表示顺序拼接而成。

在一条蓝肽序列中, 如果选取其中的一些位置, 把这些位置的蓝朋取出,并按照它们在原序列中的位置摆放, 则称为这条蓝肽的一个子序列。蓝肽的子序列不一定在原序列中是连续的, 中间可能间隔着一些未被取出的蓝肽。

如果第一条蓝肽序列可以取出一个子序列与第二条蓝肽序列中取出的某个子序列相等, 则称为一个公共蓝肚子序列。

给定两条蓝肽序列, 找出他们最长的那个公共蓝肚子序列的长度。

【输入格式】

输入两行, 每行包含一个字符串, 表示一个蓝肚序列。字符串中间没有空格等分隔字符。

【输出格式】

输出一个整数, 表示最长的那个公共蓝肚子序列的长度。

【样例输入】

$\begin{array}{l}LanQiaoBei\end{array}$

$\begin{array}{l}LanTaiXiaoQiao\end{array}$

【样例输出】

$\begin{array}{l}2\end{array}$

【样例说明】

最长的公共蓝肽子序列为 LanQiao, 共两个蓝肚。

【评测用例规模与约定】

对于 $20\%$ 的评测用例, 两个字符串的长度均不超过 20 。

对于 $50\%$ 的评测用例, 两个字符串的长度均不超过 100 。

对于所有评测用例, 两个字符串的长度均不超过 1000。

试题 I: 画廊

时间限制: $1.0\mathrm{s}$ 内存限制: $512.0\mathrm{MB}$ 本题总分: 25 分

【问题描述】

小蓝办了一个画展, 在一个画廊左右两边陈列了他自己的作品。为了使画展更有意思, 小蓝没有等距陈列自己的作品, 而是按照更有艺术感的方式陈列。在画廊的左边陈列了 $L$ 幅作品, 在画廊的右边陈列了 $R$ 幅作品, 左边的作品距离画廊的起点依次为 $u_1,u_2,\cdots ,u_L$, 右边的作品距离画廊起点依次为 $v_1,v_2,\cdots$, $v_R\circ$

每周, 小蓝要整理一遍自己的每一幅作品。整理一幅作品的时间是固定的,但是要带着沉重的工具。从一幅作品到另一幅作品之间的距离为直线段的长度。

小蓝从画廊的起点的正中央（左右两边的中点）出发, 整理好每一幅画,最终到达画廊的终点的正中央。已知画廊的宽为 $w_{\text{。 }}$

请问小蓝最少带着工具走多长的距离?

【输入格式】

输入的第一行包含四个整数 $L,R,d,w$, 表示画廊左边和右边的作品数量,以及画廊的长度和宽度。

第二行包含 $L$ 个正整数 $u_1,u_2,\cdots ,u_L$, 表示画廊左边的作品的位置。

第三行包含 $R$ 个正整数 $v_1,v_2,\cdots ,v_R$, 表示画廊右边的作品的位置。

【输出格式】

输出一个实数, 四舍五入保留两位小数, 表示小蓝最少带着工具走的距离。

【样例输入】

$\begin{array}{llll}3& 3& 10& 2\end{array}$

$\begin{array}{lll}1& 3& 8\end{array}$

$\begin{array}{lll}2& 4& 6\end{array}$

【样例输出】

$\begin{array}{l}14.71\end{array}$

【样例说明】

小蓝从起点开始, 首先到达左边第一幅作品 (走动距离 $\sqrt{2}$ ), 然后到达左边第二幅作品 (走动距离 2), 然后到达右边第一幅作品 (走动距离 $\sqrt{5}$ ), 然后到达右边第二幅和第三幅作品 (走动距离 2 和 2), 然后到达左边第三幅作品 (走动距离 $2\sqrt{2}$ ), 最后到达画廊终点 (走动距离 $\sqrt{5}$ )。

总共距离为 $\sqrt{2}+2+\sqrt{5}+2+2+2\sqrt{2}+\sqrt{5}\approx 14.71$ 。

【评测用例规模与约定】

对于 $40\%$ 的评测用例, $1\le L,R\le 10,1\le d\le 100,1\le w\le 100$ 。

对于 $70\%$ 的评测用例， $1\le L,R\le 100,1\le d\le 1000,1\le w\le 1000$ 。

对于所有评测用例, $1\le L,R\le 500,1\le d\le 100000,1\le w\le 100000$, $0\le u_1<u_2<\cdots <u_L\le d,0\le v_1<v_2<\cdots <v_R\le d。$

---

试题 J 答疑

时间限制: $3.0\mathrm{s}$ 内存限制: $512.0\mathrm{MB}$ 本题总分: 25 分

【问题描述】

有 $n$ 位同学同时找老师答疑。每位同学都颛先估计了自己答疑的时间。老师可以安排答疑的顺序, 同学们要依次进入老师办公室答疑。

一位同学答疑的过程如下:

1. 首先进入办公室, 编号为 $i$ 的同学需要 $s_i$ 毫秒的时间。
2. 然后同学问问题老师解答, 编号为 $i$ 的同学需要 $a_i$ 毫秒的时间。
3. 答疑完成后, 同学很高兴, 会在课程群里面发一条消息, 需要的时间可以忽略。
4. 最后同学收拾东西离开办公室, 需要 $e_i$ 毫秒的时间。一般需要 10 秒、 20 秒或 30 秒，即 $e_i$ 取值为 10000,20000 或 30000 。

一位同学离开办公室后, 紧接着下一位同学就可以进入办公室了。

答疑从 0 时刻开始。老师想合理的安排答疑的顺序, 使得同学们在课程群里面发消息的时刻之和最小。

【输入格式】

输入第一行包含一个整数 $n$, 表示同学的数量。

接下来 $n$ 行, 描述每位同学的时间。其中第 $i$ 行包含三个整数 $s_i,a_i,e_i$, 意义如上所述。

【输出格式】

输出一个整数, 表示同学们在课程群里面发消息的时刻之和最小是多少。

【样例输入】

$\begin{array}{l}3\end{array}$

$\begin{array}{lll}10000& 10000& 10000\end{array}$

$\begin{array}{lll}20000& 50000& 20000\end{array}$

$\begin{array}{lll}30000& 20000& 30000\end{array}$

【样例输出】

$\begin{array}{l}280000\end{array}$

【样例说明】

按照 $1,3,2$ 的顺序答疑，发消息的时间分别是 $20000,80000,180000$ 。

【评测用例规模与约定】

对于 $30\%$ 的评测用例， $1\le n\le 20$ 。

对于 $60\%$ 的评测用例, $1\le n\le 200$ 。

对于所有评测用例, $1\le n\le 1000,1\le s_i\le 60000,1\le a_i\le 1000000$, e i ∈ { 10000 , 20000 , 30000 } e_{i} \in\{10000,20000,30000\} ei​∈{10000,20000,30000}, 即 $e_i$ 一定是 $10000、20000、30000$ 之一。