探索大脑的微观世界:方向性连接如何丰富神经网络的功能复杂度
在神经科学领域,理解大脑如何通过其复杂的网络结构实现高级功能一直是一个核心议题。最近,一项由Nobuaki Monma和Hideaki Yamamoto博士领导的研究为我们提供了新的视角,他们通过创新的结合生物神经元培养皿实验和计算仿真模型,揭示了在生物神经网络中引入方向性连接如何显著影响网络的动态行为和功能性复杂度。
这次介绍主要针对数据分析和建模预测的部分进行介绍,湿实验的硬件部分有非常非常多的细节我们不打算深究,我们主要介绍湿实验的结论。
我们主要分成3块进行讲解,每块又分为4个小问题进行回答。
1.湿实验部分
- 湿实验部分,作者准备了哪些硬件?
- 采集得到的数据,做了哪些预处理?
- 为了分析实验数据,制定了哪些统计指标?
- 实验中的指标表现如何,得到了什么结论?
2.脉冲神经网络(SNN)仿真验证
- 什么是SNN脉冲神经元模型?
- SNN的常见模型?
- SNN仿真实验得到什么结论?
- SNN的适用场景?
3.状态转换模型 state-transition model仿真验证
- 什么是状态转移模型?
- 如何用状态转移模型进行稳态分析?
- 状态转移模型如何用于真实实验?
- 状态转移矩阵适用场景?
1.湿实验部分
本节介绍了 Monma & Yamamoto 2024 中基于状态转移模型来进行体外神经元培养皿分析的过程。目录如下:
- 湿实验部分,作者准备了哪些硬件?
- 采集得到的数据,做了哪些预处理?
- 为了分析实验数据,制定了哪些统计指标?
- 实验中的指标表现如何,得到了什么结论?
硬件准备
- 微流控设备制备:研究者使用聚二甲基硅氧烷(PDMS)通过复制模塑法制备了微流控设备。这些设备设计有非对称的微通道,用于引导神经元的轴突生长,从而实现网络中的方向性连接。
- 细胞培养:在PDMS微流控设备上,使用大鼠皮层神经元进行体外培养。神经元在微流控设备中的特定区域内生长和扩展,形成模块化的网络结构。
- 神经元生长和连接:通过时间序列成像技术,研究者观察了神经元在微流控设备中的轴突生长和连接。非对称微通道的设计使得轴突在特定方向(正向)的生长概率高于相反方向(反向)。
- 钙成像:为了记录神经元网络的自发活动,研究者使用了荧光钙探针GCaMP6s。通过共聚焦显微镜获取的钙成像数据,可以推断出神经元的电活动。
数据预处理
-
成像数据获取:首先,使用共聚焦显微镜和荧光钙探针(如GCaMP6s)记录神经元网络的钙信号。这些信号反映了神经元的电活动。
-
区域兴趣(ROI)定义:从钙成像记录中,研究者选择大约64个神经元(每个模块四个神经元),并在每个神经元周围绘制一个感兴趣区域(ROI)。ROI是用来量化特定神经元活动的工具。
-
荧光值提取:对于每个ROI,通过平均ROI内所有像素的荧光值来获取时间序列的荧光信号F(t)。
-
基线校正:为了去除成像过程中的漂白效应和背景噪声,计算相对荧光变化,
F ( t ) − F 0 ( t ) F 0 ( t ) \frac{F(t)-F_0(t)}{F0(t)} F0(t)F(t)−F0(t)
其中 F ( t ) F(t) F(t)是时间点t的荧光值, F 0 ( t ) F_0(t) F0(t)是ROI的基线荧光值。
-
活动率推断:使用CASCADE算法(一种基于卷积神经网络的方法)从相对荧光变化中推断出神经元的放电率xi(t)。CASCADE算法是通过对钙成像和膜片钳实验数据进行训练得到的。
-
信号传播分析:通过Schmitt触发器算法检测神经元的激活起始时间,并创建一个二进制时间序列Si(t)来表示神经元的激活状态。
统计指标有哪些
统计指标:全局网络激活 global network activation (GNA)
全局网络激活(GNA),符号表示为 Φ Φ Φ,被定义为参与集体活动事件的神经元的平均比例。如每次集体活动,参与神经元比例为100%,那么认为这个系统完全同步。
在获取了钙成像数据之后,研究人员进行了以下步骤来评估群体活动事件:
-
激活起始点的检测:首先,使用Schmitt触发器算法适应于神经元i的放电率xi(t),以检测神经元的激活起始点。
-
二进制时间序列的创建:基于检测到的起始点,创建了一个二进制时间序列Si(t),其中1表示检测到起始点。这里设置了上阈值(2 Hz)和下阈值(1 Hz),意味着当神经元的放电频率在这两个阈值之间时,认为是激活状态。比如一个二进制时间序列如下
0 1 0 0 0 0 0 0 1 0 0 0 1
-
集体活动事件的检测:通过对所有神经元的放电率xi(t)求和得到的群体放电率,使用Schmitt触发器方法来检测集体活动事件。这里同样设置了上阈值(10 Hz)和下阈值(5 Hz),用以识别涉及多个神经元的同步活动。比如对二进制时间序列求和如下
3 7 0 0 0 0 1 4 8 0 2 5 9
除了基于群体活动可以计算GNA。这些数据也可以量化信号的传播概率和传播延迟
统计指标:交叉相关函数 Cross-correlation function
交叉相关函数用来评估,两个神经元之间的延迟相关性。
神经元
i
i
i和
j
j
j的交叉相关函数定义为:
R i j ( τ ) = 1 T − τ ∑ l = 0 ( T − τ ) / Δ t − 1 S i ( l Δ t ) S j ( l Δ t − τ ) , R_{ij}(\tau)=\frac{1}{T-\tau} \sum_{l=0}^{(T-\tau) / \Delta t-1} S_i(l \Delta t) S_j(l \Delta t-\tau), Rij(τ)=T−τ1l=0∑(T−τ)/Δt−1Si(lΔt)Sj(lΔt−τ),
- T T T 是记录的持续时间( = 1200 =1200 =1200秒), Δ t \Delta t Δt是时间步长( = 0.01 =0.01 =0.01秒)
- S i ( t ) S_i(t) Si(t)表示第 i i i个神经元在时刻 t t t的状态
- τ \tau τ是时间延迟( − 1.0 < τ < 1.0 -1.0<\tau<1.0 −1.0<τ<1.0秒)
- 指标 i i i和 j j j分配给上游和下游模块中的神经元,以设置反向和正向传播之间的负和正延迟
- 通过首先将交叉相关函数标准化为 R ^ i j ( τ ) = R i j ( τ ) R i i ( 0 ) R j j ( 0 ) \hat{R}_{ij}(\tau)=\frac{R_{ij}(\tau)}{\sqrt{R_{ii}(0) R_{jj}(0)}} R^ij(τ)=Rii(0)Rjj(0)Rij(τ)
- 对所有具有跳数 h h h 的 i − j i-j i−j 对求平均值,其中 h h h被定义为从神经元 i i i到神经元 j j j在正向方向上所需的非对称微通道的最小数量,从而获得累积交叉相关函数 ⟨ R ^ i j ( τ ) ⟩ h \langle\hat{R}_{ij}(\tau)\rangle_h ⟨R^ij(τ)⟩h
h 被设置得越大,相当于对i-j对筛选条件就越严格,因为对于 i 所在模块到 j 所在模块的连接就越多。相当于筛选出更紧密的神经元对进行统计。
非对称微通道(Asymmetric Microchannels): 微流控设备设计的非常微小的非对称几何形状的通道。
例如,如果节点B总是在节点A发放之后的5个时间间隔之后发放,则
R A B ( 5 ) = 1 R_{AB}(5)=1 RAB(5)=1
统计指标:平均相关系数
先给出神经元 i 和 j 的相关系数计算公式,就是普通皮尔逊相关系数
r i j = ∑ t [ x i ( t ) − x ˉ i ] ⋅ [ x j ( t ) − x ˉ j ] ∑ t [ x i ( t ) − x ˉ i ] 2 ∑ t [ x j ( t ) − x ˉ j ] 2 r_{i j}=\frac{\sum_t\left[x_i(t)-\bar{x}_i\right] \cdot\left[x_j(t)-\bar{x}_j\right]}{\sqrt{\sum_t\left[x_i(t)-\bar{x}_i\right]^2} \sqrt{\sum_t\left[x_j(t)-\bar{x}_j\right]^2}} rij=∑t[xi(t)−xˉi]2∑t[xj(t)−xˉj]2∑t[xi(t)−xˉi]⋅[xj(t)−xˉj]
由于作者只希望度量不同模块之间相关系数(不考虑相同模块时的相关系数),所以
⟨ r i j ⟩ = 1 M ∑ i ≠ j r i j ( 1 − δ ( m i , m j ) ) \lang r_{ij}\rang = \frac{1}{M}\sum_{i \neq j} r_{i j}\left(1-\delta\left(m_i, m_j\right)\right) ⟨rij⟩=M1i=j∑rij(1−δ(mi,mj))
其中:
- Kronecker delta function δ i j = { 1 if i = j 0 if i ≠ j \delta_{i j}= \begin{cases}1 & \text { if } i=j \\ 0 & \text { if } i \neq j\end{cases} δij={10 if i=j if i=j,
- m i m_i mi表示第 i i i 个节点的模块索引。从而当模块相同时, 1 − δ ( m i , m j ) 1-\delta(m_i, m_j) 1−δ(mi,mj)为0
- M = ∑ i ≠ j ( 1 − δ ( m i , m j ) ) M=\sum_{i \neq j}\left(1-\delta\left(m_i, m_j\right)\right) M=∑i=j(1−δ(mi,mj)) 是归一化常数
统计指标 - 功能复杂性指标
因为不同状态最终以概率分布的形式存在,故相关系数在不同范围也有不同的概率。
将相关系数概率分布从 0 到 1 切分成
B
=
20
B=20
B=20 份,第 k 份的相关系数的概率大小用
p
k
(
r
i
j
)
p_k(r_{ij})
pk(rij) 表示。注意这里k表示份数,而不是状态索引
Θ = 1 − B 2 ( B − 1 ) ∑ k = 1 B ∣ p k ( r i j ) − 1 B ∣ \Theta=1-\frac{B}{2(B-1)} \sum_{k=1}^B\left|p_k\left(r_{i j}\right)-\frac{1}{B}\right| Θ=1−2(B−1)Bk=1∑B pk(rij)−B1
其实我感觉公式应该是
Θ = 1 − B ( B − 1 ) ∑ k = 1 B ∣ p k ( r i j ) − 1 B ∣ \Theta=1-\frac{B}{(B-1)} \sum_{k=1}^B\left|p_k\left(r_{i j}\right)-\frac{1}{B}\right| Θ=1−(B−1)Bk=1∑B pk(rij)−B1
比如
-
当相关系数平均分布于每一个小格子中时,此时意味系统在某个时刻的状态,完全平均的处于任何一种状态。
此时每个格子中的概率都是 1 / B 1/B 1/B,此时 Θ = 1 \Theta=1 Θ=1 -
当系统的复杂性没那么强,对于某一个特定的相关系数有很大的概率,比如某个相关系数的概率为1。此时有
Θ = 1 − B ( B − 1 ) ⋅ ( B − 1 B ) = 0 \Theta=1-\frac{B}{(B-1)} \cdot\left(\frac{B-1}{B}\right)=0 Θ=1−(B−1)B⋅(BB−1)=0
实验结果
时间序列对比
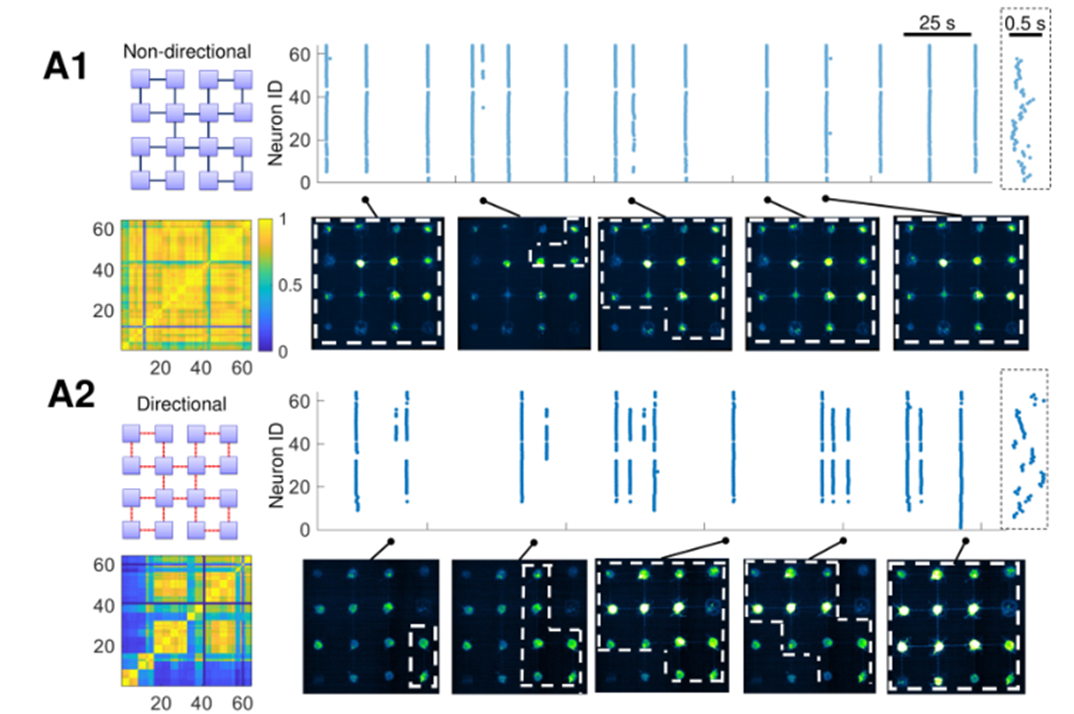
- A1展示了 没有方向诱导 的培养皿。从右图来看同步性较强。左下还展示了他们的相关性矩阵,没有方向诱导的相关性矩阵,明显强于方向诱导的相关性矩阵。
- A2展示了 方向诱导 的培养皿,从右图中可以看出它们同步性较弱,而且体现了更丰富的动力学行为(发放的模式有长有短,有同步也有异步)
统计指标-GNA, 平均相关系数,功能复杂度
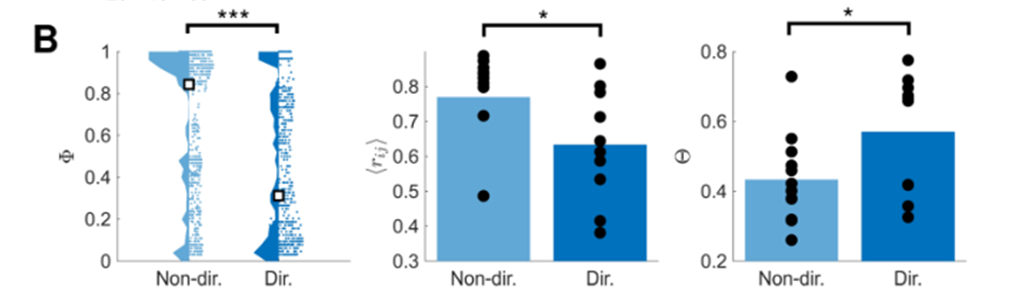
- 左图:展示了 Φ ( GNA ) \Phi (\text{GNA}) Φ(GNA) 在 无方向 和 有方向 的培养皿中的差异。小方块标识了它们的中位数。可以看到,增加了方向性之后,全局网络激活 指标变小了。这意味着方向性的增加会导致同步性的减弱。
- 中图:平均相关系数。增加方向性之后,平均相关系数变小了。
- 右图:功能复杂度。增加方向性之后,网络的功能复杂度增加了。
统计指标-累计交叉相关系数
R i j ( τ ) = 1 T − τ ∑ l = 0 ( T − τ ) / Δ t − 1 S i ( l Δ t ) S j ( l Δ t − τ ) , R_{ij}(\tau)=\frac{1}{T-\tau} \sum_{l=0}^{(T-\tau) / \Delta t-1} S_i(l \Delta t) S_j(l \Delta t-\tau), Rij(τ)=T−τ1l=0∑(T−τ)/Δt−1Si(lΔt)Sj(lΔt−τ),
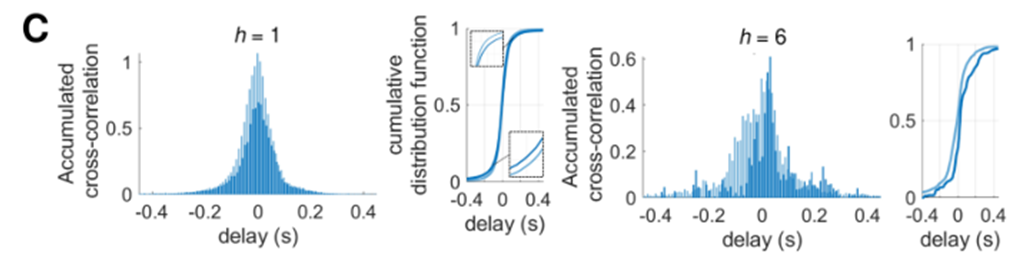
- 其中深蓝色表示有方向,浅蓝色表示无方向。
- h=1 表示只要从 节点i所在的模块 到 节点j所在的模块 有1条连边,则纳入统计的范围。可以看出此时相关性下降,但时间延迟差不多
- h=6 相当于查看了紧密连接的神经元的传播延迟,可以看出时间延迟出现了明显的下降。且 τ \tau τ 的分布明显右偏,表明此时,i 节点闪烁之后 j 节点闪烁的传播延迟更加明显。
小结
在湿实验部分中,研究者主要完成了以下内容
-
微流控设备的设计与应用:
- 研究者利用微流控技术构建了具有层次化模块化结构的神经元网络。
- 通过微流控设备中的非对称微通道实现了神经元网络中的方向性连接,模拟了生物神经系统中的轴突导向。
-
神经元网络的动态监测与分析:
- 使用荧光钙成像技术记录了神经元网络的自发活动,并通过成像数据监测了网络动态。
- 通过定义感兴趣区域(ROI)和计算相对荧光变化,研究者量化了神经元的放电率和网络的同步性。
-
网络结构与功能的关系:
- 研究者发现,引入方向性连接可以减少网络的过度同步,并增加整合-分离平衡,从而提高功能性复杂度。
- 通过比较具有不同方向性连接的网络,研究者揭示了网络拓扑结构对神经网络动态特性的影响。
即将发布:揭秘尖峰神经网络(SNN)仿真验证 —— 探索大脑模拟的新前沿
在神经科学和人工智能的交汇点上,尖峰神经网络(SNN)正逐渐成为研究大脑功能和开发新一代计算模型的有力工具。我们的下一篇博客文章将深入探讨SNN的奥秘,从基本的脉冲神经元模型到复杂的网络仿真实验,我们将揭示SNN如何帮助我们更好地理解大脑的工作方式。
以下是您将在本文中发现的主题:
-
SNN脉冲神经元模型的基础知识:我们将介绍SNN中的脉冲神经元模型,这是模拟生物神经元放电行为的基石。
-
SNN的常见模型:从简单的积分-发放模型到复杂的动态阈值模型,我们将概述当前研究中使用的SNN模型。
-
SNN仿真实验的洞见:通过仿真实验,研究者能够得到哪些关于神经网络动态和信息处理的结论?
-
SNN的适用场景:SNN在哪些领域展现出其独特的优势,它们又是如何推动人工智能和神经科学研究的?
相关链接
- 动力学重构/微分方程参数拟合 - 基于模型
- 论文泛读 - 基于RNN建模: Reconstructing computational system dynamics from neural data with recurrent neural
- 如何从数据中计算Lyapunov指数|Alan Wolf|Matlab源码
- 非线性动力学/混沌系统/复杂性科学/系统科学常用工具打包