栈队列经典OJ题（详细过程）

news2024/12/29 9:18:25

1. 有效的括号 - 力扣（LeetCode）

  第一题判断有效的括号，这道题我们会用到栈的知识，栈是后进先出的，可以根据这个来解这道题，先看一下题目和示例。

1.1整体思路 

我们通过示例可以看出括号匹配就返回true，不匹配就返回false，这里的思路就是使用栈，如果是左括号，我们就入栈，如果是右括号，我们就取栈顶元素和右括号进行比较，如果匹配就比较下一个，不匹配直接返回false，我们可以结合图例来理解一下！

 以上是一些常见的例子，但是也有一些特殊的情况

1.']'只有一个右括号时，这个时候我们就需要加一些条件，如果栈顶没有元素，证明没有左括号入栈，那么也就是说没有左括号和右括号匹配，那就直接返回false。

2.'['只有一个括号时，那么也就是说只有左括号入栈，然后就直接返回了，这里我们可以用判断一下栈是否为空，用bool来返回，如果为空，返回true，如果不是空，证明栈里还有左括号，那也说明左括号和右扩号的数量不匹配，这样就可以有效解决了

1.2代码分析 

因为还没有学C++，所以这里的栈都是自己模拟实现的

1.3整体代码

typedef char STDatatype;

typedef struct Stack
{
	STDatatype* a;
	int top;
	int capacity;
}ST;


//函数声明
//函数的初始化和销毁
void STInit(ST* pst);
void STDestroy(ST* pst);

//进栈和出栈
void STPush(ST* pst, STDatatype x);
void STPop(ST* pst);

//栈顶
STDatatype STTop(ST* pst);

//栈是否为空
bool STEmpty(ST* pst);

//个数
int STSize(ST* pst);
//函数的初始化和销毁
void STInit(ST* pst)
{
	assert(pst);
	pst->a = NULL;
	pst->top = pst->capacity = 0;
}
void STDestroy(ST* pst)
{
	assert(pst);
	free(pst->a);
	pst->a = NULL;
	pst->top = pst->capacity = 0;
}
//进栈和出栈
void STPush(ST* pst, STDatatype x)
{
	assert(pst);
	if (pst->capacity == pst->top)
	{
		//增加容量
		int newcapacity = pst->capacity == 0 ? 4 : 2 * pst->capacity;
		STDatatype* tmp = (STDatatype*)realloc(pst->a,sizeof(STDatatype)*newcapacity);
		if (tmp == NULL)
		{
			perror("realloc");
			exit(1);
		}
		pst->a = tmp;
		pst->capacity = newcapacity;
	}
	pst->a[pst->top] = x;
	pst->top++;
}
void STPop(ST* pst)
{
	assert(pst);
	assert(pst->top > 0);
	pst->top--;
}
//栈顶
STDatatype STTop(ST* pst)
{
	assert(pst);
	assert(pst->top > 0);
	return pst->a[pst->top - 1];
}
//栈是否为空
bool STEmpty(ST* pst)
{
	assert(pst);
	return pst->top == 0;
	//等于就是空，不等于0就是非空
}
//个数
int STSize(ST* pst)
{
	assert(pst);
	return pst->top;
}
bool isValid(char* s) {
    ST st;
   STInit(&st);
   while(*s != 0)
   {
    //左括号入栈
    if(*s == '(' || *s == '[' || *s == '{')
    {
        STPush(&st,*s);
    }
    else
    {
         if(STEmpty(&st))
         {
             return false;
         }
        char top = STTop(&st);
        STPop(&st);
        if(top == '(' && *s != ')'
        || top == '{' && *s != '}'
        || top == '[' && *s != ']')
        {
            return false;
        }
        
    }
    ++s;
   }
  bool ret = STEmpty(&st);
  return ret;
}

 2. 用队列实现栈

这道题是让我们用两个队列来实现一个栈，我们知道队列是先进先出的，而栈是后进先出的，那我们要如何实现呢？

2.1整体思路：

这道题的思路就是我们把要插入的数据放到那个非空的队列中，要保持一个队列是空，一个队列是非空，注意不可以两个队列都有数据，这样我们会把自己绕进去！要删除数据的时候，将非空队列的最后一个数据留下来，将其他的插入到空的队列当中，然后再将留下的那个数据删除即可。画图来理解一下

 

2.2 代码分析

2.3整体代码 

//创建节点

typedef int QDatatype;
typedef struct Queuenode
{
	QDatatype val;
	struct Queuenode* next;
}Qnode;

//定义一个结构体存放指针
typedef struct Queue
{
	Qnode* phead;
	Qnode* ptail;
	int size;
}Queue;

//队列的初始化和销毁
void QueueInit(Queue* pq);
void QueueDestory(Queue* pq);

//队列的插入和删除
void QueuePush(Queue* pq, QDatatype x);
void QueuePop(Queue* pq);

//取队列头和尾的值
QDatatype QueueFront(Queue* pq);
QDatatype QueueBank(Queue* pq);

//是否为空
bool QueueEmpty(Queue* pq);

//size
int QueueSize(Queue* pq);

//队列的初始化和销毁
void QueueInit(Queue* pq)
{
	assert(pq);
	pq->phead = NULL;
	pq->ptail = NULL;
	pq->size = 0;
}
void QueueDestory(Queue* pq)
{
	assert(pq);
	Qnode* cur = pq->phead;
	while (cur)
	{
		Qnode* next = cur->next;
		free(cur);
		cur = next;
	}
	pq->phead = pq->ptail = NULL;
	pq->size = 0;
}

//队列的插入和删除
void QueuePush(Queue* pq, QDatatype x)
{
	assert(pq);
	Qnode* newnode = (Qnode*)malloc(sizeof(Qnode));
	if (newnode == NULL)
	{
		perror("malloc:");
		exit(1);
	}
	//申请成功
	newnode->next = NULL;
	newnode->val = x;
	if (pq->ptail == NULL)
	{
		pq->phead = pq->ptail = newnode;
	}
	else
	{
		pq->ptail->next = newnode;
		pq->ptail = newnode;
	}
	pq->size++;
}

void QueuePop(Queue* pq)
{
	assert(pq);
	assert(pq->size != 0);
	//一个节点
	if (pq->phead == pq->ptail)
	{
		free(pq->phead);
		pq->phead = pq->ptail = NULL;
	}
	else
	{
		//多个节点
		Qnode* next = pq->phead->next;
		free(pq->phead);
		pq->phead = next;
	}
	pq->size--;
}

//取队列头和尾的值
QDatatype QueueFront(Queue* pq)
{
	assert(pq);
	assert(pq->phead);
	return pq->phead->val;
}
QDatatype QueueBank(Queue* pq)
{
	assert(pq);
	assert(pq->ptail);
	return pq->ptail->val;
}

//是否为空
bool QueueEmpty(Queue* pq)
{
	assert(pq);
	return pq->size == 0;
}

//size
int QueueSize(Queue* pq)
{
	assert(pq);
	return pq->size;
}

//匿名结构体
typedef struct {
   Queue q1;
   Queue q2; 
} MyStack;


MyStack* myStackCreate() {
    MyStack* obj =(MyStack*)malloc(sizeof(MyStack));
    QueueInit(&(obj->q1));
    QueueInit(&(obj->q2));
    return obj; 
}

void myStackPush(MyStack* obj, int x) {
    if(!QueueEmpty(&(obj->q1)))
    {
        QueuePush(&(obj->q1),x);
    }
    else
    {
        QueuePush(&(obj->q2),x);
    }
}

int myStackPop(MyStack* obj) {
    Queue* empty = &(obj->q1);
    Queue* noempty = &(obj->q2);
    if(!QueueEmpty(&(obj->q1)))
    {
        empty = &(obj->q2);
        noempty = &(obj->q1);
    }
    while(QueueSize(noempty) > 1)
    {
        QueuePush(empty,QueueFront(noempty));
        QueuePop(noempty);
    }
    int top = QueueFront(noempty);
    QueuePop(noempty);
    return top;
}

int myStackTop(MyStack* obj) {
    if(!QueueEmpty(&(obj->q1)))
    {
        return QueueBank(&(obj->q1));
    }
    else
    {
        return QueueBank(&(obj->q2));
    }
}

bool myStackEmpty(MyStack* obj) {
    return QueueEmpty(&(obj->q1)) && QueueEmpty(&(obj->q2));
}

void myStackFree(MyStack* obj) {
    QueueDestory(&(obj->q1));
    QueueDestory(&(obj->q2));
    free(obj);
}

/**
 * Your MyStack struct will be instantiated and called as such:
 * MyStack* obj = myStackCreate();
 * myStackPush(obj, x);
 
 * int param_2 = myStackPop(obj);
 
 * int param_3 = myStackTop(obj);
 
 * bool param_4 = myStackEmpty(obj);
 
 * myStackFree(obj);
*/

 3. 用栈实现队列

这道题是用两个栈实现队列，栈是后进先出，队列是先进先出，这个就比较好实现了

3.1整体思路

我们可以建一个pushst和一个popst，一个用来插入数据，一个用来删除数据，我们可以想一下将数据插入到pushst，栈是后进先出，那么我们将pushst的数据倒到popst，他们的顺序就发生了改变，这个时候popst栈顶的数据也就是队列第一个要出的数据，我们可以画图来看一下。这里还有一个小技巧，当popst不为空的时候，取栈顶就是队列要出的数据，这里不用来回倒，插入数据直接插入pustst即可，当popst为空时把pushst的数据都倒入到popst栈中

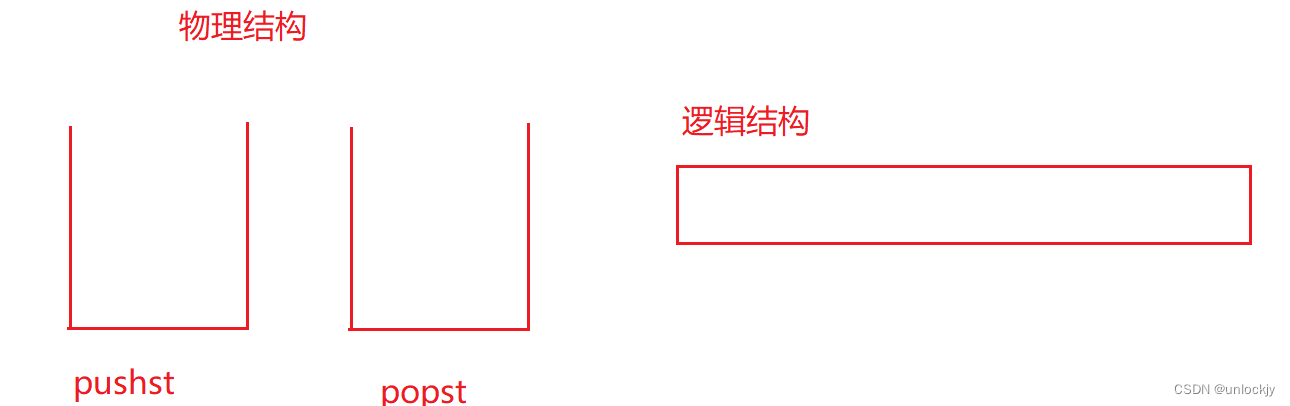
3.2代码分析 

3.3整体代码 



typedef int STDatatype;

typedef struct Stack
{
	STDatatype* a;
	int top;
	int capacity;
}ST;

//函数声明
//函数的初始化和销毁
void STInit(ST* pst);
void STDestroy(ST* pst);

//进栈和出栈
void STPush(ST* pst, STDatatype x);
void STPop(ST* pst);

//栈顶
STDatatype STTop(ST* pst);

//栈是否为空
bool STEmpty(ST* pst);

//个数
int STSize(ST* pst);


//函数的初始化和销毁
void STInit(ST* pst)
{
	assert(pst);
	pst->a = NULL;
	pst->top = pst->capacity = 0;
}


void STDestroy(ST* pst)
{
	assert(pst);
	free(pst->a);
	pst->a = NULL;
	pst->top = pst->capacity = 0;
}

//进栈和出栈
void STPush(ST* pst, STDatatype x)
{
	assert(pst);
	if (pst->capacity == pst->top)
	{
		//增加容量
		int newcapacity = pst->capacity == 0 ? 4 : 2 * pst->capacity;
		STDatatype* tmp = (STDatatype*)realloc(pst->a,sizeof(STDatatype)*newcapacity);
		if (tmp == NULL)
		{
			perror("realloc");
			exit(1);
		}
		pst->a = tmp;
		pst->capacity = newcapacity;
	}
	pst->a[pst->top] = x;
	pst->top++;
}
void STPop(ST* pst)
{
	assert(pst);
	assert(pst->top > 0);
	pst->top--;
}

//栈顶
STDatatype STTop(ST* pst)
{
	assert(pst);
	assert(pst->top > 0);
	return pst->a[pst->top - 1];
}

//栈是否为空
bool STEmpty(ST* pst)
{
	assert(pst);
	return pst->top == 0;
	//等于就是空，不等于0就是非空
}

//个数
int STSize(ST* pst)
{
	assert(pst);
	return pst->top;
}

typedef struct {
   ST pushst;
   ST popst; 
} MyQueue;


MyQueue* myQueueCreate() {
    MyQueue* obj = (MyQueue*)malloc(sizeof(MyQueue));
    STInit(&obj->pushst);
    STInit(&obj->popst);
    return obj;
}

void myQueuePush(MyQueue* obj, int x) {
    STPush(&obj->pushst,x);
}


int myQueuePeek(MyQueue* obj) {
    if(STEmpty(&obj->popst))
    {
        while(!STEmpty(&obj->pushst))
        {
            STPush(&obj->popst,STTop(&obj->pushst));
            STPop(&obj->pushst);
        }
    }
    return STTop(&obj->popst);
}

int myQueuePop(MyQueue* obj) {
    int f = myQueuePeek(obj);
    STPop(&obj->popst);
    return f;
}

bool myQueueEmpty(MyQueue* obj) {
    return STEmpty(&obj->pushst) && STEmpty(&obj->popst);
}

void myQueueFree(MyQueue* obj) {
    STDestroy(&obj->popst);
    STDestroy(&obj->pushst);
    free(obj);
}

/**
 * Your MyQueue struct will be instantiated and called as such:
 * MyQueue* obj = myQueueCreate();
 * myQueuePush(obj, x);
 
 * int param_2 = myQueuePop(obj);
 
 * int param_3 = myQueuePeek(obj);
 
 * bool param_4 = myQueueEmpty(obj);
 
 * myQueueFree(obj);
*/

4.​​​​​​​设计循环队列

这道题是让我们设计一个循环队列，队列是先进先出的，是一个循环，可以把他比较一个图书馆的桌子，有四个座位，也就是说最多可以坐四个人，如果超过四个人后面的人就要等待在坐的四个人有人坐，再坐进去，拿这个例子我们就可以很好的理解这个题目了！

4.1整体思路

这道题有多种解法，可以用链表来做，也可以用数组来做，在这里我还是用数组来做，链表比较麻烦，不论是在申请空间，还是找尾节点的前驱节点，大家感兴趣可以拿链表做一下，这里就拿数组做了，拿数组做也有出现一些小问题，如果我们只申请k个空间，那么数组是空还是满我们就分不清了，这里可以画图来看一下!

这里有两种解法，一个是定义一个计数器，还有一个是多开一个空间，就是开k+1个空间，这样我们就可以分清是空还是非空了，还有一个点就是如何让他循环起来，就是使用%，也就是每次到尾%回到下标为0的元素，这里我就采用多开一个空间的方法了，也就是%（k+1）这里画图可以帮助大家理解一下 。

这里将把每一个函数都拿出来分析！

4.2代码分析

4.2.1MyCircularQueue(k)

4.2.2isEmpty()

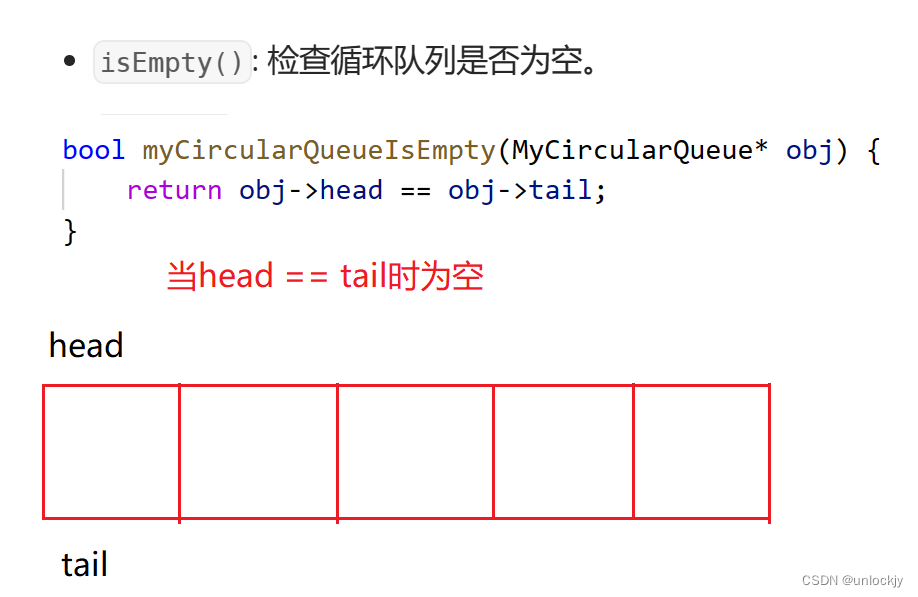
4.2.3isfull 

 4.2.4enQueue(value)和deQueue()

4.2.5Front和Rear

4.3整体代码




typedef struct {
    int* a;
    int head;
    int tail;
    int k;
} MyCircularQueue;


MyCircularQueue* myCircularQueueCreate(int k) {
    MyCircularQueue* obj = (MyCircularQueue*)malloc(sizeof(MyCircularQueue));
    obj->a = (int*)malloc(sizeof(int)*(k+1));
    obj->head = 0;
    obj->tail = 0;
    obj->k = k;
    return obj;  
}


bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
    return obj->head == obj->tail;
}

bool myCircularQueueIsFull(MyCircularQueue* obj) {
    return  (obj->tail+1) % (obj->k+1) == obj->head;
}

bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
    if(myCircularQueueIsFull(obj))
    {
        return false;
    }
    obj->a[obj->tail] = value;
    obj->tail++;
    obj->tail %= (obj->k+1);
    return true;
}

bool myCircularQueueDeQueue(MyCircularQueue* obj) {
    if(myCircularQueueIsEmpty(obj))
    {
        return false;
    }
    obj->head++;
    obj->head %= (obj->k+1);
    return true;
}

int myCircularQueueFront(MyCircularQueue* obj) {
    if(myCircularQueueIsEmpty(obj))
    {
        return -1;
    }
    else
    return obj->a[obj->head];
}

int myCircularQueueRear(MyCircularQueue* obj) {
    if(myCircularQueueIsEmpty(obj))
    {
        return -1;
    }
    else
   return obj->a[(obj->tail -1 + obj->k +1) % (obj->k+1)];
   //return obj->tail == 0 ? obj->a[obj->k]:obj->a[obj->tail-1];
}



void myCircularQueueFree(MyCircularQueue* obj) {
    free(obj->a);
    free(obj);
}

/**
 * Your MyCircularQueue struct will be instantiated and called as such:
 * MyCircularQueue* obj = myCircularQueueCreate(k);
 * bool param_1 = myCircularQueueEnQueue(obj, value);
 
 * bool param_2 = myCircularQueueDeQueue(obj);
 
 * int param_3 = myCircularQueueFront(obj);
 
 * int param_4 = myCircularQueueRear(obj);
 
 * bool param_5 = myCircularQueueIsEmpty(obj);
 
 * bool param_6 = myCircularQueueIsFull(obj);
 
 * myCircularQueueFree(obj);
*/

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1672896.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【STM32 |示例程序】EXTI中断示例程序（对射式红外传感器旋转编码器计次）

【STM32 |示例程序】EXTI中断示例程序（对射式红外传感器旋转编码器计次）

✨✨谢谢大家捧场，祝屏幕前的小伙伴们每天都有好运相伴左右，一定要天天开心哦！✨✨ 🎈🎈作者主页： 丠丠64-CSDN博客🎈🎈 ✨✨ 帅哥美女们，我们共同加油！一起…
阅读更多...
MinIO学习笔记

MinIO学习笔记

MINIO干什么用的： AI数据基础设施的对象存储 为人工智能系统提供数据支持，数据存储；对象存储（Object Storage）是一种数据存储架构，它以对象为单位来处理、存储和检索数据，每个对象都包含了数据本…
阅读更多...
Maven、JavaWeb基础开发

Maven、JavaWeb基础开发

1 Maven介绍 1、标准化的项目结构 2、标准化的构建流程 3、依赖管理 4、依赖范围 2 JavaWeb基础开发 2.1 Http协议 1 Http请求数据格式 2 Http响应数据格式 2.2 Web服务器（Tomcat） VTS、FileServer使用Tomcat部署； 其他服务单元TESLA S…
阅读更多...
前端使用Compressor.js实现图片压缩上传

前端使用Compressor.js实现图片压缩上传

前端使用Compressor.js实现图片压缩上传 Compressor.js官方文档 安装 npm install compressorjs使用 在使用ElementUI或者其他UI框架的上传组件时，都会有上传之前的钩子函数，在这个函数中可以拿到原始file，这里我用VantUI的上传做演示 a…
阅读更多...
.NET开源、功能强大、跨平台的图表库LiveChart2

.NET开源、功能强大、跨平台的图表库LiveChart2

LiveCharts2 是 从LiveCharts演变而来，它修复了其前身的主要设计问题，它专注于在任何地方运行，提高了灵活性，并继承LiveCharts原有功能。 极其灵活的数据展示图库 （效果图） 开始使用 Live charts 是 .Net 的跨平台图表库，请访问 https://livecharts.dev 并查看目标平…
阅读更多...
大模型管理工具：SWIFT

大模型管理工具：SWIFT

目录 一、SWIFT 介绍 二、SWIFT 安装 2.0 配置环境(可选) 2.1 使用pip进行安装 2.2 源代码安装 2.3 启动 WEB-UI 三、部署模型 3.0 deploy命令参数 3.1 原始模型 3.2 微调后模型 一、SWIFT 介绍 SWIFT（Scalable lightWeight Infrastructure for Fine-Tuni…
阅读更多...
一、VIsual Studio下的Qt环境配置（Visual Studio 2022 + Qt 5.12.10）

一、VIsual Studio下的Qt环境配置（Visual Studio 2022 + Qt 5.12.10）

一、下载编译器Visual Studio2022和Qt 5.12.10 Visual Studio 2022 社区版就够学习使用了 Qt5.12.10 安装教程网上搜，一大堆 也很简单，配置直接选默认，路径留意一下即可 二、配置环境 Ⅰ，配置Qt环境变量 系统变量下的Path&a…
阅读更多...
tomcat 的启动流程

tomcat 的启动流程

tomcat 的启动流程 中 使用的Lifecycle 生命流程 。在这里还使用了设计模式中的模板模式（LifecycleBase 是一个模板类） init（）方法 start() 方法 container 的处理
阅读更多...
CNN/TCN/LSTM/BiGRU-Attention到底哪个模型效果最好？注意力机制全家桶来啦！

CNN/TCN/LSTM/BiGRU-Attention到底哪个模型效果最好？注意力机制全家桶来啦！

​ 声明：文章是从本人公众号中复制而来，因此，想最新最快了解各类智能优化算法及其改进的朋友，可关注我的公众号：强盛机器学习，不定期会有很多免费代码分享~ 目录 数据介绍 效果展示 原理简介 代…
阅读更多...
MySQL8.0就地升级到MySQL8.4.0

MySQL8.0就地升级到MySQL8.4.0

MySQL8.0就地升级到MySQL8.4.0 升级需求：将8.0.35升级到8.4.0,以In-Place方式直接升级到MySQL8.4.0。 数据库版本 操作系统版本 原版本 8.0.35 Centos7.9 x86_64 新版本 8.4.0 Centos7.9 x86_64 关闭现有版本MySQL，将二进制或包替换成新版本并…
阅读更多...
小红薯视频作品一键克隆，解放双手自动搬运【永久脚本+使用教程】

小红薯视频作品一键克隆，解放双手自动搬运【永久脚本+使用教程】

软件介绍： 小红薯作品搬运神器，软件只需要复制对方的作品链接即可一键克隆搬运到自己的小红书上，再也不用手动去复制粘贴了，批量起号搬运必备神器 设备需求： 电脑 链接：https://pan.baidu.com/s/11MzBqER…
阅读更多...
Automa：一键自动化，网页数据采集与工作流程优化专家

Automa：一键自动化，网页数据采集与工作流程优化专家

Automa：解锁自动化浏览器潜能，赋能工作效率，让复杂任务变得简单- 精选真开源，释放新价值。 概览 Automa是一款创新的网页自动化工具，专为寻求提升工作效率、简化数据收集过程的现代工作者设计。它融合了先进的数据抓取…
阅读更多...
SpringAI集成本地AI大模型ollama（调用篇）非常简单！！

SpringAI集成本地AI大模型ollama（调用篇）非常简单！！

一，前提准备本地ai模型 1，首先需要去ollama官网下载开源ai到本地 网址：Ollama 直接下载到本地，然后启动ollama 启动完成后，我们可以在cmd中执行ollama可以看到相关命令行 2， 下载ai moudle 然后我们需要…
阅读更多...
【MQTT】paho.mqtt.c 库的“介绍、下载、交叉编译” 详解，以及编写MQTT客户端例子源码

【MQTT】paho.mqtt.c 库的“介绍、下载、交叉编译” 详解，以及编写MQTT客户端例子源码

😁博客主页😁：🚀https://blog.csdn.net/wkd_007🚀 🤑博客内容🤑：🍭嵌入式开发、Linux、C语言、C、数据结构、音视频🍭 ⏰发布时间⏰：2024-05-13 1…
阅读更多...
《系统架构设计师教程（第2版）》第11章-未来信息综合技术-01-信息物理系统（CPS）技术概述

《系统架构设计师教程（第2版）》第11章-未来信息综合技术-01-信息物理系统（CPS）技术概述

文章目录 1. 信息物理系统（CPS）1.1 来源1.2 定义1.3 本质 2. CPS的实现2.1 CPS 的体系架构2.1.1 单元级2.1.2 系统级2.1.3 SoS级 2.2 CPS 的技术体系2.2.1 感知和自动控制1）智能感知技术2）虚实融合控制技术 2.2.2 工业软件2.2.3 工…
阅读更多...
常用的内外网文件传输方式及优缺点

常用的内外网文件传输方式及优缺点

在现代企业环境中，内外网文件传输是一项至关重要的任务。这涉及到数据的安全性、传输效率以及操作的便捷性等多个方面。 每种方式都有其独特的优缺点，下面我们将逐一进行分析。 1、FileLink 优势：FileLink是一款专用于企业内外网隔离后的文…
阅读更多...
Cocos Creator 3.8.x 透明带滚动功能的容器

Cocos Creator 3.8.x 透明带滚动功能的容器

ScrollView 是一种带滚动功能的容器 1、删除ScrollView下Sprite组件的SpriteFrame 2、ScrollView下scrollBar的Sprite组件的Color设为：FFFFFF00 3、ScrollView下view的Graphics组件的FillColor设为：FFFFFF00
阅读更多...
python下载及安装

python下载及安装

1、python下载地址： Python Releases for Windows | Python.orgThe official home of the Python Programming Languagehttps://www.python.org/downloads/windows/ 2、python安装 （1） 直接点击下载后的可执行文件.exe （2&…
阅读更多...
高频电源模块TL22010-T2整流模块TL22010-T3用途

高频电源模块TL22010-T2整流模块TL22010-T3用途

直流屏充电模块TL22010-T2电源模块TL22010-T3，整流模块TL11010-T3，其他TL系列型号有：TL11020-T3，TL11010-T2，TL11020-T2，TL22010-T，TL-22010-T，TL-11010-T，TL-22005-T&am…
阅读更多...
Django5.0入门基本使用

Django5.0入门基本使用

文章目录 一、安装1、安装django环境2、创建项目3、启动服务器4、创建第一个应用（1）创建应用（2）编写视图（3）映射url（4）测试 二、核心概念1、django.urls 函数（1&#xff…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023