---

1.找出所有子集的异或总和再求和

1.题目链接

• 找出所有子集的异或总和再求和

---

2.算法原理详解

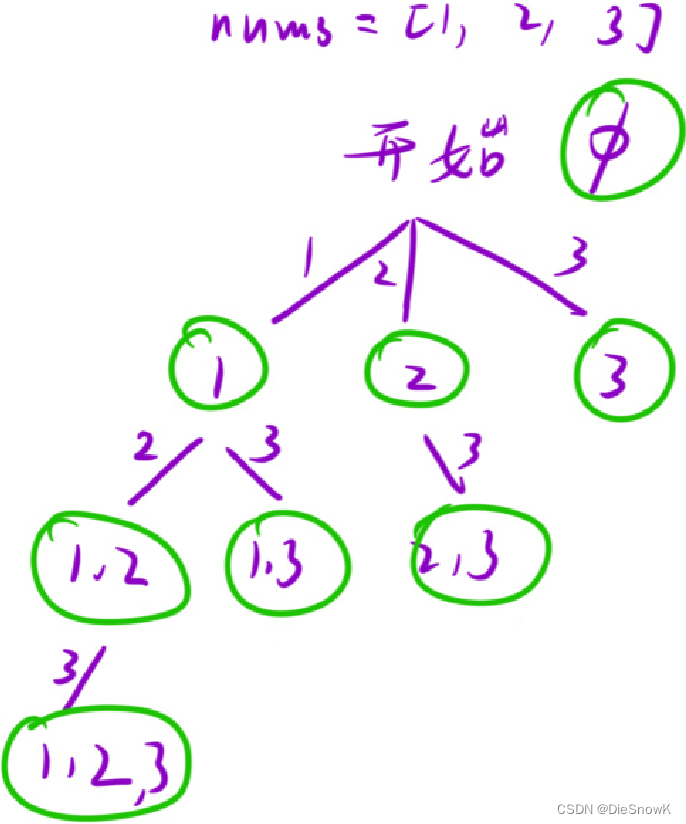
• 思路：每次都只选一个数，此后只能选它后面的数
  • 全局变量：
    • int path
    • int sum
  • DFS()设计
    • 函数头：void DFS(nums, pos)
      • pos：下一层递归选择数时的起始下标
    • 函数体：
      • 循环枚举还能选哪些数
    • 递归出口：不需要特定函数出口
  • 回溯：亦或运算消消乐
    

---

3.代码实现

class Solution 
{
    int sum = 0;
    int path = 0;
public:
    int subsetXORSum(vector<int>& nums) 
    {
        DFS(nums, 0);
        return sum;
    }
    
    void DFS(vector<int>& nums, int pos)
    {
        sum += path;
        
        for(int i = pos; i < nums.size(); i++)
        {
            path ^= nums[i];
            DFS(nums, i + 1);
            path ^= nums[i]; // 回溯，恢复现场
        }
    }
};

---

2.全排列 II

1.题目链接

• 全排列 II

---

2.算法原理详解

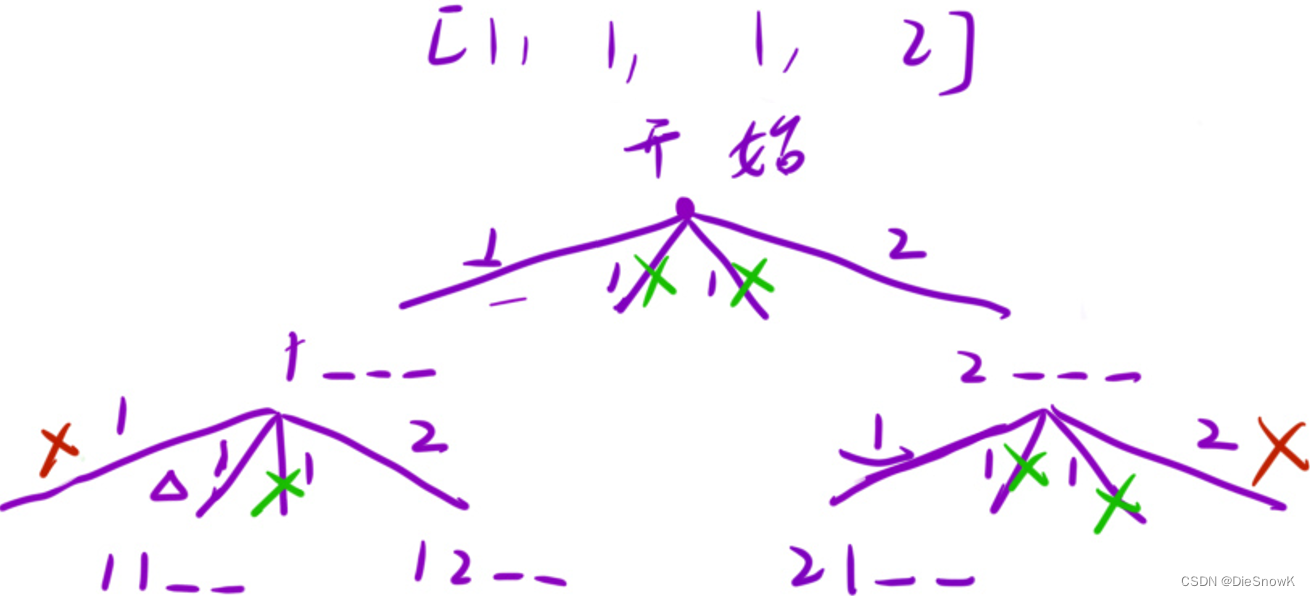
• 本题与全排列的区别就是本题主要考察剪枝
• 剪枝情况：
  • 同一个节点的所有分支中，相同的元素只能选择一次
    • nums[i] == nums[i - 1]，则剪枝
  • 同一个数只能使用一次
    • 使用check数组剪枝
• 剪枝思路：前提 -> 先把整个数组排序
  • 思路一：只关心”不合法”的分支
    • check[i] == true || (i != 0 && nums[i] == nums[i - 1] && check[i - 1] = false)
  • 思路二：只关心”合法”的分支
    • check[i] == false && (i == 0 || nums[i] != nums[i - 1] || check[i - 1] == true)
    • nums[i] != nums[i - 1]不成立隐含了一个条件nums[i] == nums[i - 1]，此时才去看条件check[i - 1] == true
      

---

3.代码实现

// 剪枝 v1.0
class Solution 
{
    vector<vector<int>> ret;
    vector<int> path;
    vector<bool> check;
public:
    vector<vector<int>> permuteUnique(vector<int>& nums) 
    {
        check.resize(nums.size(), false);
        sort(nums.begin(), nums.end());
        
        DFS(nums);
        return ret;
    }
    
    void DFS(vector<int>& nums)
    {
        if(path.size() == nums.size())
        {
            ret.push_back(path);
            return;
        }
        
        for(int i = 0; i < nums.size(); i++)
        {
            // 剪纸 - 何时不进？
            if(check[i] == true || \
              (i != 0 && nums[i]== nums[i - 1] && check[i - 1] == false))
            {
                continue;
            }
            
            // 进
            path.push_back(nums[i]);
            check[i] = true;
            
            DFS(nums);
            
            path.pop_back(); // 回溯，恢复现场
            check[i] = false;
            
        }
    }
};
--------------------------------------------------------------------------------
// 剪枝 v2.0
class Solution 
{
    vector<vector<int>> ret;
    vector<int> path;
    vector<bool> check;
public:
    vector<vector<int>> permuteUnique(vector<int>& nums) 
    {
        check.resize(nums.size(), false);
        sort(nums.begin(), nums.end());
        
        DFS(nums);
        return ret;
    }
    
    void DFS(vector<int>& nums)
    {
        if(path.size() == nums.size())
        {
            ret.push_back(path);
            return;
        }
        
        for(int i = 0; i < nums.size(); i++)
        {
            // 剪纸 - 何时进？
            if(check[i] == false && \
              (i == 0 || nums[i] != nums[i - 1] || check[i - 1] == true))
            {
                path.push_back(nums[i]);
                check[i] = true;
                
                DFS(nums);
                
                path.pop_back(); // 回溯，恢复现场
                check[i] = false;
            }
        }
    }
};

---

3.电话号码的字母组合

1.题目链接

• 电话号码的字母组合

---

2.算法原理详解

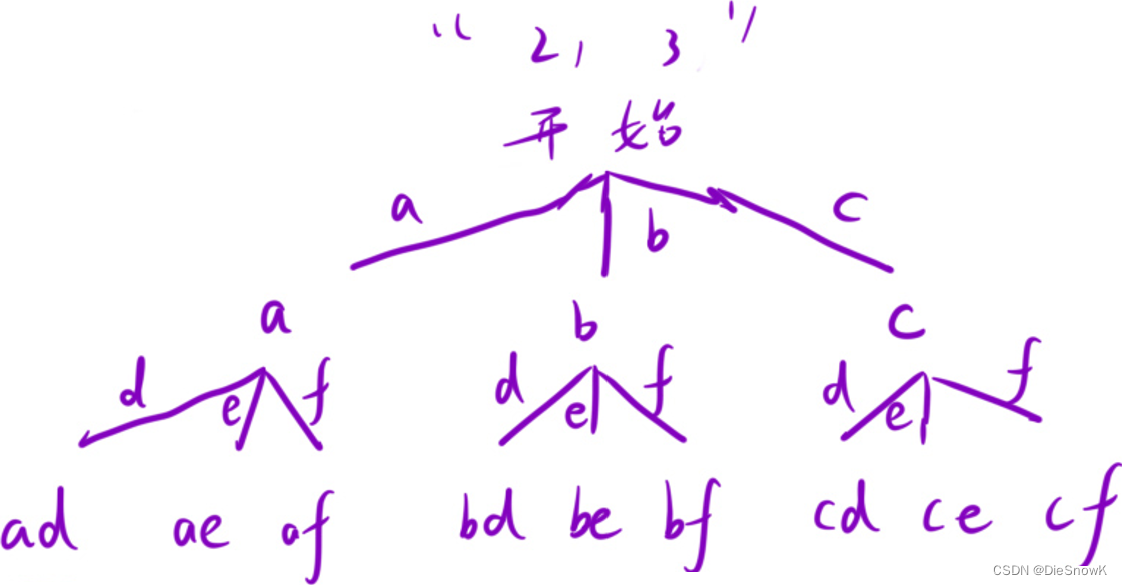
• 本题为组合问题，大思路几乎与排列问题一致
• 函数设计思路：
  • 全局变量：
    • string path
    • vector<string> ret
    • string [10]
  • DFS()设计：DFS(digits, pos)
  • 递归出口：path.size() == digits.size()
• 细节：数字与字符串的映射关系 -> 字符串数组
  

---

3.代码实现

class Solution 
{
    vector<string> ret;
    string path;
    
    // 按键映射字母
    string str[10] = {"", "", "abc", "def", \
        "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
public:
    vector<string> letterCombinations(string digits) 
    {
        if(digits.size() == 0)
        {
            return ret;
        }
        
        DFS(digits, 0);
        return ret;
    }
    
    void DFS(string& digits, int pos)
    {
        if(path.size() == digits.size())
        {
            ret.push_back(path);
            return;
        }
        
        for(auto& ch : str[digits[pos] - '0'])
        {
            path += ch;
            DFS(digits, pos + 1);
            path.pop_back(); // 回溯，恢复现场
        }
    }
};

---

4.括号生成

1.题目链接

• 括号生成

---

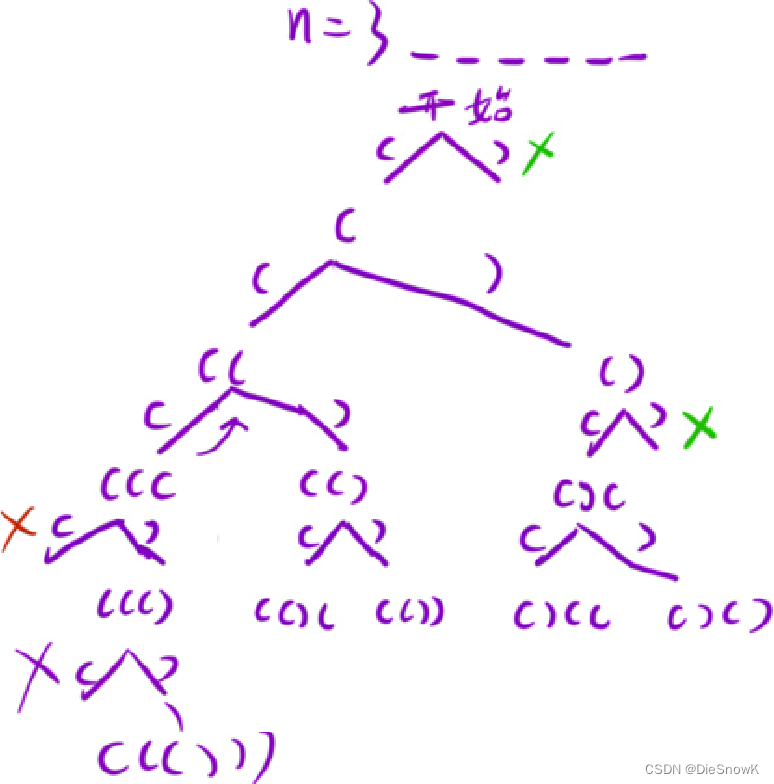
2.算法原理详解

• 首先要搞清楚，什么是有效的括号组合？
  1. 左括号的数量 = 右括号的数量
  2. 从头开始的任意一个子串，左括号的数量 >= 右括号的数量
• 函数设计思路：
  • 全局变量：
    • int left, right, total
    • string path
    • vector<string> path
  • DFS()设计：void DFS()
  • 递归出口：right == n
  • 回溯：左括号递归返回后
  • 剪枝：
    • left >= n
    • right >= left
      

---

3.代码实现

class Solution 
{
    int left;
    int right = 0;
    int total = 0;

    string path;
    vector<string> ret;
public:
    vector<string> generateParenthesis(int n) 
    {
        total = n;
        DFS();
        return ret;
    }

    void DFS()
    {
        if(right == total)
        {
            ret.push_back(path);
        }

        // 递归 + 剪枝
        if(left < total)
        {
            path += '(';
            left++;

            DFS();
            
            // 回溯，恢复现场
            path.pop_back();
            left--;
        }

        if(right < left)
        {
            path += ')';
            right++;

            DFS();

            // 回溯，恢复现场
            path.pop_back(); 
            right--;
        }
    }
};