【2293. 极大极小游戏】

news2024/11/26 20:42:08

来源：力扣（LeetCode）

描述：

给你一个下标从 0 开始的整数数组 nums ，其长度是 2 的幂。

对 nums 执行下述算法：

设 n 等于 nums 的长度，如果 n == 1 ，终止算法过程。否则，创建一个新的整数数组 newNums ，新数组长度为 n / 2 ，下标从 0 开始。
对于满足 0 <= i < n / 2 的每个偶数下标 i ，将 newNums[i] 赋值为 min(nums[2 * i], nums[2 * i + 1]) 。
对于满足 0 <= i < n / 2 的每个奇数下标 i ，将 newNums[i] 赋值为 max(nums[2 * i], nums[2 * i + 1]) 。
用 newNums 替换 nums 。
从步骤 1 开始重复整个过程。

执行算法后，返回 nums 中剩下的那个数字。

示例 1：

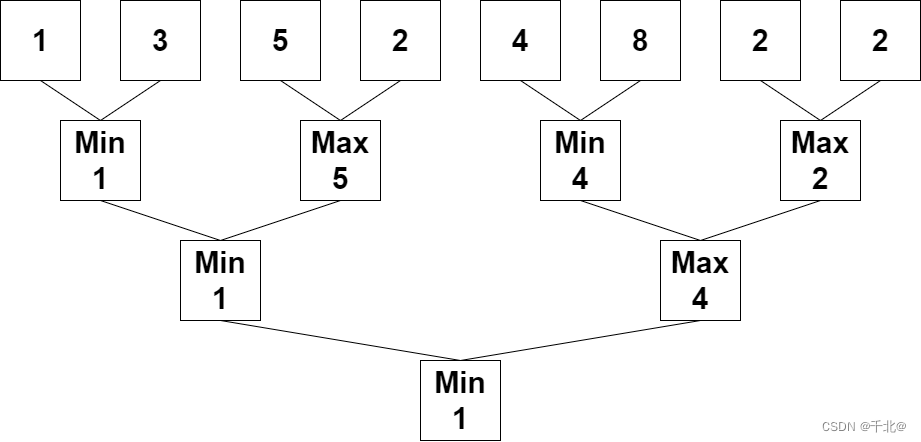
输入：nums = [1,3,5,2,4,8,2,2]
输出：1
解释：重复执行算法会得到下述数组。
第一轮：nums = [1,5,4,2]
第二轮：nums = [1,4]
第三轮：nums = [1]
1 是最后剩下的那个数字，返回 1 。

示例 2：

输入：nums = [3]
输出：3
解释：3 就是最后剩下的数字，返回 3 。

提示：

1 <= nums.length <= 1024
1 <= nums[i] <= 10⁹
nums.length 是 2 的幂

方法一：递归

思路与算法

若数组 nums 的长度 n 等于 1，我们直接返回 nums[0] 作为答案。否则，按照题意求出一个长度为 n / 2 的数组 newNums，递归求解 newNums 的答案即可。

代码：

class Solution {
public:
    int minMaxGame(vector<int>& nums) {
        int n = nums.size();
        if (n == 1) {
            return nums[0];
        }
        vector<int> newNums(n / 2);
        for (int i = 0; i < newNums.size(); i++) {
            if (i % 2 == 0) {
                newNums[i] = min(nums[2 * i], nums[2 * i + 1]);
            } else {
                newNums[i] = max(nums[2 * i], nums[2 * i + 1]);
            }
        }
        return minMaxGame(newNums);
    }
};

执行用时：8 ms, 在所有 C++ 提交中击败了52.55%的用户
内存消耗：9.7 MB, 在所有 C++ 提交中击败了28.90%的用户
复杂度分析
时间复杂度：O(n)。
空间复杂度：O(n)。

方法二：模拟

思路与算法

我们用一个循环来模拟整个过程，循环的条件是 n != 1，其中 n 是 nums 的长度。循环内，我们按照题意求出 newNums，然后用 newNums 替换 nums 即可。最后返回 nums[0] 作为答案。

代码：

class Solution {
public:
    int minMaxGame(vector<int>& nums) {
        int n = nums.size();
        while (n != 1) {
            vector<int> newNums(n / 2);
            for (int i = 0; i < newNums.size(); i++) {
                if (i % 2 == 0) {
                    newNums[i] = min(nums[2 * i], nums[2 * i + 1]);
                } else {
                    newNums[i] = max(nums[2 * i], nums[2 * i + 1]);
                }
            }
            nums = newNums;
            n /= 2;
        }
        return nums[0];
    }
};

执行用时：0 ms, 在所有 C++ 提交中击败了100.00%的用户
内存消耗：9.8 MB, 在所有 C++ 提交中击败了18.39%的用户
复杂度分析
时间复杂度：O(n)，其中 n 是数组 nums 的长度。
空间复杂度：O(n)，其中 n 是数组 nums 的长度。

方法三：原地修改

思路与算法

注意到在顺序遍历的情况下， newNums[i] 的计算结果可以直接存储到 nums[i] 中。这是因为 nums[i] 早在计算 newNums[⌊i / 2⌋] 时就已经被使用，而且它在未来一定不会再被使用。有一个特例是 i = 0，但此时可以原地修改的原因是很显然的。

代码:

class Solution {
public:
    int minMaxGame(vector<int>& nums) {
        int n = nums.size();
        while (n != 1) {
            int m = n / 2;
            for (int i = 0; i < m; i++) {
                if (i % 2 == 0) {
                    nums[i] = min(nums[2 * i], nums[2 * i + 1]);
                } else {
                    nums[i] = max(nums[2 * i], nums[2 * i + 1]);
                }
            }
            n = m;
        }
        return nums[0];
    }
};