一、集成学习
集成学习:通过建立几个模型来解决单一预测问题,工作原理是生成多个分类器/模型,各自独立地学习和作出预测。这些预测最后结合成组合预测,因此优于任何一个单分类的做出预测
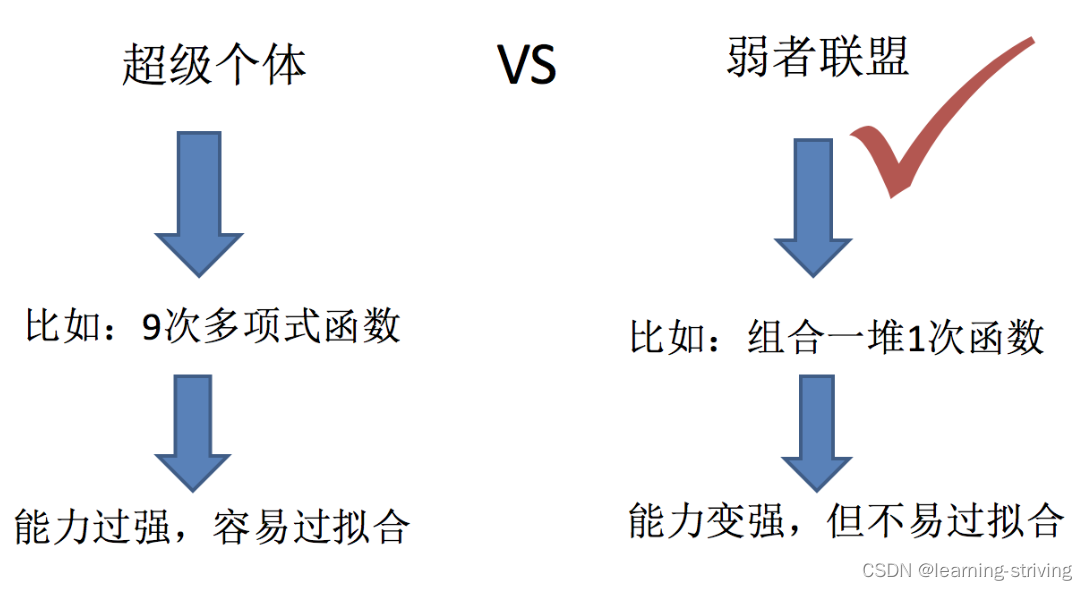
机器学习的两个核心任务

集成学习中boosting和Bagging

只要单分类器的表现不太差,集成学习的结果总是要好于单分类器的
二、Bagging集成原理
bagging集成优点:Bagging + 决策树/线性回归/逻辑回归/深度学习… = bagging集成学习方法,经过该方式组成的集成学习方法,均可在原有算法上提高约2%左右的泛化正确率,且简单、方便、 通用
目标:把下面的圈和方块进行分类

实现过程:
1.采样不同数据集

2.训练分类器

3.平权投票,获取最终结果
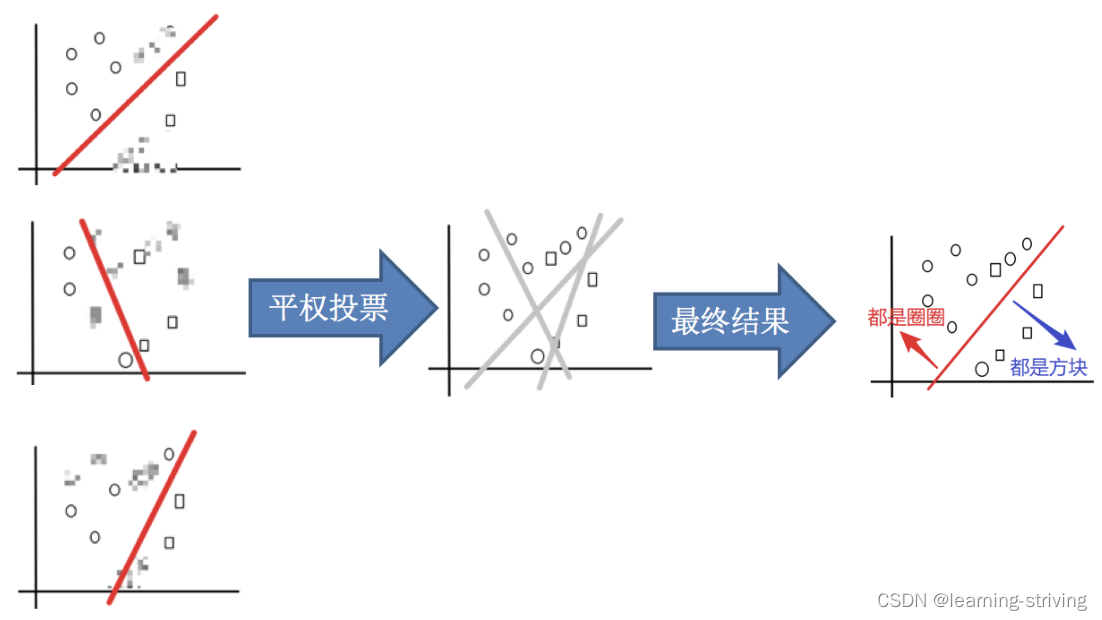
4.主要实现过程小结

三、随机森林构造过程
在机器学习中,随机森林是一个包含多个决策树的分类器,并且其输出的类别是由个别树输出的类别的众数而定,随机森林 = Bagging + 决策树
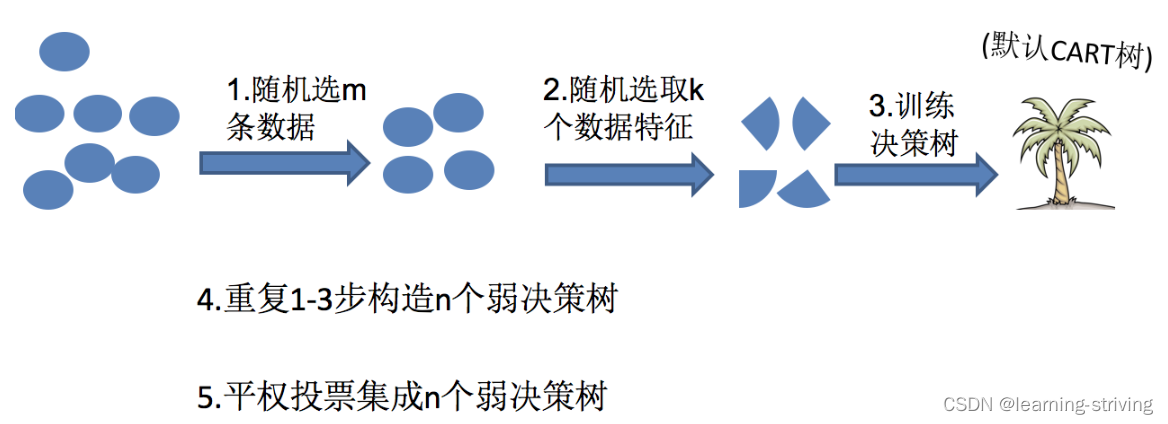
例如训练了5个树,其中有4个树的结果是True,1个树的结果是False,那么最终投票结果就是True
随机森林够造过程中的关键步骤(用N来表示训练用例(样本)的个数,M表示特征数目):
- 一次随机选出一个样本,有放回的抽样,重复N次(有可能出现重复的样本)
- 随机去选出m个特征,m<<M,建立决策树
- 随机抽样训练集原因:若不进行随机抽样,每棵树的训练集都一样,那么最终训练出的树分类结果也是完全一样的
- 有放回地抽样原因:若不是有放回的抽样,那么每棵树的训练样本都是不同的,都是没有交集的,这样每棵树都是“有偏的”,也就是说每棵树训练出来都是有很大的差异的;而随机森林最后分类取决于多棵树(弱分类器)的投票表决
四、随机森林api介绍
- sklearn.ensemble.RandomForestClassifier(n_estimators=10, criterion=’gini’, max_depth=None, bootstrap=True, random_state=None, min_samples_split=2)
- n_estimators:整型,可选,默认为10,森林里的树木数量120,200,300,500,800,1200
- Criterion:string,可选,默认为“gini”,分割特征的测量方法
- max_depth:整型或None,可选,默认None,树的最大深度 5,8,15,25,30
- max_features="auto”,每个决策树的最大特征数量
- If "auto", then
max_features=sqrt(n_features). - If "sqrt", then
max_features=sqrt(n_features)(same as "auto"). - If "log2", then
max_features=log2(n_features). - If None, then
max_features=n_features.
- If "auto", then
- bootstrap:boolean,可选,默认为True,是否在构建树时使用放回抽样
- min_samples_split:节点划分最少样本数
- min_samples_leaf:叶子节点的最小样本数
- 超参数:n_estimator, max_depth, min_samples_split,min_samples_leaf
五、随机森林预测案例
使用泰坦尼克号乘客生存数据操作过程如下


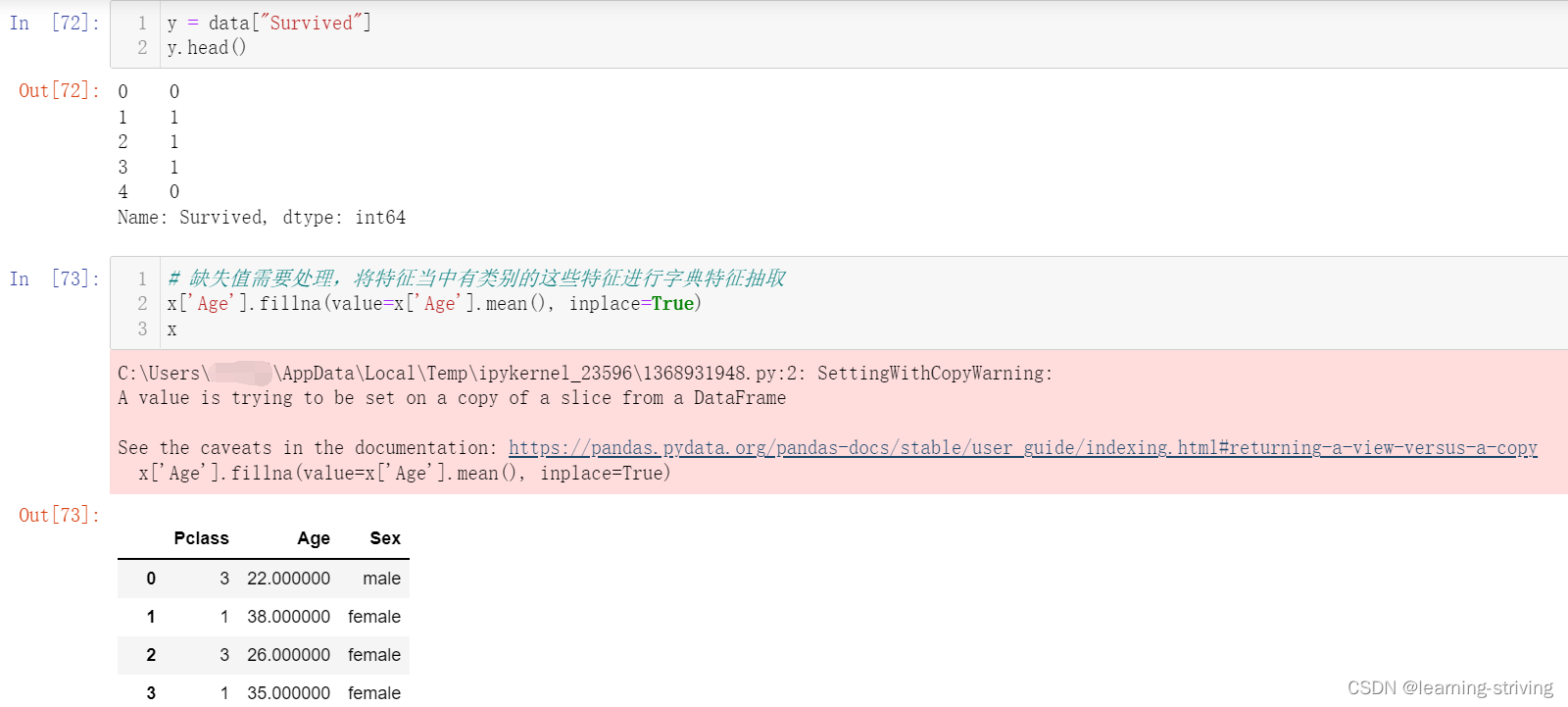
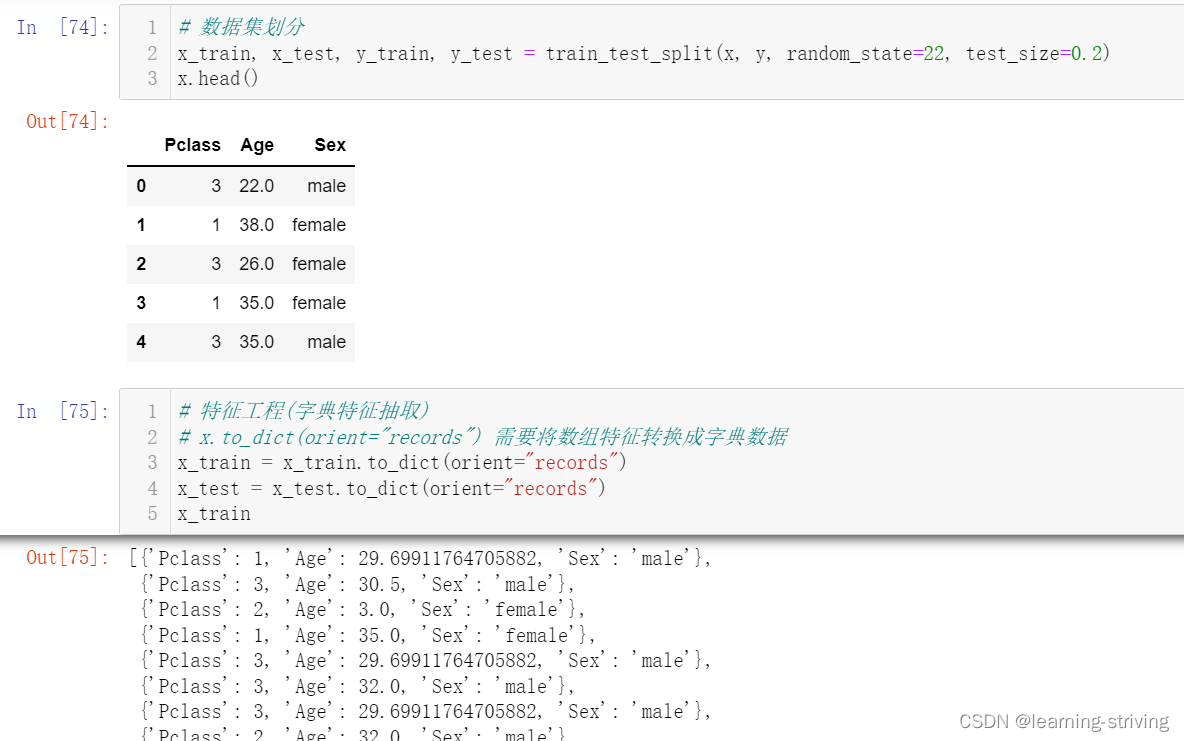

完整代码如下
import pandas as pd
import numpy as np
from sklearn.feature_extraction import DictVectorizer
from sklearn.model_selection import train_test_split,GridSearchCV
# from sklearn.tree import DecisionTreeClassifier, export_graphviz
from sklearn.ensemble import RandomForestClassifier
data = pd.read_csv('../data/train.csv')
data
------------------------------------------------------------------
data.describe()
# 数据基本处理,确定特征值、目标值
x = data[["Pclass", "Age", "Sex"]]
x
y = data["Survived"]
y.head()
# 缺失值需要处理,将特征当中有类别的这些特征进行字典特征抽取
x['Age'].fillna(value=x['Age'].mean(), inplace=True)
x
# 数据集划分
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=22, test_size=0.2)
x.head()
# 特征工程(字典特征抽取)
# x.to_dict(orient="records") 需要将数组特征转换成字典数据
x_train = x_train.to_dict(orient="records")
x_test = x_test.to_dict(orient="records")
x_train
# 特征中出现类别符号,需要进行one-hot编码处理(DictVectorizer)
transfer = DictVectorizer() # 实例化一个转换器类
x_train = transfer.fit_transform(x_train) # 调用fit_transform方法输入数据并转换,返回sparse矩阵
x_test = transfer.fit_transform(x_test)
x_train
-------------------------------------------------------
# 机器学习(随机森林),模型训练
estimator = RandomForestClassifier()
param_grid = {"n_estimators": [120,200,300,500,800,1200], "max_depth": [5, 8, 15, 25, 30]} # 定义超参数的选择列表
estimator = GridSearchCV(estimator,param_grid=param_grid,cv=5) # 使用GridSearchCV进行网格搜索,超参数调优
estimator.fit(x_train, y_train)
estimator.best_estimator_
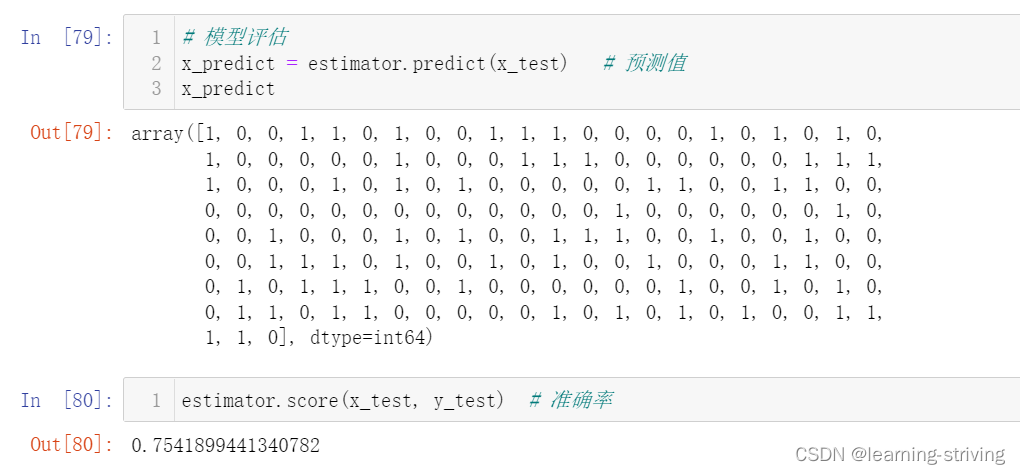
# 模型评估
x_predict = estimator.predict(x_test) # 预测值
x_predict
estimator.score(x_test, y_test) # 准确率六、boosting集成原理
boosting:随着学习的积累从弱到强,简而言之就是每新加入一个弱学习器,整体能力就会得到提升,代表算法有Adaboost,GBDT,XGBoost
实现过程如下
1.训练第一个学习器
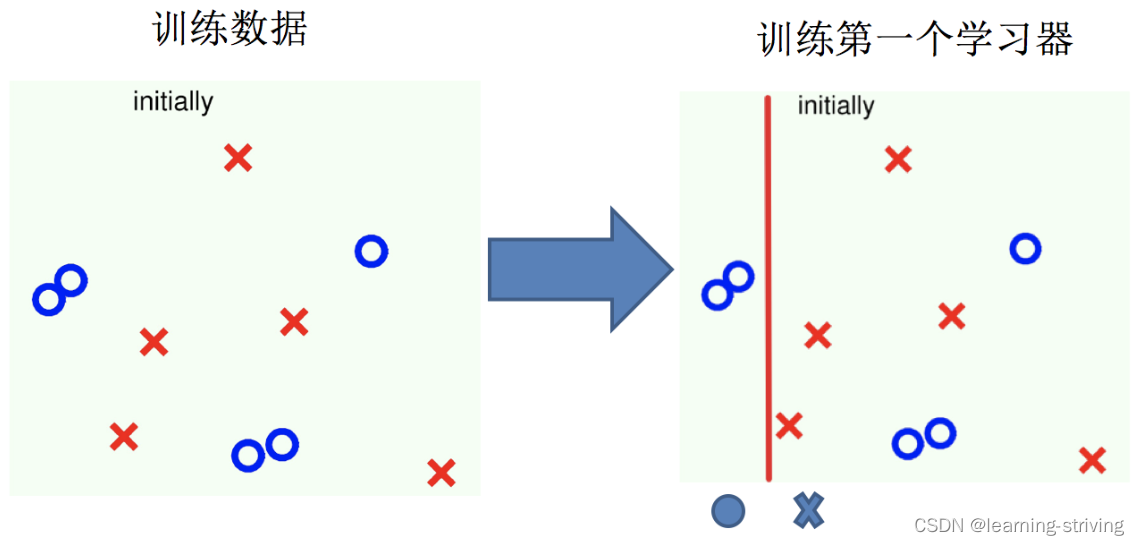
2.调整数据分布

3.训练第二个学习器

4.再次调整数据分布

5.依次训练学习器,调整数据分布

6.整体过程实现
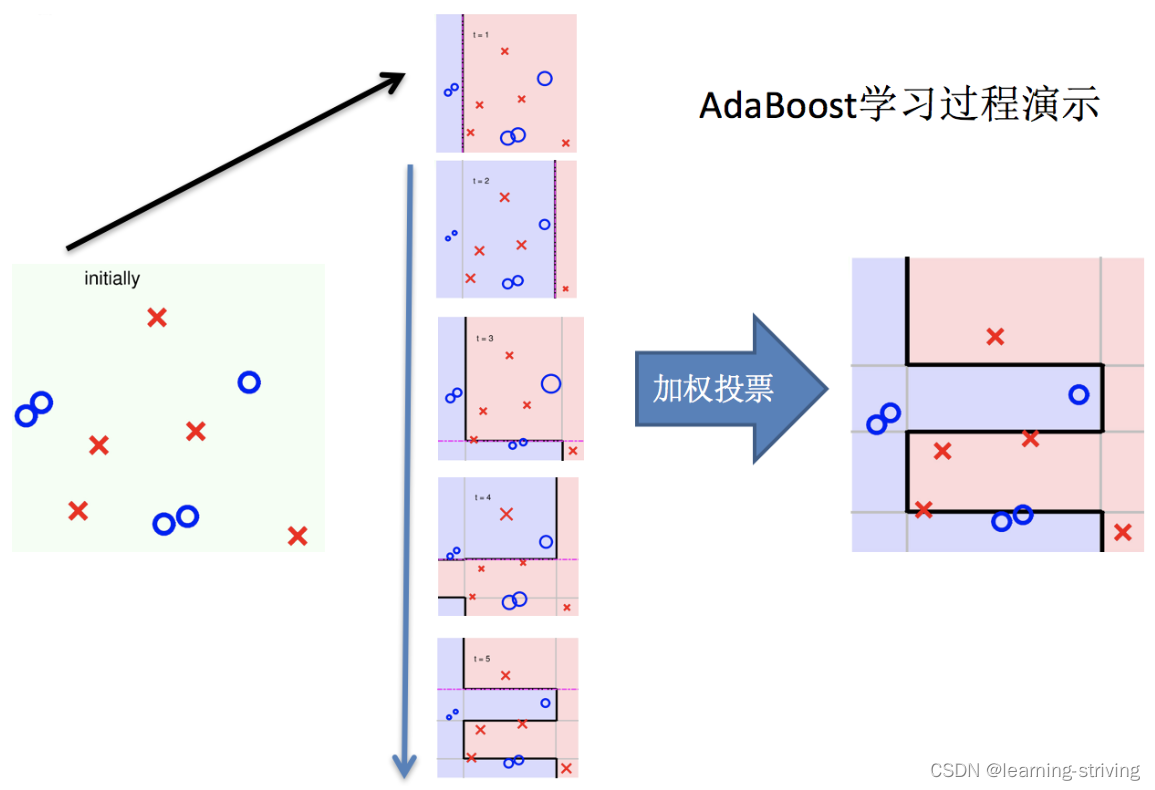
关键点

AdaBoost的构造过程小结

bagging集成与boosting集成的区别
| 区别 | Bagging | Boosting |
| 数据方面 | 对数据进行采样训练 | 根据前一轮学习结果调整数据的重要性 |
| 投票方面 | 所有学习器平权投票 | 对学习器进行加权投票 |
| 学习顺序 | 学习是并行的,每个学习器没有依赖关系 | 学习是串行,学习有先后顺序 |
| 主要作用 | 用于提高泛化性能(解决过拟合,也可以说降低方差) | 用于提高训练精度 (解决欠拟合,也可以说降低偏差) |

api介绍:from sklearn.ensemble import AdaBoostClassifier
- api链接:sklearn.ensemble.AdaBoostClassifier — scikit-learn 1.2.0 documentation
七、梯度提升决策树(GBDT)
梯度提升决策树(GBDT Gradient Boosting Decision Tree):是一种迭代的决策树算法,该算法由多棵决策树组成,所有树的结论累加起来做最终答案。它在被提出之初就被认为是泛化能力(generalization)较强的算法。近些年更因为被用于搜索排序的机器学习模型而引起大家关注。
GBDT = 梯度下降 + Boosting + 决策树
GBDT主要执行思想
- 使用梯度下降法优化代价函数
- 使用一层决策树作为弱学习器,负梯度作为目标值
- 利用boosting思想进行集成
八、XGBoost
XGBoost= 二阶泰勒展开+boosting+决策树+正则化
面试题:XGBoost的原理
回答要点:二阶泰勒展开,boosting,决策树,正则化
- Boosting:XGBoost使用Boosting提升思想对多个弱学习器进行迭代式学习
- 二阶泰勒展开:每一轮学习中,XGBoost对损失函数进行二阶泰勒展开,使用一阶和二阶梯度进行优化
- 决策树:在每一轮学习中,XGBoost使用决策树算法作为弱学习进行优化
- 正则化:在优化过程中XGBoost为防止过拟合,在损失函数中加入惩罚项,限制决策树的叶子节点个数以及决策树叶子节点的值
泰勒展开式:泰勒展开越多,计算结果越精确
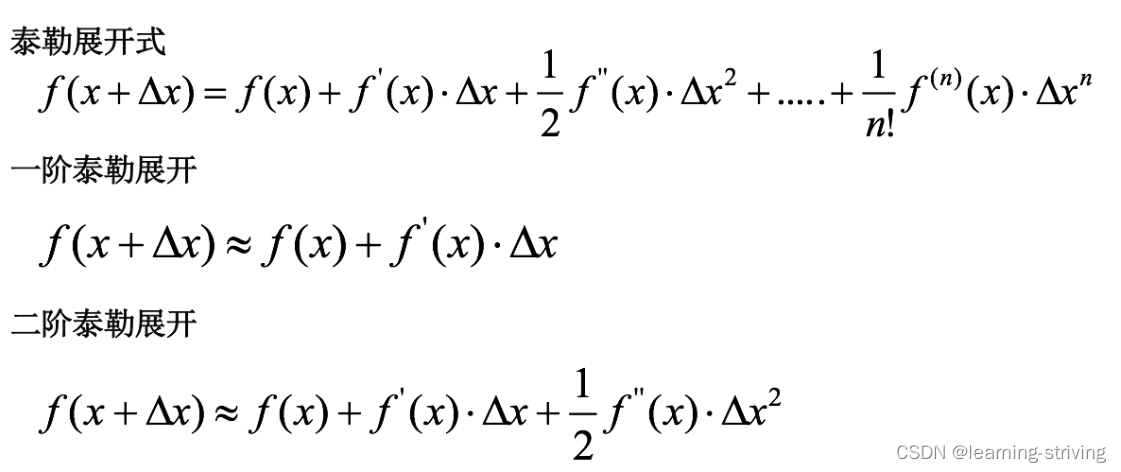
学习导航:http://xqnav.top

![[oeasy]python0051_ 转义_escape_字符_character_单引号_双引号_反引号_ 退格键](https://img-blog.csdnimg.cn/img_convert/5df40d17e1c9c8b4286963afc6cb5e06.png)