目录
一、层次分析法简介
举一个小例子:
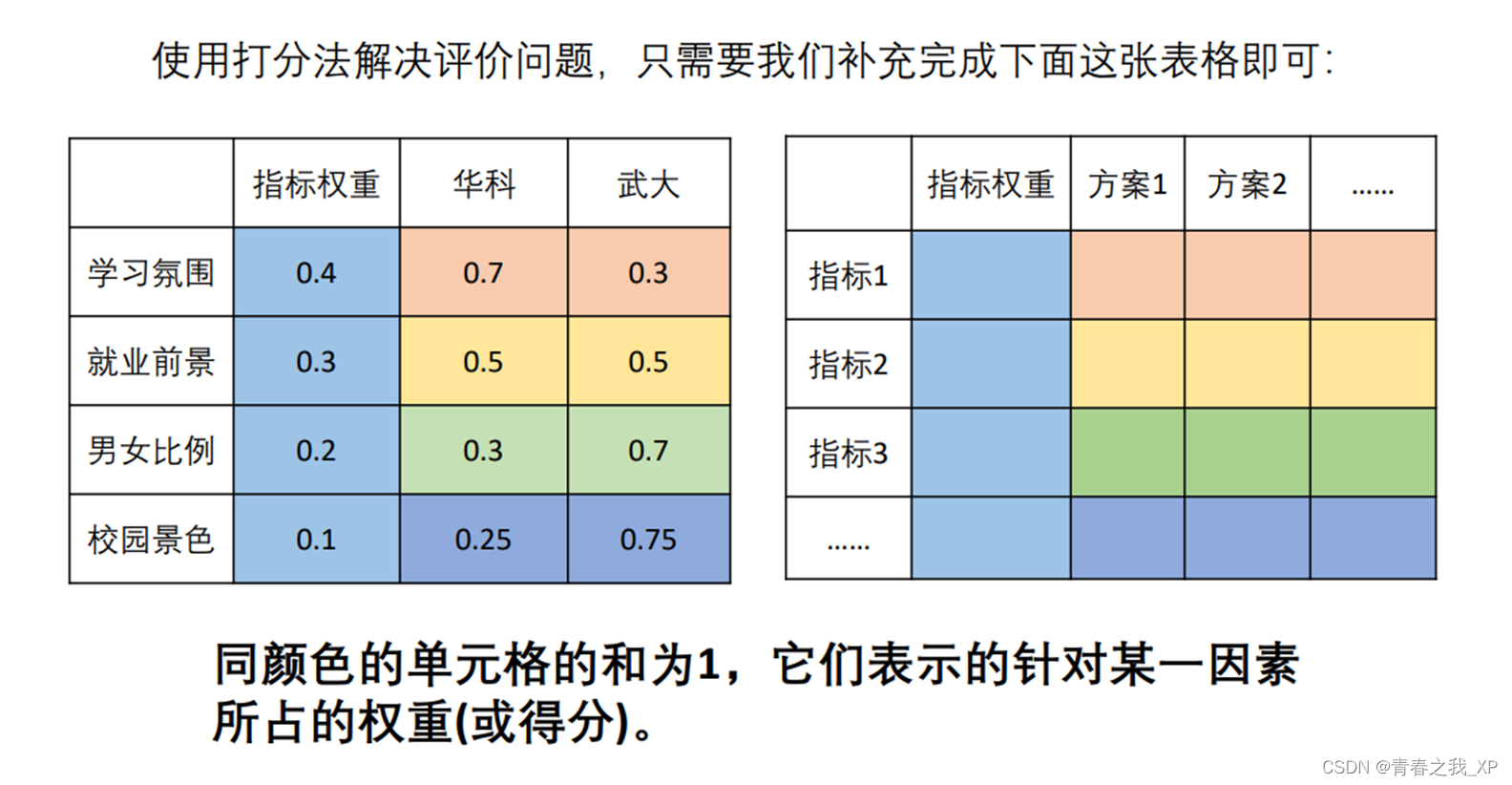
评价类问题可用打分解决,比如:小华高考结束后,在华科和武大两所学校之间做抉择。
评价类问题可用打分解决
二、层次分析法的步骤
(一)一道引出层次分析法的例题
(二)建立层次分析法的步骤
(1)第一步、建立层次结构模型
(2) 第二步、构造判断矩阵
(3)第三步、 求权重并做一致性检验
①计算最大特征值方法1:算术平均法
②计算最大特征值方法2:几何平均法
③计算最大特征值方法3:特征值法
三种方法结果综合分析:
(4)第四步、根据权重矩阵计算得分,并进行排序
三、总结
判断矩阵不满足一致性检验,CR>0.1,如何修正?
层次分析法的优点:
层次分析法的一些局限性:
层次分析法的适用情况:
一、层次分析法简介
层次分析法是建模比赛中最基础的模型之一,其主要用于解决评价类问题
(例如:选择哪种方案最好、哪位运动员或者员工表现的更优秀)
举一个小例子:

评价类问题可用打分解决,比如:小华高考结束后,在华科和武大两所学校之间做抉择。

评价类问题可用打分解决
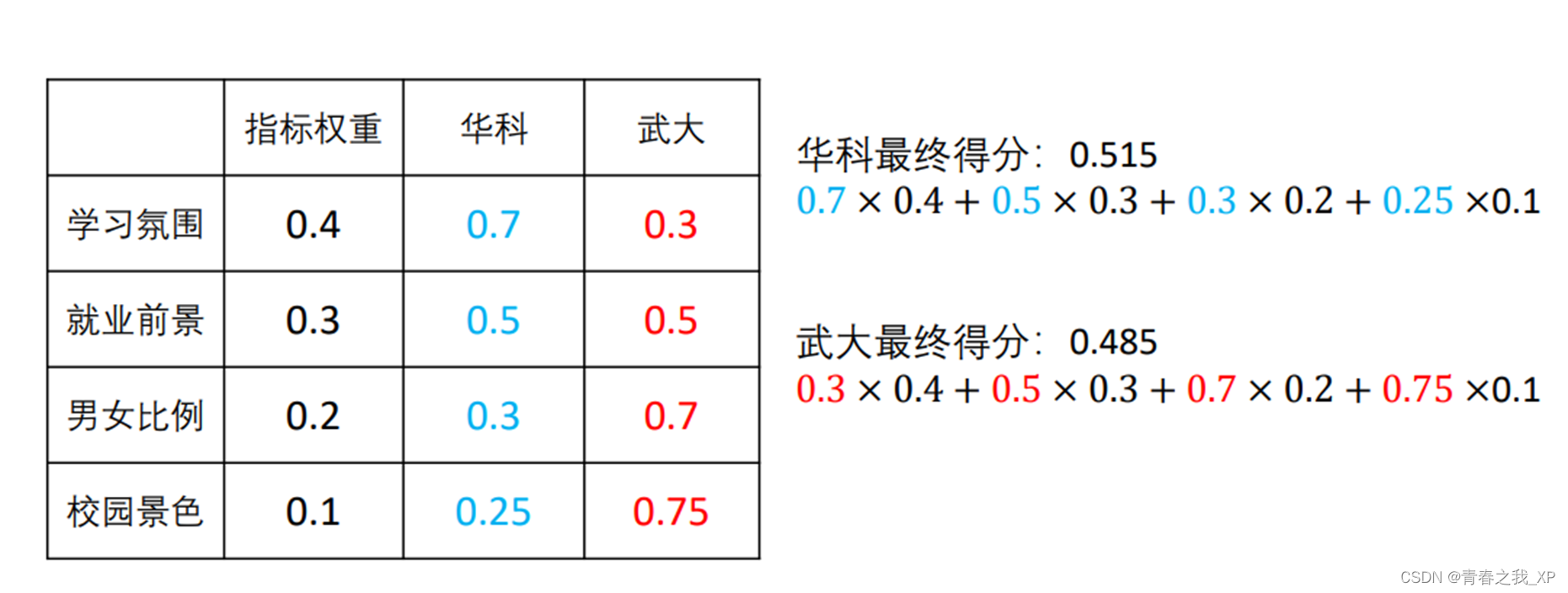
最终建议小华选择得分最高的一个学校:华科。
二、层次分析法的步骤
(一)一道引出层次分析法的例题
小华同学想出去旅游。在查阅了网上的攻略后,他初步选择了苏杭、北戴河和桂林三地之一作为目标景点。
请你确定评价指标、形成评价体系来为小华同学选择最佳的方案。
解决评价类问题,首先要想到以下三个问题:
① 我们评价的目标是什么?
② 我们为了达到这个目标有哪几种可选的方案?
③ 评价的准则或者说指标是什么?(我们根据什么东西来评价好坏)
解决评价类问题,大家首先要想到以下三个问题:
① 我们评价的目标是什么?
答:为小华同学选择最佳的旅游景点。
② 我们为了达到这个目标有哪几种可选的方案?
答:三种,分别是去苏杭、去北戴河和去桂林。
③ 评价的准则或者说指标是什么?(我们根据什么东西来评价好坏)
答:题目没给相关数据支撑,需要我们查阅相关的资料。
一般而言,前两个问题的答案是显而易见的,第三个问题的答案 需要我们根据题目中的背景材料、常识以及网上搜集到的参考资料进行结合,从中筛选出最合适的指标
脑洞:假如现在小华就在我们面前,我们要对他提哪些问题才能帮他合理地做决定?

问题: 一次性考虑这五个指标之间的关系,往往考虑不周。
解决方法: 两个两个指标进行比较,最终根据两两比较的结果来推算出权重。
目的:求权重!!!!!!
有同学可能会想,直接叫小华填好这张表不就完事啦~
这样往往比较片面和不周全 (隔一天问他答案可能就变了)
在确定影响某因素的诸因子在该因素中所占的比重时,遇到的主要困难 是这些比重常常不易定量化。此外,当影响某因素的因子较多时,直接考虑各因子对该因素有多大程度的影响时,常常会因考虑不周全、顾此 失彼而使决策者提出与他实际认为的重要性程度不相一致的数据,甚至 有可能提出一组隐含矛盾的数据。
——选自司守奎[kuí]老师的《数学建模算法与应用》
(二)建立层次分析法的步骤
(1)第一步、建立层次结构模型
解决评价类问题,大家首先要想到以下三个问题:
① 我们评价的目标是什么?
答:为小华同学选择最佳的旅游景点。
② 我们为了达到这个目标有哪几种可选的方案?
答:三种,分别是去苏杭、去北戴河和去桂林。
③ 评价的准则或者说指标是什么?(我们根据什么东西来评价好坏)
答:题目没给相关数据支撑,需要我们查阅相关的资料。
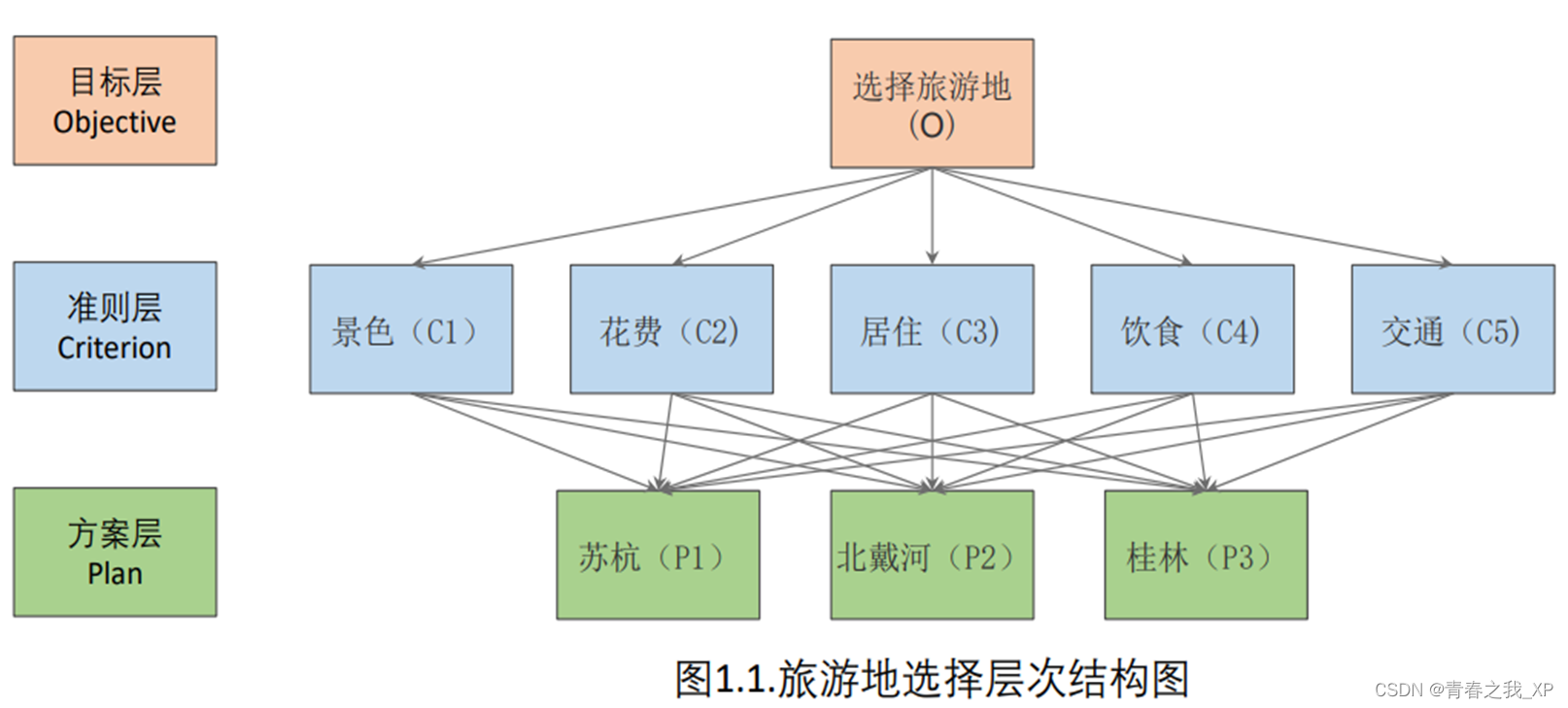
注意:如果你用到了层次分析法,那么这个层次结构图要放在你的建模论文中。
(2) 第二步、构造判断矩阵
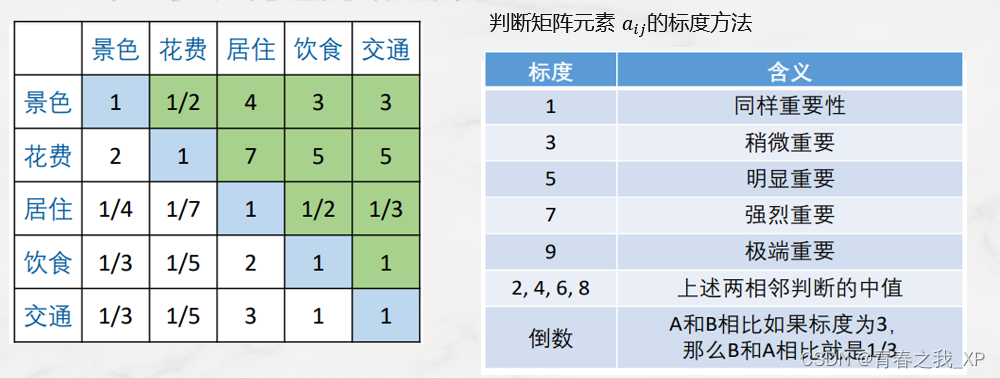



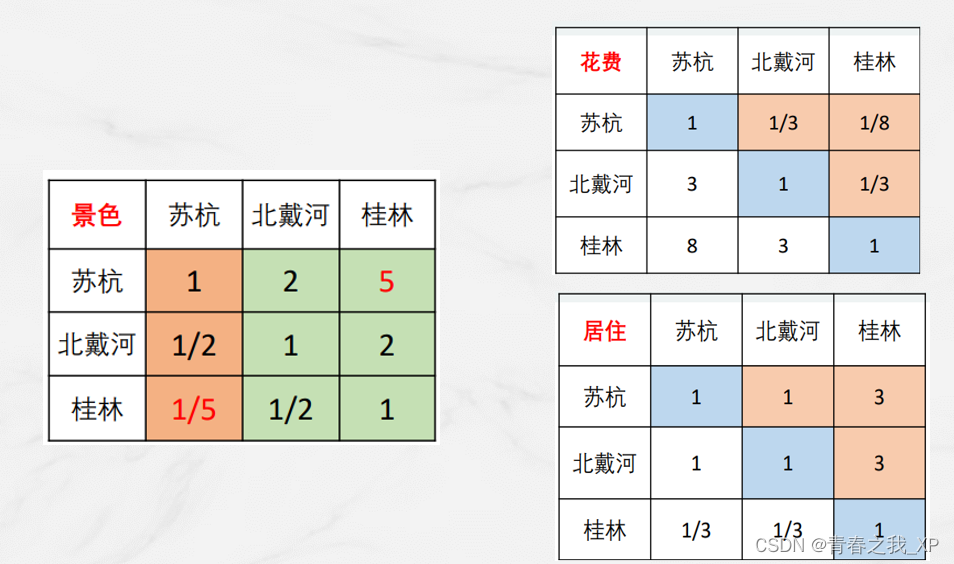
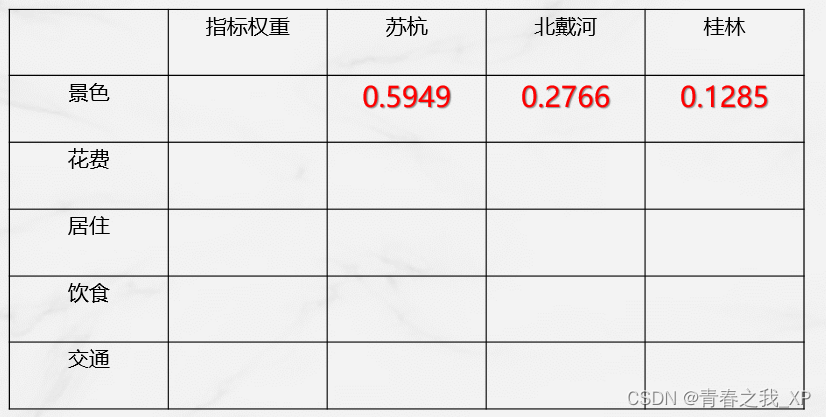
根据五个指标,分别构造出来的判断矩阵,如下:

(3)第三步、 求权重并做一致性检验
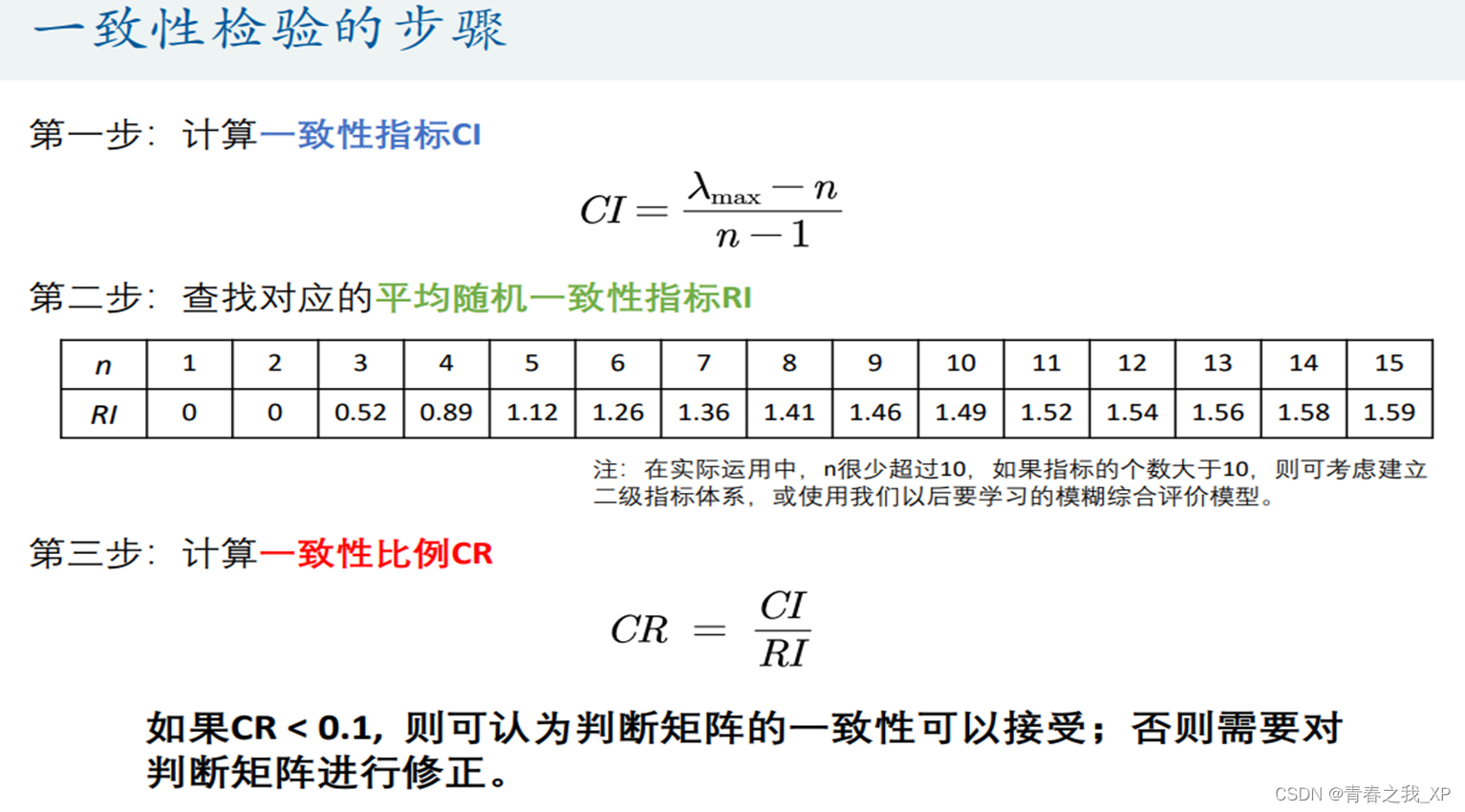
在使用判断矩阵求权重之前,必须对其进行一致性检验。


一致性检验的目的:为了检验各元素重要度之间的协调性,避免出现A比B重要,B比C重要,而C又比A重要这样的矛盾情况出现。
引理:n阶判断矩阵A为一致矩阵时,当且仅当最大特征值=n
n阶判断矩阵A非一致时,一定满足最大特征值>n
判断矩阵越不一致时,最大特征值与n相差就越大
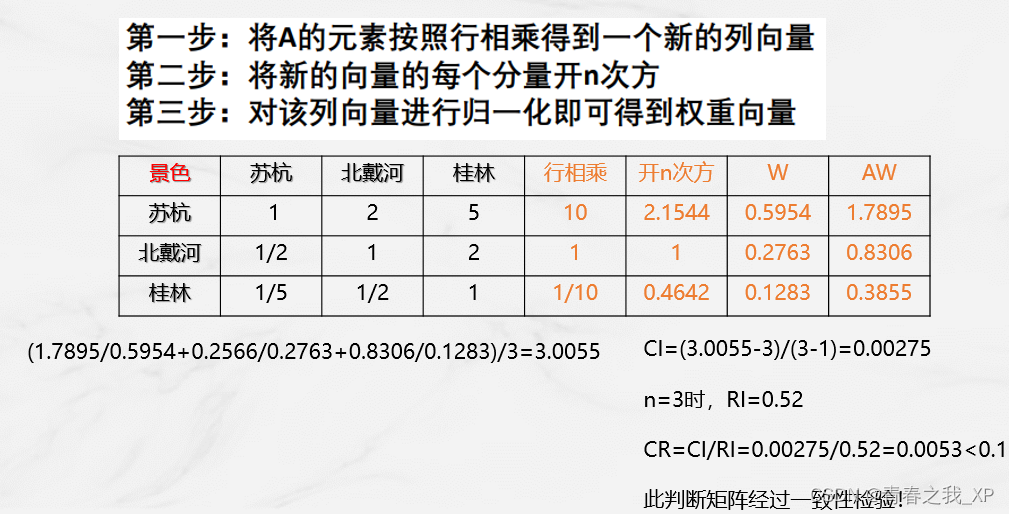
三种方法计算最大特征值:
①算术平均法(和积法)
②几何平均法(方根法)
③特征值法
①计算最大特征值方法1:算术平均法
第一步:将判断矩阵按照列归一化 (每一个元素除以其所在列的和)
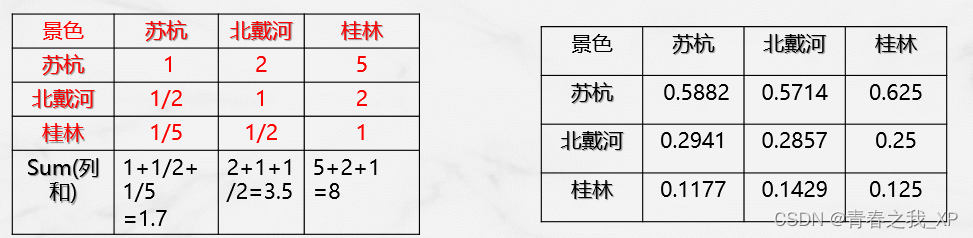
第二步:将归一化的各列按行求和
第二步:将相加后得到的向量中的每个元素除以n即可得到权重向量

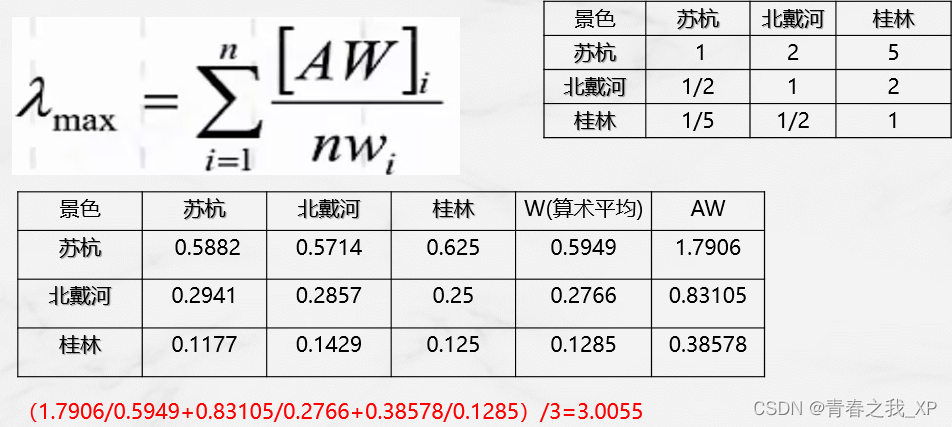

结果如下:
②计算最大特征值方法2:几何平均法
③计算最大特征值方法3:特征值法
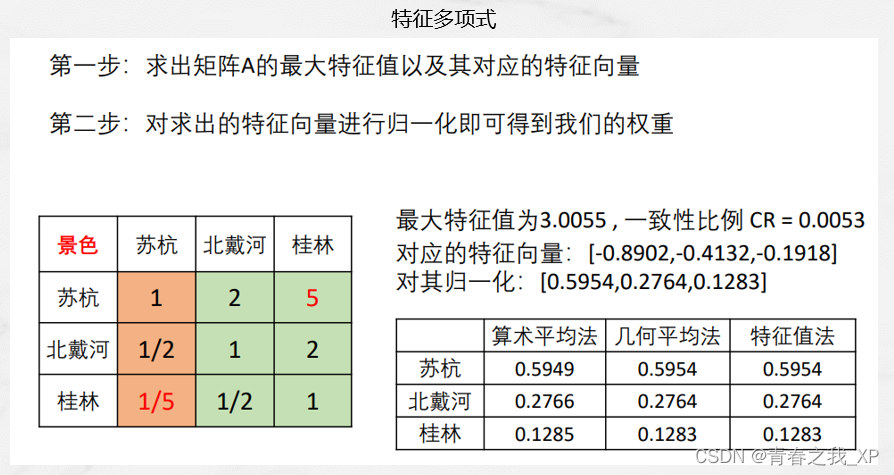
三种方法结果综合分析:

(4)第四步、根据权重矩阵计算得分,并进行排序
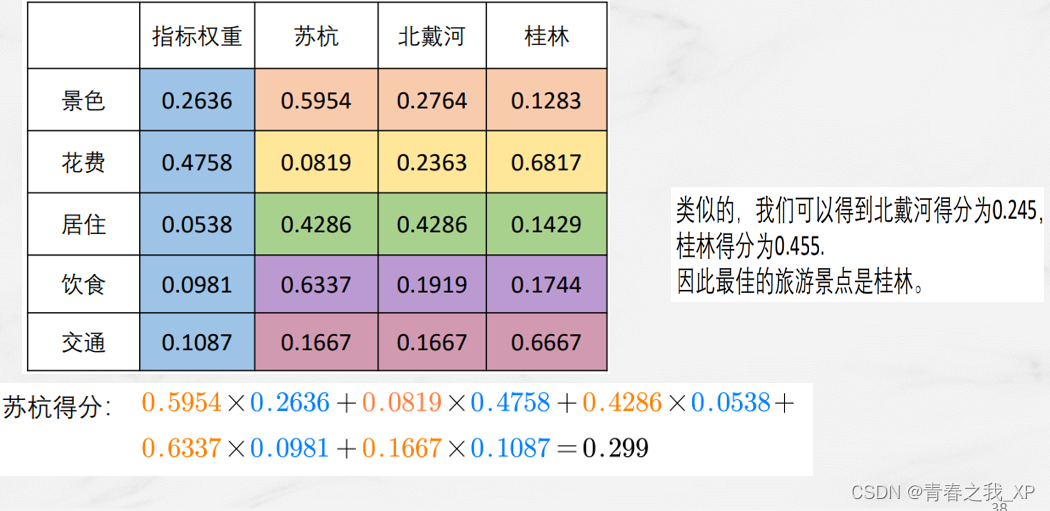
三、总结


判断矩阵不满足一致性检验,CR>0.1,如何修正?
1. 重新构建判断矩阵:请专家重新评估要素之间的相对重要程度,确保判断矩阵满足一致性要求。
2. 调整判断矩阵中的数据:对判断矩阵中不满足一致性的元素进行微调,以达到一致性。可以使用辅助软件(如 Yaahp、AHP-Online 等)提供的功能进行检查和处理。
3.降低判断矩阵阶数:如果判断矩阵的阶数过高,可以考虑降低其阶数,从而简化模型。这可以通过合并一些相关性较高的指标或子目标来实现。但要注意,降低阶数可能会影响分析结果的准确性。
往一致矩阵上调整 使一致矩阵各行成倍数关系
层次分析法的优点:
系统性:将对象视作系统,按照分解、比较、判断、综合的思维方式进行决策。成为继机理分析、统计分析之后发展起来的系统分析的重要工具;
实用性:定性与定量相结合,能处理许多用传统的最优化技术无法着手的实际问题,应用范围很广,同时,这种方法使得决策者与决策分析者能够相互沟通,决策者甚至可以直接应用它,这就增加了决策的有效性;
简洁性:计算简便,结果明确,具有中等文化程度的人即可以了解层次分析法的基本原理并掌握该法的基本步骤,容易被决策者了解和掌握。便于决策者直接了解和掌握。
层次分析法的一些局限性:
层次分析法的适用情况:
它适合用于以下几种情况:
1. 当决策问题涉及多个因素且这些因素之间存在层次关系时,可以使用层次分析法来理清各因素之间的关系,并确定各个层次的权重。
2. 当决策问题涉及到一些难以量化的因素时,层次分析法可以帮助我们将这些因素转化为可以比较的量化指标,从而进行决策。
3. 当决策问题需要考虑多方面的观点和意见时,层次分析法可以帮助我们综合各方的观点,形成统一的决策。
4. 当决策问题需要平衡多种目标和利益时,层次分析法可以帮助我们确定各个目标和利益的权重,以便找到最佳的平衡点。
总之,层次分析法适合于那些涉及多个因素、难以量化、需要考虑多方面观点和需要平衡多种目标和利益的决策问题。