给定一个候选人编号的集合 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。candidates 中的每个数字在每个组合中只能使用 一次 。注意：解集不能包含重复的组合。

示例 2:
输入: candidates = [2,5,2,1], target = 5,
输出:[[1,2,2],[5]]

class Solution {
    List<List<Integer>> res = new ArrayList<>();
    List<Integer> path = new ArrayList<>();
    int sum = 0;
    int[] used;
    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        Arrays.sort(candidates);
        used = new int[candidates.length];
        backtracking(candidates, 0, target);
        return res;
    }

    void backtracking(int[] candidates, int startIndex, int target){
        
        if(sum > target) return;
        if(sum == target){
            res.add(new ArrayList<>(path));
            return;
        }
        for(int i = startIndex;i < candidates.length;i++){
            if(i > 0 && candidates[i] == candidates[i - 1] && used[i - 1] == 0){
                continue;
            }
            path.add(candidates[i]);
            sum += candidates[i];
            used[i] = 1;
            backtracking(candidates, i + 1, target);
            path.remove(path.size() - 1);
            sum -= candidates[i];
            used[i] = 0;
        }
    }
}

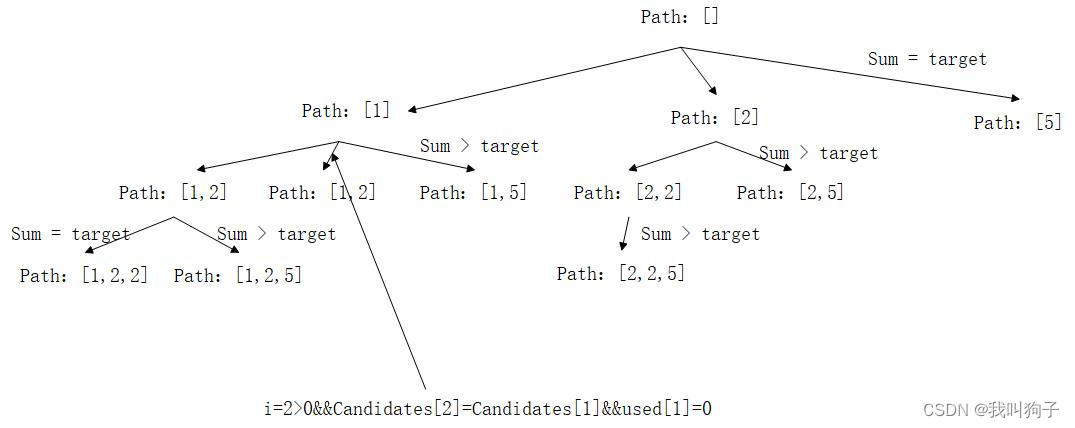
        这一题与组合总和I不同的是给出的数组中存在重复元素，可会导致重复的组合，注意组合中元素无顺序关系，即[1, 2]和[2, 1]是同一个组合，因此这一题去上一题唯一的区别是加上去重逻辑。如何去重？定义一个used数组，表示数组中的元素是否被使用，1表示被使用，0则没有被使用。之后将数组元素进行排序，并加入if(i > 0 && candidates[i] == candidates[i - 1] && used[i - 1] == 0)，即可完成去重操作，这行代码可以避免通过for循环横向添加元素，允许通过递归方式纵向添加元素。
        以上述示例说明代码的详细执行流程，首先定义ans集合收集所有符合条件的组合，path用于收集遍历过程中添加的元素，如果path中元素的组合符合条件，将其加入到ans集合中，定义sum表示path中元素和，定义used数组表示数组中元素是否在path中，combinationSum2中调用backtracking方法，最后返回ans集合。
        初始化used数组，并对数组进行排序，排序结果为[1, 2, 2, 5]，进入backtracking，sum为0，不满足两个if条件，进入for循环，i等于0，不满足if条件，将元素1加入到path中，path为[1]，used[0]等于1，sum等于1，递归进入下一个backtracking，sum等于1不满足if条件，进入for循环，startIndex为1，从下标1开始，显然不满足if条件，将元素2加入到path中，path为[1, 2]，used[1]等于1，sum等于3，递归进入下一个backtracking，sum等于3不满足两个if条件，进入for循环，startIndex为2，从下标2开始，显然不满足if条件，将元素2加入到backtracking中，path为[1, 2, 2]，used[2]等于1，sum等于5，递归进入下一个backtracking中，sum等于target，将[1, 2, 2]放入ans集合中，递归返回上一个backtracking，将元素2从path中移除，path为[1, 2]，used[2]等于0，sum等于3，for循环继续，i++，显然不满足if条件，将元素5放入path中，path为[1, 2, 5]，used[3]等于1，sum等于8，递归进入下一个backtracking，sum > target，递归返回上一个backtracking，将元素5从path中移除，path为[1, 2]，used[3]等于0，for循环继续，i++，等于数组长度，for循环结束，递归返回上一个backtracking，将元素2从path中移除，path为[1]，used[1]等于0，sum等于1，for循环继续，i++，candidates[2] = candidates[1]，并且used[1]等于0，满足if田间，跳过元素2，避免了for循环横向添加重复元素，i++，遍历元素5，将元素5加入到path中，path为[1, 5]，used[3]等于1，sum等于6，递归进入下一个backtracking，sum > target，递归返回上一个backtracking，将元素5从path中移除，path为[1]，used[3]等于0，sum等于1，for循环继续，i++，等于数组长度，for循环结束，递归返回最初的backtracking，将元素1从path中移除，path为空，used[0]等于0，sum等于0。如此重复即可得到所有符合条件的组合。
        下面给出上述代码执行的图示。