Hikyuu Quant Framework 是一款基于C++/Python的开源量化交易分析与研究工具,主要用于A股市场的交易策略分析与回测,目前不支持期货等,需要自行改造。
Hikyuu的目标
Hikyuu的最初目的是为了快速对A股全市场股票进行策略回测和验证,而不是“乌龟拖车”式的漫长等待。为了达成这个目标,Hikyuu除了使用 C++ 来实现快速的计算引擎外,还同时将交易概念进行了抽象和分割,可以自行根据需要进行构建、组合,既能快速重用也避免了复杂代码容易出错的问题。另外,因为部件策略都是统一的命名规则,还带来了一个额外的好处,也就是理论上可以方便进行策略部件级别的组合和探索,更加专注于某一方面策略的性能和影响,甚至使用AI去进行策略部件级别的挖掘,而不是仅仅用来挖掘因子,当然目前还没有实现,仍然需要继续前行与探索。
Hikyuu的性能和缺点
作者本人没有和其他回测框架进行过比较,但之前在知乎上有人做过对比,这里借用一下,大家有兴趣也可以自行搜索下“不同回测框架的比较”:


让作者汗颜,虽然个人其实觉得文档其实是有的,只不过更多的是API形式,而没有按使用场景去组织也没有提供更多的示例。另外,Hikyuu是对交易概念的抽象,要想真正用好 hikyuu,需要对“交易是如何赚钱”的有所了解,而不是仅仅只是低买高卖,这也是初入门时的门槛。所以,现在开始补文档,感觉任重道远,也欢迎大家加入星球共建。
即然提到了缺点,这里也说一下 Hikyuu 的缺点(虽然我很想只说优点)供大家更好的进行决策选择:
- 目前只支持国内A股市场,不支持期货等,但可以自行改造,hikyuu的核心计算引擎和数据存储是分离的
- 以探索性编程为主,并未提供相关的GUI,需要有一定的编程基础
- 回测是 onBar 且类向量化的方式,不是事件驱动型的。这是为了进行快速在全市场中进行探索而生的,虽然后续会加入事件驱动级别的回测进行,但目前尚未提供,只是列入计划。向量化的方式也决定了在回测时,通常不能使用前向复权进行测试(原理以后再说)。
Hikyuu的概念架构
这里并不会对Hikyuu进行价格进行详细的介绍,以后再逐一介绍,仅是让大家先有个初步了解,因为后面的示例中会经常出现一些缩写,这里主要让大家了解熟悉Hikyuu中常用缩写代表的含义。
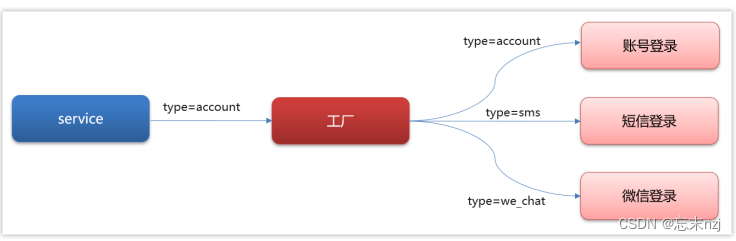
Hikyuu的概念架构如下图所示,其核心计算引擎包含了2个策略框架:单标的系统交易策略(SYS),投资组合策略(PF);9个策略部件:市场环境判断策略(EV)、系统有效条件(CN)、信号指示器(SG)、止损/止盈策略(ST/TP)、资金管理策略(MM)、盈利目标策略(PG)、移滑价差算法(SP)、交易对象选择策略(SE)。

Hikyuu项目地址
诚邀大家使劲点赞:
国内:https://gitee.com/fasiondog/hikyuu
国外:https://github.com/fasiondog/hikyuu
Hikyuu策略部件与示例公共仓库:
国内:https://gitee.com/fasiondog/hikyuu_hub
国外:https://github.com/fasiondog/hikyuu_hub