1、复数绘制极坐标图

# _*_ coding:UTF-8 _*_

import matplotlib.pyplot as plt
import numpy as np
 
# 定义复数数组
complexNums = [1.5 + 1.2j, 2.5 - 0.7j, -1.5 + 2.2j, -2.5 + 0.7j]
#1.5+1.2j=complex(1.5,1.2)
 
# 转换为极坐标
# 求解复数的模（模长）
modulus = np.abs(complexNums)
# 求解复数的相角（弧度表示）
angles = np.angle(complexNums)
 
# 绘制极坐标图
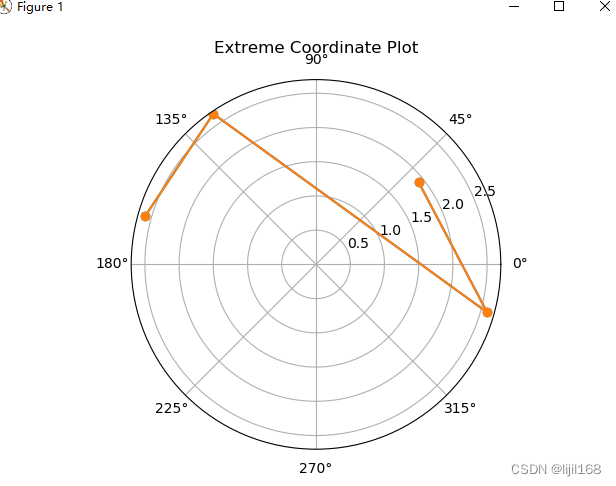
plt.polar(angles, modulus, 'o-')
 
# 设置极坐标图的标签和标题
plt.title('Extreme Coordinate Plot')
 
# 显示图形
plt.show()

2、动刚度的计算公式

动刚度为复数，有模和相位角（滞后角，与阻尼有关）

3、悬置动刚度的影响因素

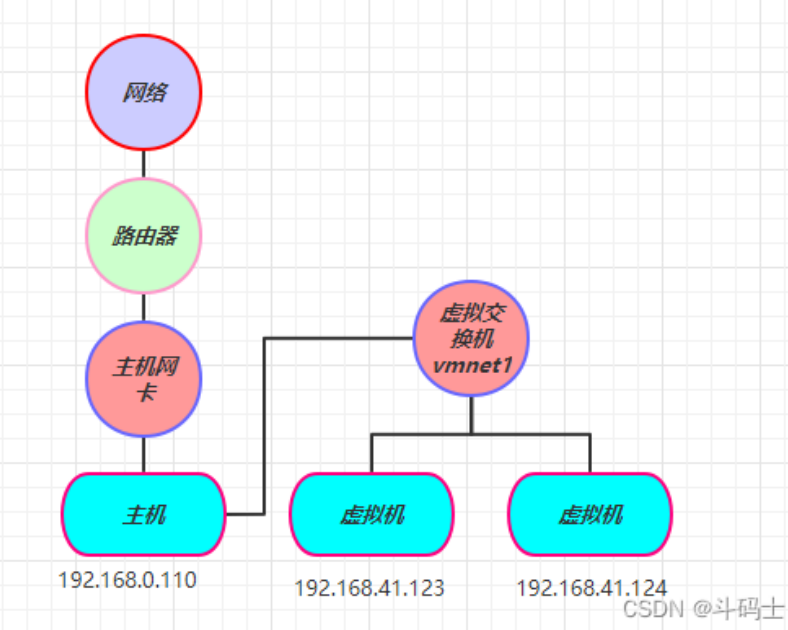
发动机悬置的动刚度和工作时的频率、预载荷、动态载荷的幅值有关，要确定准确的动刚度，需要对发动机工作时的悬置动刚度进行测试，对怠速时悬置动刚度，根据怠速时悬置点振动的频谱，由振动能量最大的频率来确定其动刚度，发动机怠速时，悬置振动主要是以3、6阶振动为主，频率较低，取静刚度的1.2~1.4倍作为动刚度进行计算，似乎是不准确的。

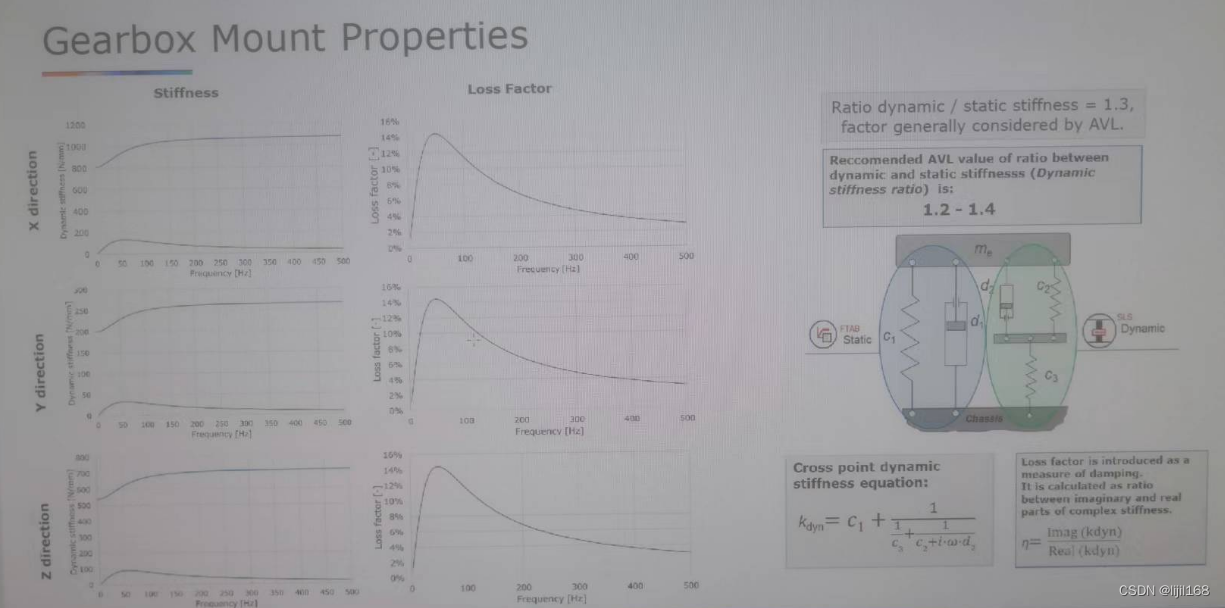
4、 AVL Excite 悬置动刚度的模拟

AVL Excite 悬置数学模型有几种，比较简单的一种为：用FTAB模拟静刚度，用SLS模拟动刚度，计算模型如下图，？？图中似乎没有考虑d1阻尼的影响。

def k_dyn(k1=199,k2=1,k3=60,d2=0.5):
    fi=np.linspace(0,500,501)
    wi=2*np.pi*fi
    #k1=199 #静刚度-1
    #k2=1
    #k3=60 #调动刚度
    #d2=0.5 #调动刚度
    kSLS=[1./(1./k3+1./complex(k2,w*d2)) for w in wi] #SLS动刚度
    kDyn=k1+np.array(kSLS)
    plt.subplot(1,2,1)
    plt.plot(fi,kDyn.real,kDyn.imag)
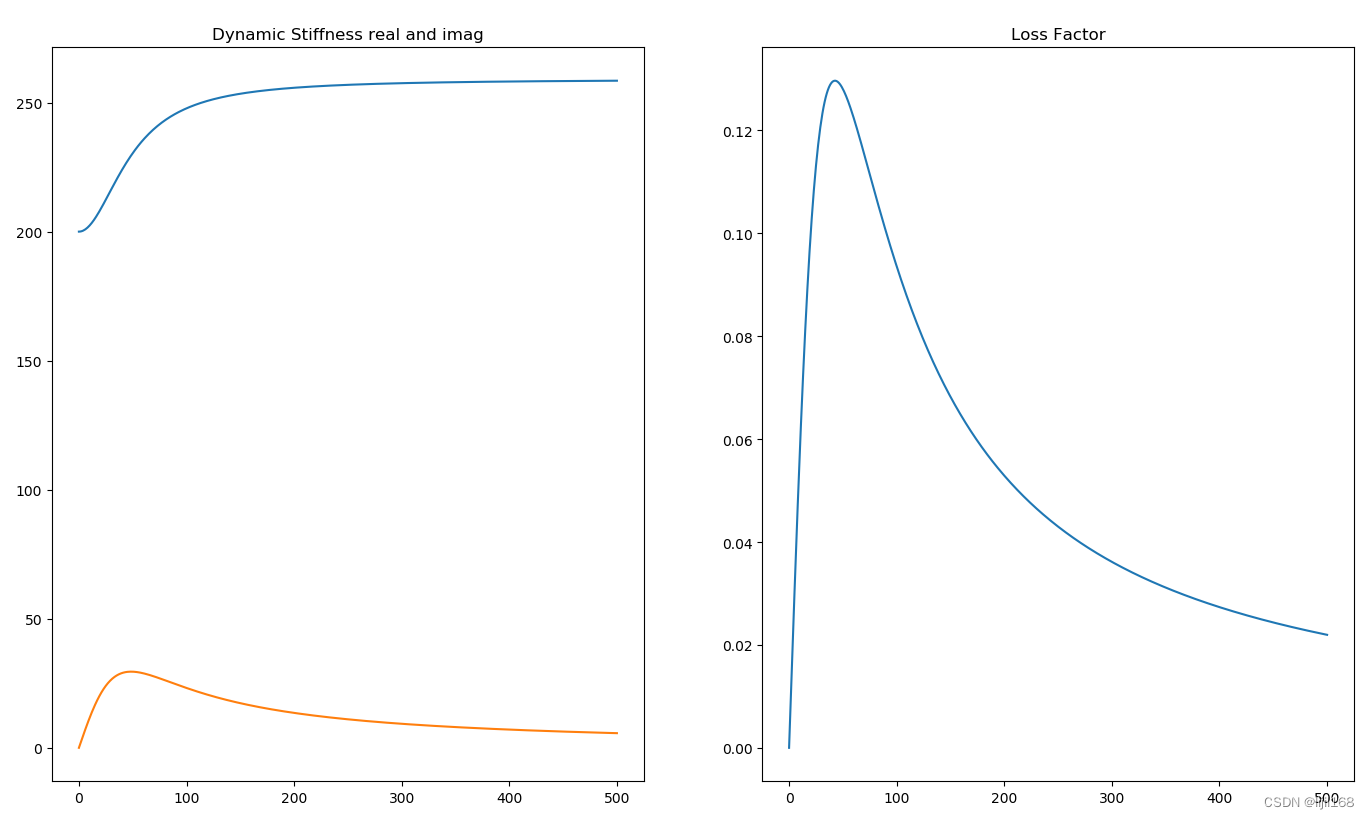
    plt.title('Dynamic Stiffness real and imag')
    plt.subplot(1,2,2)
    plt.plot(fi,kDyn.imag/kDyn.real) #Loss Factor tan(滞后角）~2阻尼比
    plt.title('Loss Factor')
    plt.show()

k_dyn(199,1,60,0.2)