1. 算法介绍

1.1 算法定义

  朴素贝叶斯分类（NBC）是以贝叶斯定理为基础并且假设特征条件之间相互独立的方法，先通过已给定的训练集，以特征词之间独立作为前提假设，学习从输入到输出的联合概率分布，再基于学习到的模型，输入x求出使得后验概率最大的输出y。

1.2 算法逻辑

对于算法的公式，不做过多的推导演算，此处希望以数据案例来做相应的解释。

首先，展示一下虚拟的数据结构：

此处使用流动性，动量，市值和贝塔四个层面的因子作为数据的属性特征，操作列做为分类特征，作为演示的案例数据。

目标是，测算流动性低，动量弱，市值大，贝塔高的标的对应的操作分类，也就是买入还是卖出。为此，以下分别展示了每一个分类下，对应的出现概率：

举例说明：特征为流动性低，方向为买入的概率计算方式为：首先筛选方向为买入的数据，对应有6条；其次在对应6条的数据中筛选流动性为低的数据，对应为2条。因此，对应的概率,2/6=0.33，依次类推，计算出其他分类和特征下对应的概率。

基于训练数据的统计，流动性低，动量弱，市值大，贝塔高的标的对应买入的联合概率(每种情况出现的概率的累乘)为：0.33*0.33*0.33*0.67 = 0.025,以此类推，对应卖出的联合概率为0.003，因为买入的联合概率大于卖出的联合概率，因此流动性低，动量弱，市值大，贝塔高的标的对应的操作分类为买入。案例对应的代码如下：

import pandas as pd
data_dict = {
    '流动性': {0: '低', 1: '中', 2: '高', 3: '低', 4: '中', 5: '高', 6: '低', 7: '中', 8: '高', 9: '低', 10: '中',
               11: '高'},
    '动量': {0: '强', 1: '弱', 2: '弱', 3: '强', 4: '强', 5: '弱', 6: '弱 ', 7: '强', 8: '弱 ', 9: '强', 10: '强',
             11: '强'},
    '市值': {0: '大', 1: '中', 2: '小', 3: '大', 4: '中', 5: '小', 6: '大', 7: '中', 8: '小', 9: '大', 10: '中',
             11: '小'},
    '贝塔': {0: '高', 1: '低', 2: '低', 3: '高', 4: '低', 5: '高', 6: '高', 7: '低', 8: '高', 9: '低', 10: '低',
             11: '低'},
    '操作': {0: '买入', 1: '卖出', 2: '买入', 3: '买入', 4: '卖出', 5: '买入', 6: '卖出', 7: '卖出', 8: '买入',
             9: '卖出', 10: '卖出', 11: '买入'}}
data = pd.DataFrame(data_dict)


def get_dir_data(dir, case):
    # 获取不同结果下，对应特征出现的概率
    data_list = []
    for key in case.keys():
        value = case.get(key)
        print(key, value)
        one_data = data.loc[data['操作'] == dir]
        goal_data = one_data.loc[one_data[key] == value]
        print(goal_data)
        out_dict = {'方向': dir, '特征': key + value, '概率': round(len(goal_data) / len(one_data), 4)}
        data_list.append(out_dict)
    return pd.DataFrame(x for x in data_list)


def jiont(value):
    # 计算对应的联合概率
    out = 1
    for a in value:
        out = out * a
    return out


# 对算法进行相应的介绍
case = {'流动性': '低', '动量': '弱', '市值': '大', '贝塔': '高'}
buy, sell = '买入', '卖出'
buy_data = get_dir_data(buy, case)
sell_data = get_dir_data(sell, case)
buy_rate = jiont(buy_data['概率'])
sell_rate = jiont(sell_data['概率'])

1.3 算法函数 

使用sklearn对应的MultinomialNB()函数，由于某一特征属性下对应的分类概率可能为0，进而对整体的联合概率产生影响，因此，考虑在计算概率的时候使用拉普拉斯平滑，对应参数为alpha。

from sklearn.naive_bayes import MultinomialNB
model = MultinomialNB(alpha=1)

1.4 算法评价

朴素贝叶斯算法常用于新闻，电影以及邮件的标签分类，其主要有以下三个优点：

1. 稳定的分类效率

2. 算法比较简单，数据缺失对算法的影响较低

3. 分类的准确度高，速度比较快

尽管朴素贝叶斯的分类功能非常强大，但是其也有一个比较致命的缺点：要求各个属性特征之间均为独立，在实际的数据中非常难满足。如果数据的属性特征存在一定的交集，对分类结果准确度的影响会非常大。

2.算法实例

还是以算法逻辑对应的数据源data为例。

首选，对数据进行相应的特征提取与转换，sklearn有相应的函数（本文的数据没有找到合适的转换），因此使用自定义的函数来进行转换。

def value_transform(one_col):
    # 将原始数据单列的数据按照分类进行转换
    values_list = one_col.drop_duplicates().tolist()
    num_list = [x for x in range(len(values_list))]
    transform_dict = {}
    for x in range(len(values_list)):
        transform_dict[values_list[x]] = num_list[x]
    transform_list = [transform_dict.get(x) for x in one_col]
    return transform_list


def data_transform(data_set):
    # 对原始数据进行相应的转换
    col_list = data_set.columns
    new_data = pd.DataFrame()
    for col_name in col_list:
        new_data[col_name] = value_transform(data_set[col_name])
    return new_data

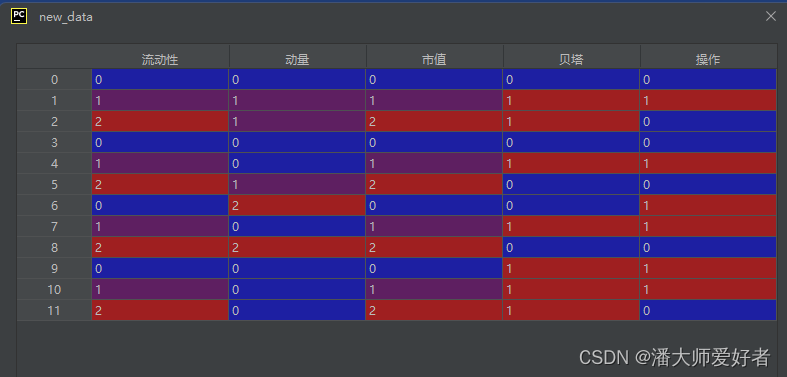
# 特征提取与转换
new_data = data_transform(data)

对应的结果为：

 然后选择需要的特征数据，并进行训练数据和检验数据的分割：

# 选择需要的特征数据，并切割训练数据和检验数据
from sklearn.naive_bayes import MultinomialNB
from sklearn.model_selection import train_test_split
x = new_data.loc[:, ['流动性', '动量', '市值', '贝塔']]
y = new_data['操作']
X_train, X_test, y_train, y_test = train_test_split(x, y, test_size=0.8, random_state=len(data))

建模，导入数据进行训练，然后进行相应的预测，并对预测结果和实际结果进行打分比较：

# 模型预测
model = MultinomialNB(alpha=1)
model.fit(X_train, y_train)
predictions = model.predict(X_test)

# 模型评价
score_value = round(model.score(X_test, y_test), 4)

对应score_value的值为0.4。说明整体的预测效果并不好，毕竟数据是虚拟的。当然，即使是真实的数据，想要得到一个比较好的结果也是比较苦难的。本文重点是介绍算法的逻辑和运用步骤，对于参数优化以及模型迭代，笔者力之所不能及。

本期分享到此结束，有何问题欢迎随时沟通！