目录
- 1.背景
- 2.算法原理
- 2.1算法思想
- 2.2算法过程
- 3.结果展示
- 4.参考文献
- 5.代码获取
1.背景
2024年,Y Fu受到自然界中鹭鹰生存行为启发,提出了鹭鹰优化算法(Secretary Bird Optimization Algorithm, SBOA)。


2.算法原理
2.1算法思想
SBOA生存需要不断地寻找猎物和躲避捕食者的追捕,探索阶段模拟鹭鹰捕食蛇,而开发阶段模拟鹭鹰逃离捕食者。在这个阶段,鹭鹰观察环境,选择最合适的方式到达安全的避难所。

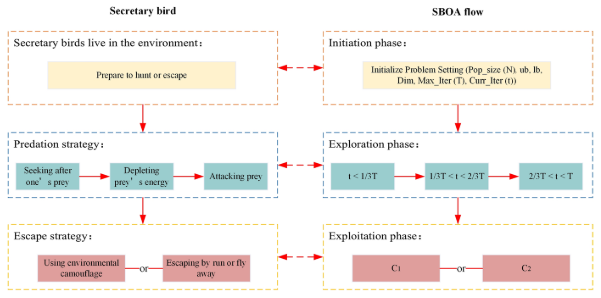
2.2算法过程
鹭鹰捕猎策略(探索阶段)
鹭鹰以蛇为食时的捕猎行为通常分为三个阶段:寻找猎物、消耗猎物和攻击猎物。整个捕食过程分为三个相等的时间间隔,分别对应鹭鹰捕食的三个阶段:寻找猎物、消耗猎物和攻击猎物。
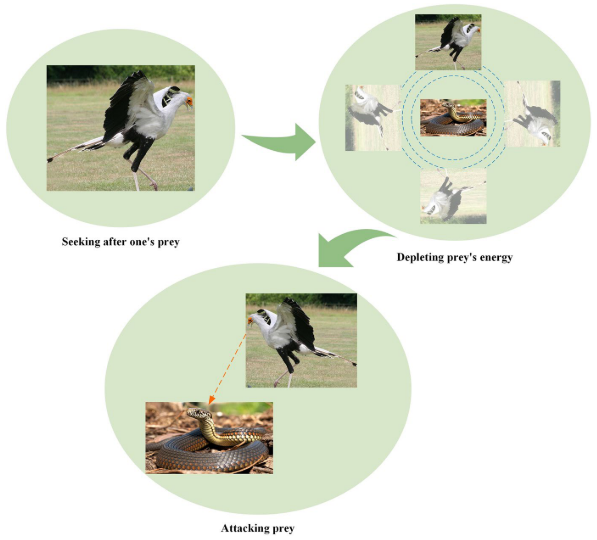
寻找猎物阶段的位置更新:
W
h
i
l
e
t
<
1
3
T
,
x
i
,
j
n
e
w
P
1
=
x
i
,
j
+
(
x
r
a
n
d
o
m
1
−
x
r
a
n
d
o
m
2
)
×
R
1
X
i
=
{
X
i
n
e
w
,
P
1
,
i
f
F
i
n
e
w
,
P
1
<
F
i
X
i
,
e
l
s
e
(1)
While t<\frac{1}{3}T,x_{i,j}^{new P1}=x_{i,j}+\left(x_{random_1}-x_{random_2}\right)\times R_{1}\\ X_i=\left\{\begin{array}{l}X_i^{new,P1},if F_i^{new,P1}<F_i\\X_i, else\end{array}\right.\tag{1}
Whilet<31T,xi,jnewP1=xi,j+(xrandom1−xrandom2)×R1Xi={Xinew,P1,ifFinew,P1<FiXi,else(1)
在消耗猎物阶段,引入布朗运动(RB)来模拟鹭鹰的随机运动,捕食阶段的位置更新:
R
B
=
r
a
n
d
n
(
1
,
D
i
m
)
W
h
i
l
e
1
3
T
<
t
<
2
3
T
,
x
i
,
j
n
e
w
P
1
=
x
b
e
s
t
+
exp
(
(
t
/
T
)
∧
4
)
×
(
R
B
−
0.5
)
×
(
x
b
e
s
t
−
x
i
,
j
)
X
i
=
{
X
i
n
e
w
,
P
1
,
i
f
F
i
n
e
w
,
P
1
<
F
i
X
i
,
e
l
s
e
(2)
RB=randn(1,Dim)\\ While \frac{1}{3}T<t<\frac{2}{3}T, x_{i,j}^{new P1}=x_{best}+\exp\left((t/T)\wedge4\right)\times(RB-0.5)\times\left(x_{best}-x_{i,j}\right)\\ X_{i}=\left\{\begin{array}{l}{{X_{i}^{new,P1},if F_{i}^{new,P1}<F_{i}}}\\{{X_{i}, else}}\end{array}\right.\tag{2}
RB=randn(1,Dim)While31T<t<32T,xi,jnewP1=xbest+exp((t/T)∧4)×(RB−0.5)×(xbest−xi,j)Xi={Xinew,P1,ifFinew,P1<FiXi,else(2)
鹭鹰在攻击猎物阶段的位置更新:
W
h
i
l
e
t
>
2
3
T
,
x
i
,
j
n
e
w
P
1
=
x
b
e
s
t
+
(
(
1
−
t
T
)
∧
(
2
×
t
T
)
)
×
x
i
,
j
×
R
L
X
i
=
{
X
i
n
e
w
,
P
1
,
i
f
F
i
n
e
w
,
P
1
<
F
i
X
i
,
e
l
s
e
(3)
While t>\frac{2}{3}T, x_{i,j}^{new P1}=x_{best}+\left(\left(1-\frac{t}{T}\right)\wedge\left(2\times\frac{t}{T}\right)\right)\times x_{i,j}\times RL\\ X_i=\left\{\begin{array}{ll}X_i^{new,P1},if F_i^{new,P1}<F_i\\X_i, else\end{array}\right.\tag{3}
Whilet>32T,xi,jnewP1=xbest+((1−Tt)∧(2×Tt))×xi,j×RLXi={Xinew,P1,ifFinew,P1<FiXi,else(3)
为了提高算法的优化精度,作者使用加权Levy飞行:
R
L
=
0.5
×
L
e
v
y
(
D
i
m
)
(4)
\mathrm{RL}=0.5\times Levy(Dim)\tag{4}
RL=0.5×Levy(Dim)(4)
鹭鹰逃生策略(开发阶段)
当遇到这些威胁时,鹭鹰通常采用各种逃避策略来保护自己或它们的食物。这些策略大致可以分为两大类,第一种策略是逃跑或快速奔跑,第二种策略是伪装。
其中C1代表第一种策略,C2代表第二种策略:
x
i
,
j
n
e
w
,
P
2
=
{
C
1
:
x
b
e
s
t
+
(
2
×
R
B
−
1
)
×
(
1
−
t
T
)
2
×
x
i
,
j
,
i
f
r
a
n
d
<
r
i
C
2
:
x
i
,
j
+
R
2
×
(
x
r
a
n
d
o
m
−
K
×
x
i
,
j
)
,
e
l
s
e
X
i
=
{
X
i
n
e
w
,
P
2
,
i
f
F
i
n
e
w
,
P
2
<
F
i
(5)
\left.x_{i,j}^{new,P2}=\left\{\begin{array}{l}C_{1}:x_{best}+(2\times RB-1)\times\left(1-\frac{t}{T}\right)^{2}\times x_{i,j},if r and <r_{i}\\C_{2}:x_{i,j}+R_{2}\times\left(x_{random}-K\times x_{i,j}\right),else\end{array}\right.\right.\\X_{i}=\left\{\begin{array}{l}X_{i}^{new,P2},if F_{i}^{new,P2}<F_{i}\end{array}\right.\tag{5}
xi,jnew,P2={C1:xbest+(2×RB−1)×(1−Tt)2×xi,j,ifrand<riC2:xi,j+R2×(xrandom−K×xi,j),elseXi={Xinew,P2,ifFinew,P2<Fi(5)
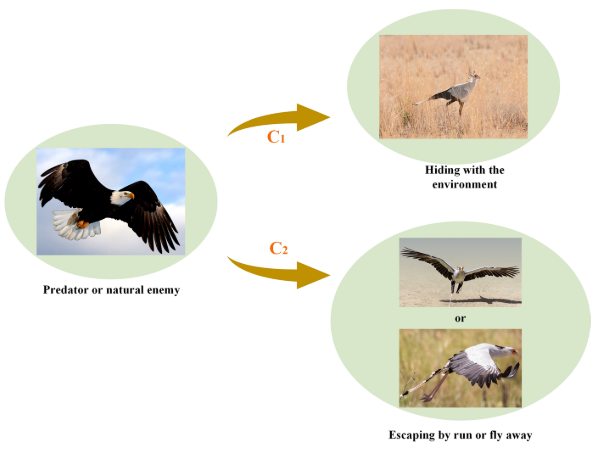
参数K表示整数1或2的随机选择:
K
=
r
o
u
n
d
(
1
+
r
a
n
d
(
1
,
1
)
)
(6)
K=round(1+rand(1,1))\tag{6}
K=round(1+rand(1,1))(6)
伪代码

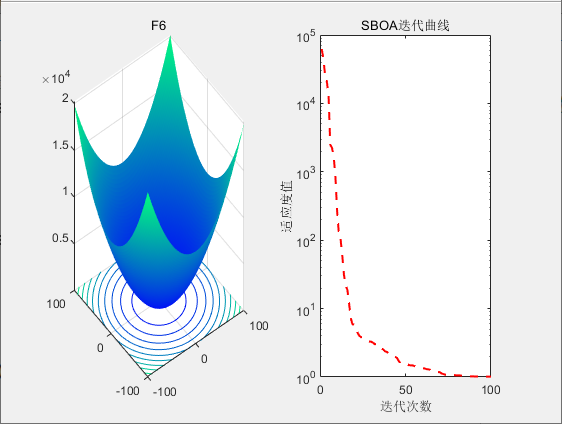
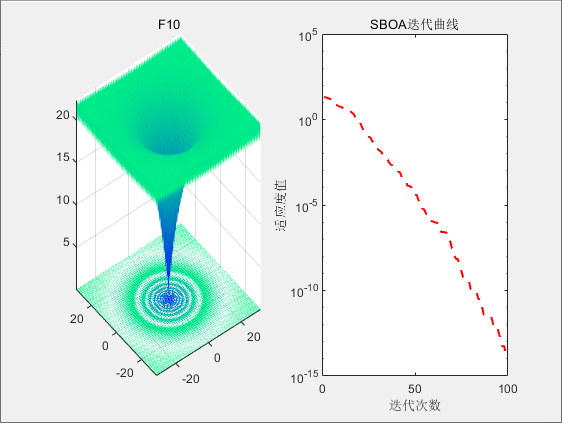
3.结果展示
4.参考文献
[1] Fu Y, Liu D, Chen J, et al. Secretary bird optimization algorithm: a new metaheuristic for solving global optimization problems[J]. Artificial Intelligence Review, 2024, 57(5): 1-102.
5.代码获取
资源清单