LeetCode 105.从前序与中序遍历序列构造二叉树

1、题目

题目链接：105. 从前序与中序遍历序列构造二叉树
给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例 1:

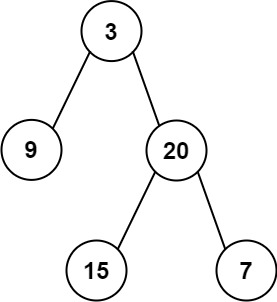
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

示例 2:

输入: preorder = [-1], inorder = [-1]
输出: [-1]

提示:

• 1 <= preorder.length <= 3000
• inorder.length == preorder.length
• -3000 <= preorder[i], inorder[i] <= 3000
• preorder 和 inorder 均 无重复 元素
• inorder 均出现在 preorder
• preorder 保证 为二叉树的前序遍历序列
• inorder 保证 为二叉树的中序遍历序列

2、递归

思路

二叉树前序遍历的顺序为：
先遍历根节点；
随后递归地遍历左子树；
最后递归地遍历右子树。
二叉树中序遍历的顺序为：
先递归地遍历左子树；
随后遍历根节点；
最后递归地遍历右子树。
在「递归」地遍历某个子树的过程中，我们也是将这颗子树看成一颗全新的树，按照上述的顺序进行遍历。挖掘「前序遍历」和「中序遍历」的性质，我们就可以得出本题的做法。

代码

class Solution {
private:
    unordered_map<int, int> index;

public:
    TreeNode* myBuildTree(const vector<int>& preorder, const vector<int>& inorder, int preorder_left, int preorder_right, int inorder_left, int inorder_right) {
        if (preorder_left > preorder_right) {
            return nullptr;
        }
        
        // 前序遍历中的第一个节点就是根节点
        int preorder_root = preorder_left;
        // 在中序遍历中定位根节点
        int inorder_root = index[preorder[preorder_root]];
        
        // 先把根节点建立出来
        TreeNode* root = new TreeNode(preorder[preorder_root]);
        // 得到左子树中的节点数目
        int size_left_subtree = inorder_root - inorder_left;
        // 递归地构造左子树，并连接到根节点
        // 先序遍历中「从 左边界+1 开始的 size_left_subtree」个元素就对应了中序遍历中「从 左边界 开始到 根节点定位-1」的元素
        root->left = myBuildTree(preorder, inorder, preorder_left + 1, preorder_left + size_left_subtree, inorder_left, inorder_root - 1);
        // 递归地构造右子树，并连接到根节点
        // 先序遍历中「从 左边界+1+左子树节点数目 开始到 右边界」的元素就对应了中序遍历中「从 根节点定位+1 到 右边界」的元素
        root->right = myBuildTree(preorder, inorder, preorder_left + size_left_subtree + 1, preorder_right, inorder_root + 1, inorder_right);
        return root;
    }

    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        int n = preorder.size();
        // 构造哈希映射，帮助我们快速定位根节点
        for (int i = 0; i < n; ++i) {
            index[inorder[i]] = i;
        }
        return myBuildTree(preorder, inorder, 0, n - 1, 0, n - 1);
    }
};

复杂度分析

• 时间复杂度: O(n)
• 空间复杂度: O(n)

3、递归（带日志）

思路

带日志的版本C++代码如下： （带日志的版本仅用于调试，不要在leetcode上提交，会超时）

代码

class Solution {
private:
        TreeNode* traversal (vector<int>& inorder, int inorderBegin, int inorderEnd, vector<int>& preorder, int preorderBegin, int preorderEnd) {
        if (preorderBegin == preorderEnd) return NULL;

        int rootValue = preorder[preorderBegin]; // 注意用preorderBegin 不要用0
        TreeNode* root = new TreeNode(rootValue);

        if (preorderEnd - preorderBegin == 1) return root;

        int delimiterIndex;
        for (delimiterIndex = inorderBegin; delimiterIndex < inorderEnd; delimiterIndex++) {
            if (inorder[delimiterIndex] == rootValue) break;
        }
        // 切割中序数组
        // 中序左区间，左闭右开[leftInorderBegin, leftInorderEnd)
        int leftInorderBegin = inorderBegin;
        int leftInorderEnd = delimiterIndex;
        // 中序右区间，左闭右开[rightInorderBegin, rightInorderEnd)
        int rightInorderBegin = delimiterIndex + 1;
        int rightInorderEnd = inorderEnd;

        // 切割前序数组
        // 前序左区间，左闭右开[leftPreorderBegin, leftPreorderEnd)
        int leftPreorderBegin =  preorderBegin + 1;
        int leftPreorderEnd = preorderBegin + 1 + delimiterIndex - inorderBegin; // 终止位置是起始位置加上中序左区间的大小size
        // 前序右区间, 左闭右开[rightPreorderBegin, rightPreorderEnd)
        int rightPreorderBegin = preorderBegin + 1 + (delimiterIndex - inorderBegin);
        int rightPreorderEnd = preorderEnd;

        cout << "----------" << endl;
        cout << "leftInorder :";
        for (int i = leftInorderBegin; i < leftInorderEnd; i++) {
            cout << inorder[i] << " ";
        }
        cout << endl;

        cout << "rightInorder :";
        for (int i = rightInorderBegin; i < rightInorderEnd; i++) {
            cout << inorder[i] << " ";
        }
        cout << endl;

        cout << "leftPreorder :";
        for (int i = leftPreorderBegin; i < leftPreorderEnd; i++) {
            cout << preorder[i] << " ";
        }
        cout << endl;

        cout << "rightPreorder :";
        for (int i = rightPreorderBegin; i < rightPreorderEnd; i++) {
            cout << preorder[i] << " ";
        }
        cout << endl;


        root->left = traversal(inorder, leftInorderBegin, leftInorderEnd,  preorder, leftPreorderBegin, leftPreorderEnd);
        root->right = traversal(inorder, rightInorderBegin, rightInorderEnd, preorder, rightPreorderBegin, rightPreorderEnd);

        return root;
    }

public:
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        if (inorder.size() == 0 || preorder.size() == 0) return NULL;
        return traversal(inorder, 0, inorder.size(), preorder, 0, preorder.size());

    }
};

复杂度分析

• 时间复杂度: O(n)
• 空间复杂度: O(n)

4、递归

思路

代码

class Solution {
private:
        TreeNode* traversal (vector<int>& inorder, int inorderBegin, int inorderEnd, vector<int>& preorder, int preorderBegin, int preorderEnd) {
        if (preorderBegin == preorderEnd) return NULL;

        int rootValue = preorder[preorderBegin]; // 注意用preorderBegin 不要用0
        TreeNode* root = new TreeNode(rootValue);

        if (preorderEnd - preorderBegin == 1) return root;

        int delimiterIndex;
        for (delimiterIndex = inorderBegin; delimiterIndex < inorderEnd; delimiterIndex++) {
            if (inorder[delimiterIndex] == rootValue) break;
        }
        // 切割中序数组
        // 中序左区间，左闭右开[leftInorderBegin, leftInorderEnd)
        int leftInorderBegin = inorderBegin;
        int leftInorderEnd = delimiterIndex;
        // 中序右区间，左闭右开[rightInorderBegin, rightInorderEnd)
        int rightInorderBegin = delimiterIndex + 1;
        int rightInorderEnd = inorderEnd;

        // 切割前序数组
        // 前序左区间，左闭右开[leftPreorderBegin, leftPreorderEnd)
        int leftPreorderBegin =  preorderBegin + 1;
        int leftPreorderEnd = preorderBegin + 1 + delimiterIndex - inorderBegin; // 终止位置是起始位置加上中序左区间的大小size
        // 前序右区间, 左闭右开[rightPreorderBegin, rightPreorderEnd)
        int rightPreorderBegin = preorderBegin + 1 + (delimiterIndex - inorderBegin);
        int rightPreorderEnd = preorderEnd;

        root->left = traversal(inorder, leftInorderBegin, leftInorderEnd,  preorder, leftPreorderBegin, leftPreorderEnd);
        root->right = traversal(inorder, rightInorderBegin, rightInorderEnd, preorder, rightPreorderBegin, rightPreorderEnd);

        return root;
    }

public:
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        if (inorder.size() == 0 || preorder.size() == 0) return NULL;

        // 参数坚持左闭右开的原则
        return traversal(inorder, 0, inorder.size(), preorder, 0, preorder.size());
    }
};

复杂度分析

• 时间复杂度: O(n)
• 空间复杂度: O(n)

5、迭代

思路

代码

class Solution {
public:
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        if (!preorder.size()) {
            return nullptr;
        }
        TreeNode* root = new TreeNode(preorder[0]);
        stack<TreeNode*> stk;
        stk.push(root);
        int inorderIndex = 0;
        for (int i = 1; i < preorder.size(); ++i) {
            int preorderVal = preorder[i];
            TreeNode* node = stk.top();
            // 如果栈顶节点的值不等于中序遍历的当前值
            if (node->val != inorder[inorderIndex]) {
                // 则当前节点是栈顶节点的左子节点
                node->left = new TreeNode(preorderVal);
                // 将左子节点压入栈中
                stk.push(node->left);
            }
            else {
                // 否则，不断弹出栈顶节点，直到栈顶节点的值不等于中序遍历的当前值
                while (!stk.empty() && stk.top()->val == inorder[inorderIndex]) {
                    node = stk.top();
                    stk.pop();
                    ++inorderIndex;
                }
                // 当前节点是栈顶节点的右子节点
                node->right = new TreeNode(preorderVal);
                // 将右子节点压入栈中
                stk.push(node->right);
            }
        }
        return root;
    }
};

复杂度分析

• 时间复杂度: O(n)
• 空间复杂度: O(n)