一、unordered_set、unordered_map的介绍

1.unordered_set、unordered_map的底层是哈希表，哈希表是一种关联式容器（与前面的二叉搜索树、AVL树、红黑树一样，数据与数据之间有很强的关联性）
2.单向迭代器（map、set是双向迭代器）
3.哈希表的查找顺序是O（1），性能比红黑树（logn）好一些（在数据接近与有序的情况下与哈希表一样）。

二、哈希表的建立方法

2.1闭散列

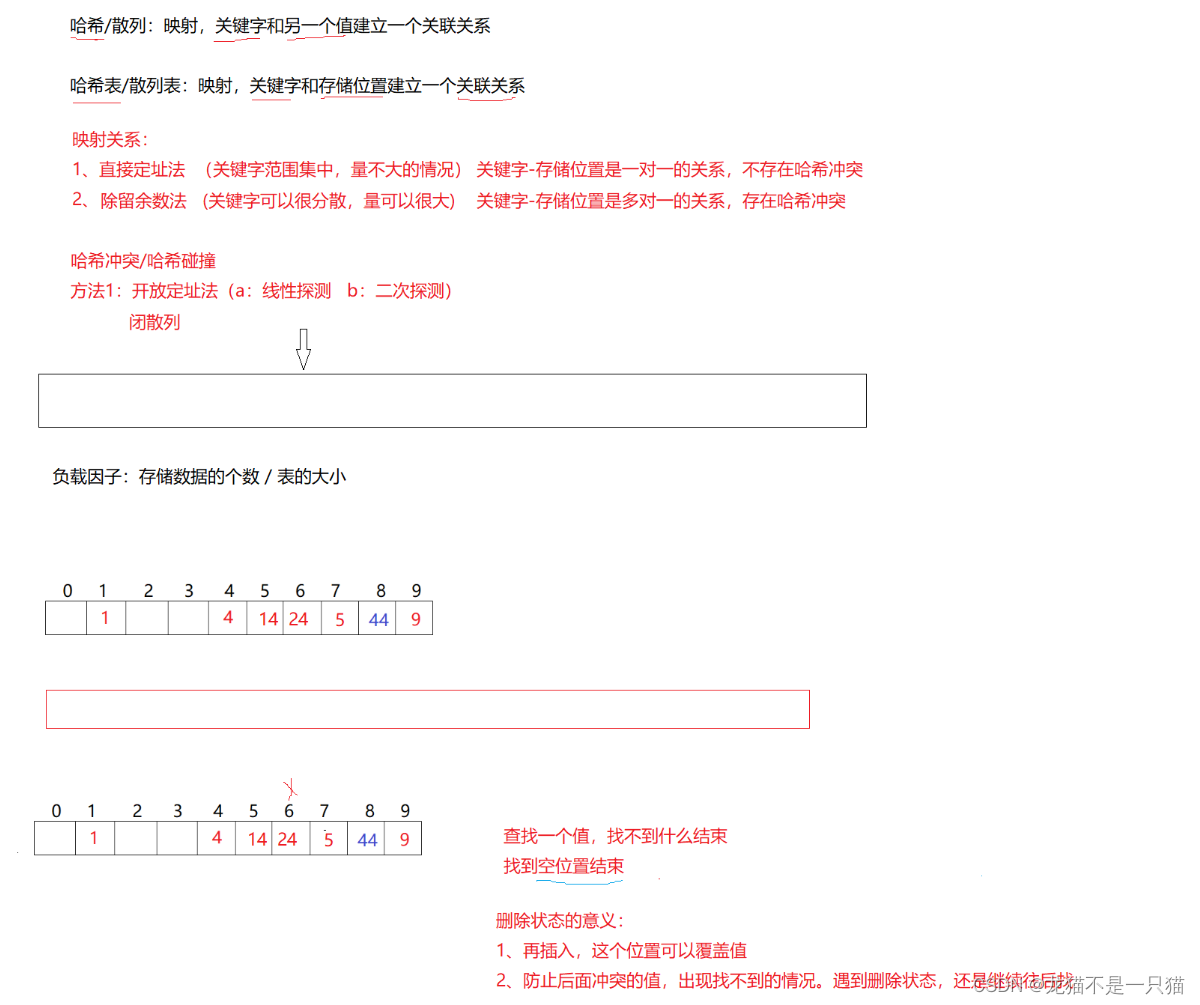
缺点：值很分散，直接定址会导致空间开很大，浪费。

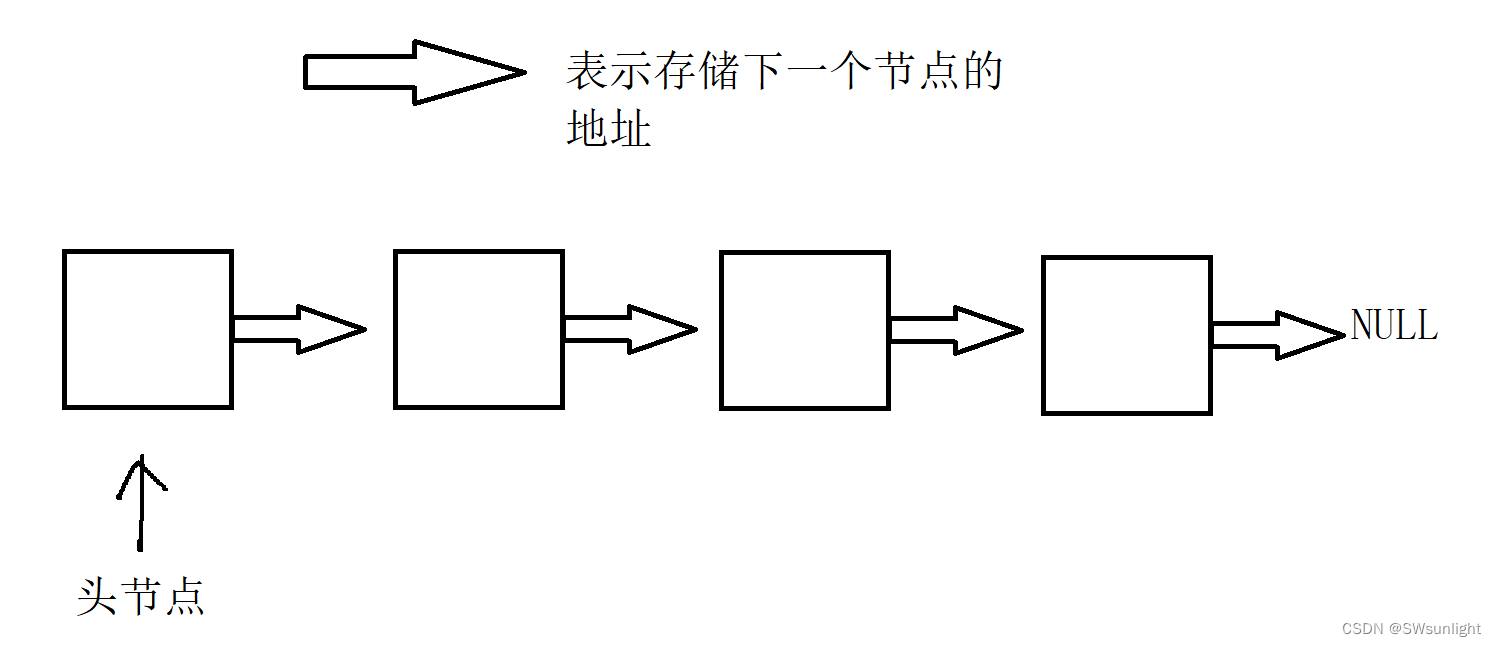
2.2开散列（哈希桶/拉链法）

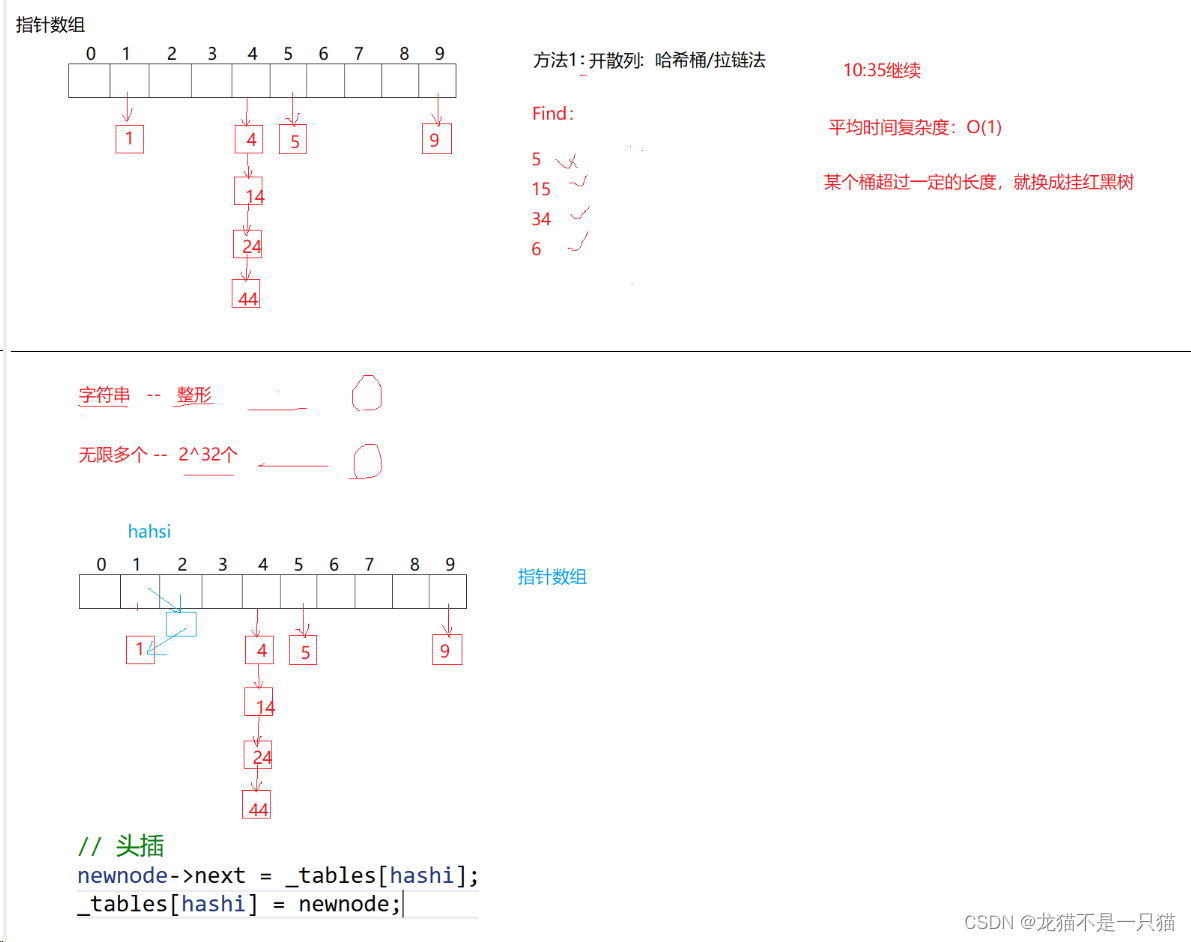
除留余数法会发生哈希碰撞（关键字可以很分散，量可以很大，关键字-存储位置是多对一的关系，存在哈希冲突）：不同的值映射到相同的位置上去。
负载因子（存储数据的个数/表的大小，也就是空间的占用率）：存储关键字的个数/空间大小

三、闭散列代码（除留余数法）

#pragma once
#include<iostream>
#include<vector>
#include<string>
using namespace std;

template<class K>
struct HashFunc
{
	size_t operator()(const K& key)
	{
		return key;
	}
};


template<>
struct HashFunc<string>
{
	size_t operator()(const string& kv)
	{
		size_t hashi = 0;
		for (auto e : kv)
		{
			hashi *= 31;
			hashi += e;
		}
		return hashi;
	}
};


namespace close
{
	enum Status
	{
		EMPTY,
		EXIST,
		DELETE
	};

	template<class K,class V>
	struct HashData
	{
		pair<K, V> _kv;
		Status _s;//表示状态
	};

	template<class K,class V,class Hash = HashFunc<K>>
	class HashTable
	{
	public:
		typedef HashData<K, V> data;
		HashTable()
		{
			_tables.resize(10);
		}

		data* find(const K key)
		{
			size_t hash = key % _tables.size();
			while (_tables[hash]._s!=EMPTY)
			{
				if (_tables[hash]._s == EXIST && _tables[hash]._kv.first == key)
					return &_tables[hash];
				hash++;
				hash %= _tables.size();
			}
			return nullptr;
		}


		bool insert(const pair<K,V>& kv)
		{
			Hash hf;
			
			if (find(kv.first))
				return false;

			if (_n * 10 / _tables.size() == 7)
			{
				//建新表
				HashTable<K,V,Hash> newtable;
				newtable._tables.resize(_tables.size() * 2);
				for (size_t i = 0; i < _tables.size(); i++)
				{
					if (_tables[i]._s == EXIST)
						newtable.insert(_tables[i]._kv);
				}
				_tables.swap(newtable._tables);
			}

			size_t hash = hf(kv.first) % _tables.size();
			//线性探测
			while (_tables[hash]._s != EMPTY)
			{
				hash++;
				hash %= _tables.size();
			}
			_tables[hash]._kv = kv;
			_tables[hash]._s = EXIST;
			_n++;
			return true;
		}

		bool erase(const K& key)
		{
			data* ret = find(key);
			if (ret)
			{
				_n--;
				ret->_s == DELETE;
				return true;
			}
			return false;
		}

		void Print()
		{
			for (size_t i = 0; i < _tables.size(); i++)
			{
				if (_tables[i]._s == EXIST)
				{
					//printf("[%d]->%d\n", i, _tables[i]._kv.first);
					cout << "[" << i << "]->" << _tables[i]._kv.first << ":" << _tables[i]._kv.second << endl;
				}
				else if (_tables[i]._s == EMPTY)
				{
					printf("[%d]->\n", i);
				}
				else
				{
					printf("[%d]->D\n", i);
				}
			}

			cout << endl;
		}


	private:
		vector<data> _tables;
		size_t _n = 0;
	};

}

四、开散列代码（拉链法/哈希桶）

namespace hash_bucket
{
	template<class K,class V>
	struct HashNode
	{
		pair<K, V> _kv;
		HashNode<K, V>* _next;
	};

	template<class K,class V,class Hash = HashFunc<K>>
	class HashTable
	{
	public:
		typedef HashNode<K, V> Node;
		HashTable()
		{
			_tables.resize(10, nullptr);
		}

		~HashTable()
		{
			for (size_t i = 0; i < _tables.size(); i++)
			{
				Node* cur = _tables[i];
				if (cur)
				{
					Node* next = cur->_next;
					delete cur;
					cur = next;
				}
				_tables[i] = nullptr;
			}
		}

		Node* find(const K& key)
		{
			Hash hf;
			size_t hash = hf(key) % _tables.size();
			Node* cur = _tables[hash];
			while (cur)
			{
				if (hf(cur->_kv.first) == hf(key))
					return cur;
				cur = cur->_next;
			}
			return nullptr;
		}


		bool insert(pair<K,V>& kv)
		{
			Hash hf;
			if (find(kv.first))
				return false;

			if (_bucket == _tables.size())
			{
				HashTable newtable;
				newtable._tables.resize(_tables.size() * 2, nullptr);
				for (size_t i = 0; i < _tables.size(); i++)
				{
					Node* cur = _tables[i];
					while (cur)
					{
						size_t hash = hf(cur->_kv.first) % newtable._tables.size();
						cur->_next = newtable._tables[hash];
						newtable._tables[hash] = cur;
						cur = cur->_next;
					}
				}
				_tables.swap(newtable._tables);
			}

			size_t hash = hf(kv.first) % _tables.size();
			Node* cur = new Node(kv);
			cur->_next = _tables[hash];
			_tables[hash] = cur;
			_bucket++;
			return true;
		}

		bool erase(const K& key)
		{
			Hash hf;
			size_t hash = hf(key) % _tables.size();
			Node* cur = _tables[hash];
			Node* prev = nullptr;
			while (cur)
			{
				if (hf(key) == hf(_tables[hash]->_kv.first))
				{
					_tables[hash] = cur->_next;
					delete cur;
					return true;
				}
				else
				{
					if (hf(key) == hf(cur->_kv.first))
					{
						prev->_next = cur->_next;
						delete cur;
						return true;
					}
					prev = cur;
					cur = cur->_next;
				}
			}
			_bucket--;
			return false;
		}

	private:
		vector<Node*> _tables;
		size_t _bucket = 0;
	};

}

代码解读：这里的插入节点是头插（效率高一些）