pnpm与npm的区别
PNPM和NPM是两个不同的包管理工具。
NPM(Node Package Manager)是Node.js的官方包管理工具,用于安装、发布和管理Node.js模块。NPM将包安装在项目的node_modules目录中,每个包都有自己的依赖树。
PNPM(Plug’n’Play Package Manager)是一个新的包管理工具,也是NPM的另一个替代方案。与NPM不同,PNPM使用符号链接(symlink)而不是复制文件来安装包。这意味着所有的包都被安装在一个共享的存储库中,并且可以在不同的项目之间共享。这样可以显著减少磁盘使用量,并加快安装和更新过程。
除了安装方式的不同,PNPM还具有一些其他的特性,如并行安装、快速执行等。然而,由于PNPM是相对较新的工具,它可能不太稳定,并且与某些包可能存在兼容性问题。
总而言之,PNPM是一种替代NPM的包管理工具,它使用符号链接来安装包,从而提供更快的安装和更新速度,并节省磁盘空间。然而,由于其相对较新和不稳定的性质,开发人员需要权衡使用PNPM的风险和优势。
pnpm 存储依赖的路径,可以使用 pnpm 的 store 配置选项。
通过更改 store 配置,可以指定 pnpm 存储依赖的目录位置。这在希望将依赖存储在不同磁盘分区、不同的硬盘驱动器或其他自定义位置时很有用。
pnpm修改默认包的存储路径
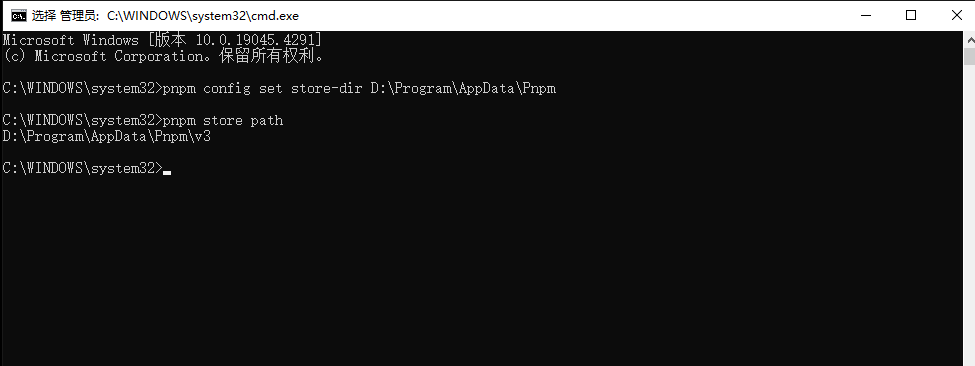
1.以管理员身份打开CMD命令行
2.运行以下命令设置新的存储路径(path路径不能为中文)
pnpm config set store-dir <new path>
3.输入命令验证是否修改成功
pnpm store path
如图所示